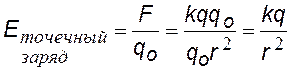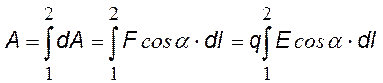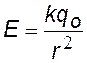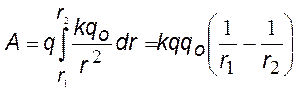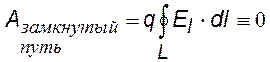Книга по электромагнетизму
ЭЛЕКТРОСТАТИКА
Электрический заряд – это свойство некоторых частиц, характеризующее их способность к особому типу взаимодействия, называемому электромагнитным взаимодействием. [1] Что нам известно об электрических зарядах?
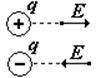
1) Различают заряды двух типов – положительные и отрицательные.
2) Разноименные заряды притягиваются, одноименные – отталкиваются.
3) Наименьший отрицательный заряд – это заряд электрона (е = 1,6×10-19Кл), положительный — протона (+е). Заряды любых тел всегда дискретны и кратны заряду электрона. Так как число заряженных частиц в телах огромно, а размеры частиц очень малы, в большинстве случаев можно говорить о непрерывном распределении зарядов в телах. [2]
4) Закон сохранения электрического заряда: «В замкнутой (электрически изолированной) системе суммарный заряд остается постоянным».
5)Электрический заряд является инвариантом, иначе говоря, величина заряда остается одной и той же, независимо от того, движется он в какой либо системе отсчета или покоится.
Электростатическое поле в вакууме. [3]
Закон Кулона [4] : сила электростатического взаимодействия между двумя заряженными сферами (шарами) прямо пропорциональна величинам их зарядов и обратно пропорциональна квадрату расстояния между их центрами. В общем случае кулоновская сила – это двойной векторный интеграл, который можно взять только в некоторых простейших случаях.
|
|
Кулоновская (электростатическая) сила. В таком виде закон Кулона применим только для двух точечных зарядов, сфер (шаров), r – расстояние между центрами сфер (шаров). |
|
|
|
|
|
eо » 8,85×10-12 (Кл2/Н. м2) – электрическая постоянная |
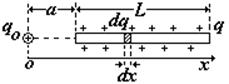
В качестве примера вычисления кулоновского взаимодействия заряженных тел рассмотрим силу, с которой действует тонкий стержень длиной L, заряженный с линейной плотностью заряда t (Кл/м) , на точечный заряд qо, находящийся на расстоянии а от конца стержня. (см. рис.). (Полем на концах стержня пренебрегаем)
|
|
выделим в стержне элементарный заряд dq, |
|
|
|
сила взаимодействия между зарядом qо и элементарным зарядом dq стержня |
|
|
|
сила взаимодействия между стержнем и точечным зарядом |
|
Заряды, сообщаемые телам, распределяются неравномерно. В металлах заряды распределяются всегда по поверхности; в тех местах, где кривизна поверхности большая, там больше скапливается зарядов (см. дальше). Для характеристики распределения зарядов используются:
|
|
линейная плотность заряда — эта заряд, приходящийся на единицу длины заряженного тела. |
|
|
поверхностная плотность заряда – это заряд, приходящийся на единицу площади поверхности заряженного тела |
|
|
объемная плотность заряда – это заряд, приходящийся на единицу объема заряженного тела |
Электростатика изучает электрические поля, создаваемые заряженными телами, в которых распределение зарядов не меняется с течением времени. В электростатике используется модель – точечный заряд – это заряженное тело, размерами которого можно пренебречь по сравнению с другими размерами в данной задаче. Кроме того, вводится понятие – пробный заряд – это заряд, вносимый в поле другого заряженного тела, и при этом не влияющий на это поле. Это можно перефразировать (не очень научно) так: один заряд создает поле, а другой в этом поле находится и не влияет на поле. Именно такой подход используется при решении большинства задач. [5]
Вокруг заряженных тел существует электрическое поле, которое характеризуют напряженностью Е и потенциалом j (см. ниже).
|
|
напряженность (вектор) – силовая характеристика электрического поля, по смыслу – это сила, действующая на единичный положительный пробный заряд в данной точке поля. |
|
|
|
Используя закон Кулона, можно найти напряженность поля точечного заряда; q заряд, создающий поле, qo — пробный заряд, вносимый в это поле. |
Работа по переносу заряда в электростатическом поле.
|
|
Сила, действующая на заряд в электрическом поле. Это выражение может быть использовано всегда, тогда как формула (·) применима только для точечных зарядов, сфер и шаров. |
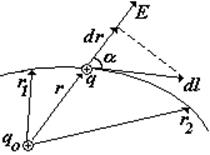
Пусть точечный заряд q переносится в поле, создаваемом другим точечным зарядом qо. Найдем работу, необходимую для переноса q из положения с радиус-вектором r1 в положение с радиус-вектором r2. (см. рис.).
|
|
полная работа по переносу заряда q в электрическом поле, a — угол между вектором Е и вектором перемещения dl |
|
|
|
Сведем подынтегральное выражение к одной переменной r, используя выражение для напряженности поля заряда qо и связь между перемещением dl и приращением радиус-вектора dr. Интегрируя, найдем выражение для работы. |
|
|
|
Из этой формулы следует очень важный вывод: работа в электростатическом поле не зависит от формы пути, а определяется только начальным и конечным положением переносимого заряда. |
|
|
Работа в электростатическом поле по замкнутому пути равна нулю |
Из механики известно, что силовое поле, работа в котором определяется только начальным и конечным положениями тела, называется консервативным. Следовательно, электростатическое поле является консервативным или чаще говорят, потенциальным Линейный интеграл по замкнутому контуру L называется циркуляцией. Отсюда следует:
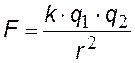 (·)
(·)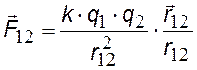
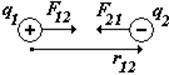 векторная форма, знак силы (±) зависит от выбора направления радиус-вектора
векторная форма, знак силы (±) зависит от выбора направления радиус-вектора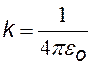
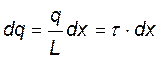
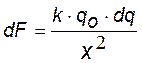
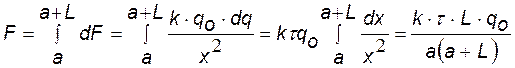
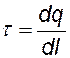 (Кл/м)
(Кл/м)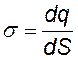 (Кл/м2)
(Кл/м2)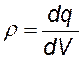 (Кл/м3)
(Кл/м3)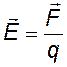 (Н/Кл=В/м)
(Н/Кл=В/м)