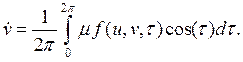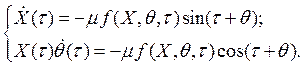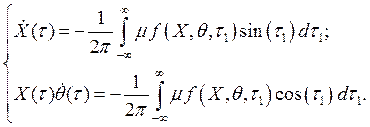Линейный контур с затуханием
(3.1)
Введём так называемую функцию диссипации
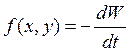 .
.
Теперь продифференцируем уравнение (3.1) по времени, тогда
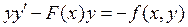 или
или 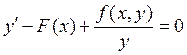 .
.
Это уравнение по сути дела есть уравнение закона Ньютона: ускорение равняется действующей силе. Здесь F(x) — потенциальная сила, зависящая от координаты, а f(x, y)/y — сила трения, зависящая от скорости.
В физически реализуемых колебательных системах диссипация всегда связана с движением. Для покоящегося тела диссипации быть не должно, т. е. f(x, y)/y ® 0 при y ® 0. Мы сказали, что для диссипативных систем dW/dt < 0, а это значит, что функция f(x, y) > 0. Следовательно, функция f(x, y)/y имеет знак совпадающий со знаком y.
Наличие диссипации в системе изменяет характер особых точек. Если для математического маятника особыми точками были центр и седло, то для диссипативных систем вместо центра появляются фокус или узел, в зависимости от величины диссипации.
Для анализа систем с малыми диссипациями и малыми нелинейностями существуют специальные приближённые методы, в частности, метод медленно меняющихся амплитуд. Рассмотрим этот метод на задачах, имеющих аналитическое решение (чтобы было с чем сравнивать), а потом уже будем применять там, где нет аналитических решений.
3.1. Линейный контур с затуханием
|
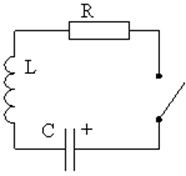
Рассматриваем RLC колебательный контур — простейшая система с затуханием. Мы зарядили конденсатор, и в момент времени t0 замкнули ключ (рис. 22). Уравнение колебаний в такой системе: |
Рис. 22. Линейный контур с затуханием. |
|
|
(3.2) |
|
Точка равновесия x = 0 представляет собой устойчивый фокус. Найдём уравнение фазовых траекторий. Для этого преобразуем это уравнение стандартным образом:
|
|
Откуда просто получаем уравнение фазовых траекторий
|
|
(3.3) |
Это уравнение не очень удобно, так как в правой части зависит как от x, так и от y, поэтому введём новую переменную z = y/x, тогда (3.3) перепишем в виде
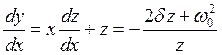 .
.
Выполним некоторые элементарные преобразования:
 ,
,
или, проинтегрировав,
 ;
;
мы обозначили ![]() . Запишем z через x и y, и возведём в exp:
. Запишем z через x и y, и возведём в exp:
|
|
(3.4) |
У нас получились уравнение фазовой траектории в явном виде. Придадим этому уравнению более удобную форму. Для этого введём ещё одни новые переменные u = y + dx, v = wx. Если w0 > d (затухание мало), то w действительное число, тогда (3.4) принимает вид:
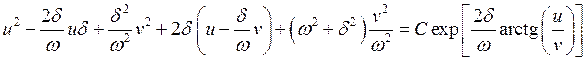 .
.
Перейдём к полярным координатам: v = rcosj, u = rsinj, тогда
|
|
(3.5) |
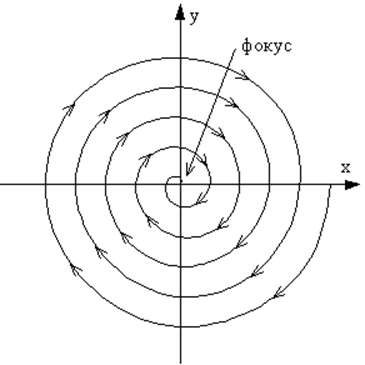
Интегральная кривая соответствующая этому случаю изображена на рис. 23.
Если затухание велико, т. е. w0 < d, тогда w2 отрицательное, и w — мнимое число (w = iq). Опять, путём несложных преобразований, получим уравнение
|
|
(3.6) |
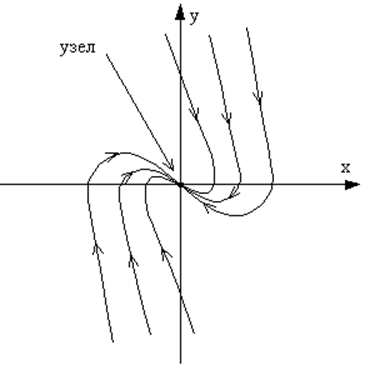
Фазовый портрет для этого случая показан на рис. 24.
|
Рис. 23. Фазовый портрет системы с затуханием меньше критического. |
Рис. 24. Фазовый портрет системы с затуханием больше критического. |
При w0 > d мы имеем дело с затухающими колебаниями линейного осциллятора, фазовый портрет которых представляет собой совокупность спиралей, стягивающихся в особую точку типа фокус. Для w0 < d система становится апериодической, и на фазовой плоскости движения изображаются фазовыми траекториями, имеющими вид кривых, сходящихся в особую точку типа узел без обхода вокруг неё. В обоих случаях в диссипативных системах особые точки (фокус и узел) устойчивы и соответствуют единственному положению равновесия системы — состоянию покоя, к которому система приходит из любых начальных условий, при любом начальном смещении или скорости.
3.2. Метод медленно меняющихся амплитуд, укороченные уравнения
Вопрос 7
Метод медленно меняющихся амплитуд (ММА) применим к системам с малыми нелинейностью и диссипацией и основан на известной теореме, что свойства системы и решение описывающего её ДУ изменяются непрерывно при изменении параметров этого уравнения. При малых нелинейностях и диссипации движение в системе будет близко к чисто гармоническому, соответствующему линейной консервативной системе, уравнение которой имеет вид
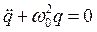 .
.
Введём безразмерное время t = w0t, тогда в этом масштабе времени уравнение будет таким
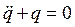 .
.
Для системы близкой к линейной консервативной уравнение выглядит так:
|
|
(3.7) |
где f — произвольная регулярная, в общем случае нелинейная функция координаты q и скорости её изменения, значения которой остаются малыми по сравнению со значениями членов, стоящих в левой части уравнения (3.7) (в силу слабой нелинейности параметров и малых потерь в системе).
Выберем в уравнении (3.7) масштаб по координате q и перейдём к безразмерной переменной x так, чтобы при колебаниях изменение x было порядка единицы, тогда правая часть (3.7) должна быть много меньше единицы:
|
|
(3.8) |
При m = 0 решением уравнения будут чисто гармонические колебания
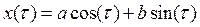 ,
,
где a и b — постоянные, задаваемые начальными условиями.
При 0 < |m| < 1 будем считать, что решение может быть записано в виде
|
|
(3.9) |
где u(t) и v(t) — медленно меняющиеся функции (в сравнении с cos(t)), так что
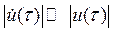 ,
, 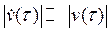 .
.
Но получается, что одной функции x(t) ставятся в соответствие две функции u(t) и v(t), т. е. задача становится заведомо неоднозначной. Можно произвольно задать одну из функций и подобрать к ней вторую, при этом, если мы не угадаем, то эта функция будет быстро меняться. Потребуем, чтобы функция x(t) удовлетворяла условию:
|
|
(3.10) |
для чего необходимо и достаточно, чтобы
|
|
(3.11) |
При выполнении условия (3.11) уравнение-связь (3.9) становится однозначным, т. е. становится однозначной связь функций x(t), u(t) и v(t).
Используя уравнения (3.9) — (3.11), преобразуем (3.8): продифференцируем (3.10) по времени и сложим с (3.9) с учётом (3.8):
|
|
(3.12) |
Умножим (3.12) на sin(t), а (3.11) на cos(t) и вычтем из первого второе; потом умножим (3.12) на cos(t), а (3.11) на sin(t) и сложим их, тогда получим систему:
|
|
(3.13) |
Таким образом, мы получили систему двух уравнений первого порядка (3.13), которая, естественно, полностью эквивалентна одному уравнению второго порядка (3.8). Она не даёт никаких преимуществ в смысле упрощения задачи. Существенный в шаг в сторону нахождения приближенного решения можно сделать, если воспользоваться условием медленного изменения функций u и v за период. Заменим мгновенные значение u и v их средними значениями за каждый период колебаний, равный 2p. Производя усреднение по периоду, мы приходим к системе так называемых укороченных уравнений
|
|
(3.14) |
Эта система уже не содержит в правой части в явном виде времени t, и во многих случаях её можно легко проинтегрировать, получая временной ход медленно меняющихся функций u(t) и v(t), являющихся амплитудами искомого решения.
Систему уравнений (3.14) можно получить из системы (3.13), если правые
части разложить в ряд Фурье как периодические функции с периодом 2p и отбросить все осциллирующие члены (в системе (3.14) записаны только первые слагаемые ряда). В этом отбрасывании осциллирующих членов и заключается "укорочение", приводящее от системы уравнений, точно соответствующей исходному уравнению, к приближенным укороченным уравнениям.
Переход от переменных x, ![]() к переменным u, v эквивалентен переходу от фазовых координат x,
к переменным u, v эквивалентен переходу от фазовых координат x, ![]() к вращающейся системе координат u, v. Это означает, что система координат u, v в координатной плоскости x,
к вращающейся системе координат u, v. Это означает, что система координат u, v в координатной плоскости x, ![]() вращается с угловой частотой, равной единице.
вращается с угловой частотой, равной единице.
Рассмотрим теперь другой вариант метода ММА с переходом от исходных координат x, ![]() к радиальным координатам — амплитуде X и фазе q, которые также являются медленными переменными в масштабе времени t.
к радиальным координатам — амплитуде X и фазе q, которые также являются медленными переменными в масштабе времени t.
Будем теперь искать решение исходного уравнения (3.8) в виде
|
|
(3.15) |
Введём замену переменной ![]() :
:
|
|
(3.16) |
для чего необходимо положить
|
|
(3.17) |
Дальше дифференцируем (3.16) по времени, с учётом равенства (3.17), и вместе с (3.15) подставляем в исходное уравнение (3.8), тем самым, выражая его через новые переменные X и q.
|
|
(3.18) |
Из (3.17) и (3.18) находим точную систему дифференциальных уравнений, описывающих процессы в системе
|
|
(3.19) |
Здесь X(t) и q(t) являются медленными функциями времени t, что позволяет усреднить правые части (3.19) за период, считая, что за это время X и q не меняются. Указанная процедура усреднения приводит к системе укороченных уравнений вида
|
|
(3.20) |
Мы обозначили t1 = t + q.
Найдём спектр ММА колебания. Для этого запишем сигнал ММА (3.15) в реальном масштабе времени:
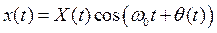 .
.
Предполагается, что соотношение (3.16) выполняется, а центральная частота w0 выбирается так, чтобы амплитуда колебаний X(t) менялась как можно медленнее. Условие медленного изменения амплитуды принимает вид:
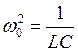 ,
, 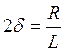 .
.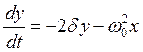 ,
, 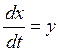 .
. .
.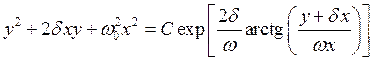 .
.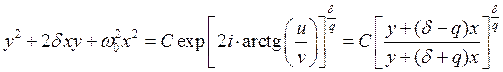 .
.

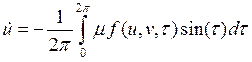 ;
;