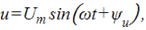Представление синусоидальных функций в различных формах
Задача 3.4.
Определить частоту синусоидального тока
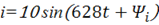 .
.
3.2. Представление синусоидальных функций в различных формах (аналитическое, при помощи векторов и при помощи комплексных чисел).
Аналитическое представление синусоидальных функций неудобно для расчета электрических цепей, так как алгебраические действия с тригонометрическими функциями приведет к громоздким вычислениям.
Представление синусоидальных функций при помощи векторов в прямоугольной системе координат позволяет наглядно показать количественные и фазовые соотношения в цепях синусоидального тока. В электротехнике векторы изображают неподвижными для момента времени t=0(рис. 3.3) и их масштабы выбирают так, чтобы длина вектора соответствовала действующему значению, а углы наклона к оси абцисс равны начальным фазам (ψu, ψi), при этом угловая частота ω – должна быть известна.
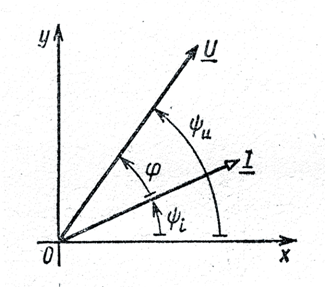
Рис. 3.3
Угол между векторами равен углу сдвига фаз φ= ψu — ψi. Если ψu> ψi, то φ > 0 и напряжение опережает ток по фазе, в противном случае φ < 0 и напряжение отстает по фазе от тока. Угол φ всегда откладывается от вектора I к вектору U.
Для представления синусоидальных функций при помощи комплексных чисел используются комплексные плоскости с осями координат +1 – ось положительных действительных чисел и величин и +j – ось положительныхмнимых чисел и величин (рис. 3.4). На этой плоскости откладывается вектор I длиной I (действующее значение тока) под углом ψi к действительной оси. Его проекцию на ось действительных чисел обозначают I/ , на ось мнимых чисел I// . Тогда вектор I в комплексном виде запишется:
I = I/ +jI// .
Такая форма записи комплексного числа называется алгебраической.
Из рис. 3.4 Следует, что I/ = ICosψi, I// = ISinψi , поэтому вектор можно записать и в тригонометрической форме:
I = I Cos ψi + jISinψi.
Если принять во внимание формулу Эйлера 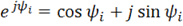 , тот же вектор I можно записать в показательной форме:
, тот же вектор I можно записать в показательной форме:
I = Iejψi.
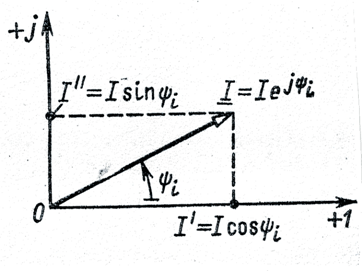
Рис. 3.4
Переход от алгебраической формы записи к тригонометрической и показательной выполняется по формулам:
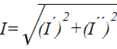 ;
;
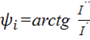 , при
, при![]() >0 ;
>0 ;
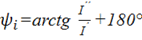 , при
, при![]() < 0.
< 0.
При сложении и вычитании комплексных чисел или величин используют алгебраическую форму записи, при умножении, делении, логарифмировании предпочтение отдают показательной форме записи числа и величин.
3.3. Основные элементы цепи синусоидального тока (цепь с резистивным элементом, цепь с индуктивным элементом, цепь с емкостным элементов).
3.3.1. Цепь синусоидального тока с резистивным элементом (рис. 3.5, а)
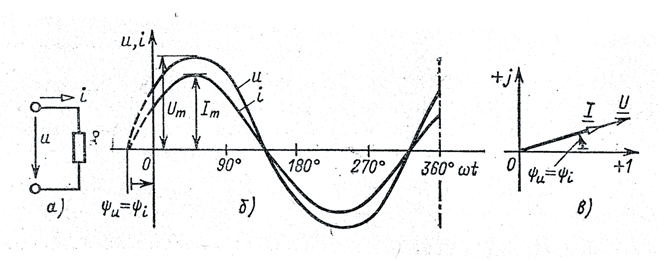
Рис 3.5
Если к резистивному элементу приложить синусоидальное напряжение u=Umsin(ωt+ψu), то по закону Ома:
i=u/R= Umsin(ωt+ψu)/R,
откуда следует, что ток тоже будет изменяться по синусоидальному закону:
i= Imsin(ωt+ψi),
где Im = Um/R,
ψi = ψu (сдвиг фаз цепи с резистивным элементом φ = ψu — ψi = 0)
(рис. 3.5, б, в).
Заменим мгновенные значения u и i комплексными выражениями в показательной форме:
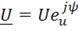 ,
, 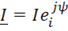
РазделивUнаI, получим
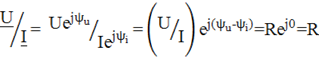
Тогда закон Ома в комплексном виде для участка цепи с резистивным элементом запишется:
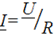 .
.
3.3.2. Цепь синусоидального тока с индуктивным элементом (рис. 3.6, а).
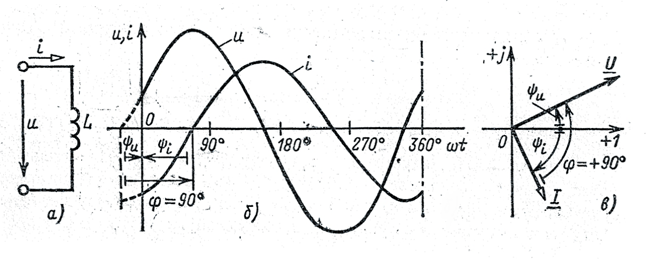
Рис. 3.6
Если к индуктивному элементу приложить синусоидальное напряжение
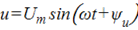 ,
,
то в катушке потечет ток, его магнитодвижущая сила iw (w – число витков катушки) вызовет магнитный поток Ф, изменяющийся тоже по синусоидальному закону. Сумма магнитных потоков, связанных с витком, называется потокосцеплением Ψ=wФ.
Потокосцепление и ток катушки в линейных электрических цепях связаны соотношением:
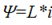 ,
,
где L — коэффициент пропорциональности — индуктивность катушки.
По закону электромагнитной индукции в катушке индуктивности индуцируется ЭДС самоиндукции
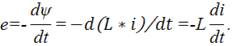
В катушке будет ток, если напряжение на её выводах компенсирует ЭДС самоиндукции, поэтому для катушки:
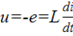 ,
,
откуда
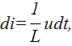
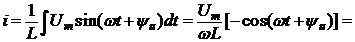
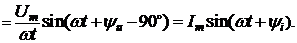
При этом постоянная интегрирования равна нулю, так как ток синусоидальный и не имеет постоянной составляющей.
Амплитуда тока 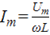 , а действующее значение
, а действующее значение![]() где ωL=XL – индуктивное сопротивление.
где ωL=XL – индуктивное сопротивление.
Начальная фаза тока 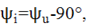 откуда сдвиг фаз
откуда сдвиг фаз 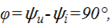
т. е. ток по фазе отстает от напряжения на 90° (рис. 3.6, б, в).
Заменим мгновенные значения тока i и напряжения u их комплексными выражениями
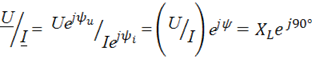 .
.
Тогда для участка цепи с индуктивным элементом закон Ома в комплексной форме запишется:
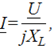
где jXL – индуктивное сопротивление в комплексной форме, представляющее собой положительное мнимое число.
3.3.3. Цепь синусоидального тока с емкостным элементом (рис.3.7, а)
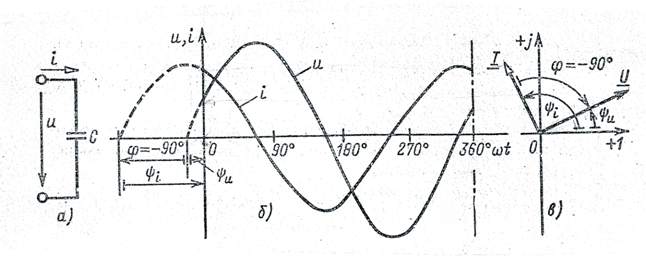
Рис. 3.7
Если к емкостному элементу приложить синусоидальное напряжение