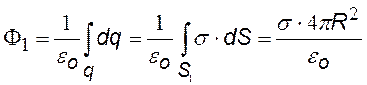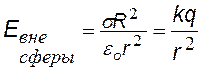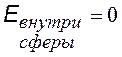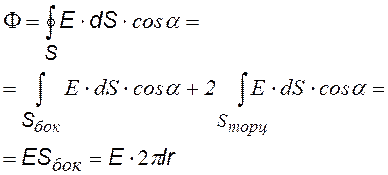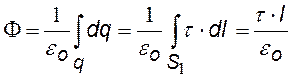Напряженность поля тонкого стержня конечной длины
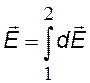
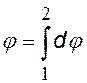
при непрерывном
распределении зарядов
В качестве примера получения выражения для напряженности поля с помощью принципа суперпозиции найдем напряженность поля тонкого стержня конечной длины, равномерно заряженного с линейной плотностью заряда t
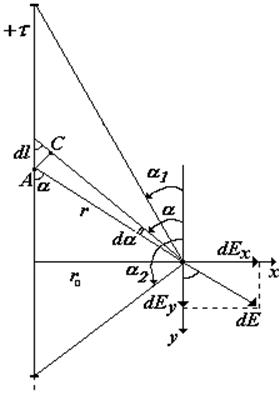
Выберем бесконечно малый элемент dl стержня с зарядом dq. Поскольку напряженности от различных элементов направлены по-разному, введем оси проекций х и у. Итегрируя, найдем результирующие напряженности Ех и Еу.
|
|
dE— напряженность от элемента стержня dl с зарядом dq = t×dl, dEх и dEy – проекции dE на направления х и у. |
|
|
|
Чтобы проинтегрировать, сведем к одной переменной a |
|
|
|
длина дуги АС при малых углах, она же из треугольника (А, С, dl) |
|
|
|
||
|
|
|
модуль напряженности |
|
|
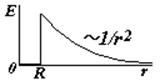
Для бесконечно длинной нити a1 ® 0, a2 ® 180о, следовательно, Еу = 0 и Е = Ех (cos180o = -1), r – расстояние от точки, в которой определяется напряженность, до нити. |
Этот пример показывает, что вычисление напряженности полей представляет собой достаточно сложную задачу даже в нашем случае, когда мы не учитывали поле вблизи концов стержня.
Основной задачей электростатики является вычисление полей заряженных тел. Найти напряженность поля заряженного тела можно с помощью:
1) принципа суперпозиции — это сложная математическая задача, решаемая только в некоторых простых случаях или
2) теоремы Гаусса, которая упрощает расчеты, но только в случае бесконечной плоскости, бесконечной нити (цилиндра) или сфер и шаров (см. ниже).
Теорема Гаусса.
Сначала введем понятие «поток вектора» — это скалярная величина
|
(Н×м2/Кл = В×м) |
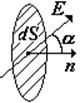
элементарный поток вектора напряженности Е, n – нормаль к площадке, dS – элементарная площадка – это такая малая площадка, в пределах которой Е = const; Еn – проекция вектора Е на направление нормали n |
|
|
|
поток вектора напряженности через конечную площадку S |
|
|
|
-²- -²- -²-через замкнутую поверхность S |
|
|
|
при дискретном распределении зарядов |
Теорема Гаусса: «Поток вектора напряженности через любую замкнутую поверхность равен алгебраической сумме зарядов, охватываемых этой поверхностью, деленной на eо» (eо – электрическая постоянная) |
|
|
при непрерывном распределении зарядов |
Применение теоремы Гаусса.
Чтобы найти напряженность с помощью теорем Гаусса, нужно взять интеграл. А как его взять, если мы Е еще только пытаемся найти? Кроме того, под интегралом «мешает» cosa. Надо суметь выбрать такую замкнутую поверхность (ее удобно называть гауссовой), в каждой точке которой было бы Е = const, и cosa = const. Тогда в левой части теоремы Е и cosa можно будет вынести из-под знака интеграла. Поэтому практически теорему Гаусса можно применить только в следующих случаях: сфера, шар, длинная нить, длинный цилиндр, бесконечная плоскость.
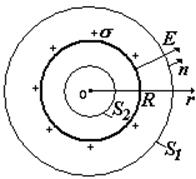
1) Сфера, заряженная с поверхностной плотностью заряда s (Кл/м2)
Рассмотрим области : 1) вне сферы (![]() ) и внутри ее (
) и внутри ее ( ). Выберем поверхности: 1) S1 и 2) S2 – обе поверхности – сферы, концентрические с заряженной сферой. Сначала найдем потоки вектора Е через выбранные поверхности, а затем воспользуемся теоремой.
). Выберем поверхности: 1) S1 и 2) S2 – обе поверхности – сферы, концентрические с заряженной сферой. Сначала найдем потоки вектора Е через выбранные поверхности, а затем воспользуемся теоремой.
|
|
Потоки вектора Е через S1 ( E^n, a = 0, cosa = 1. |
|
|
|
по теореме Гаусса; F2 = 0, т. к. S2 не охватывает никаких зарядов. Приравнивая потоки из (¨) и (¨¨), найдем E(r). |
|
|
|
||
|
q = s×2pR2 – полный заряд сферы |
Вне сферы поле такое же, как поле точечного заряда. На границе сферы происходит скачок напряженности. |
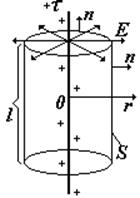
2)Тонкая длинная нить, заряженная с линейной плотностью заряда t (Кл/м)
В этом случае «гауссова» поверхность – соосный с нитью цилиндр длиной l.
Сначала найдем поток, потом воспользуемся теоремой Гаусса.
|
|
Разобьем поверхность цилиндра на боковую и две торцевых. Для боковой — cosa = 1, для торцевых — cosa = 0. |
|
|
|
Рефераты по физике сдают здесь
Другие статьиПохожая информацияУзнать стоимость за 15 минут
Распродажа дипломных
Подпишись на наш паблик в ВК
Нужна работа?
|
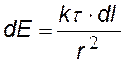
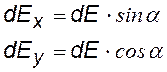
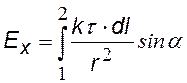
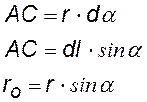
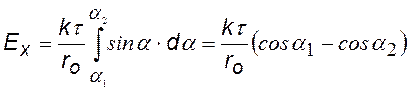
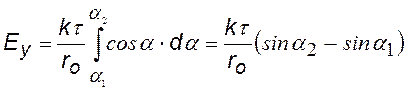
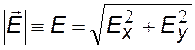
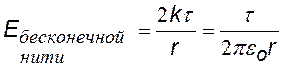
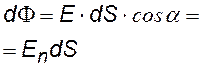
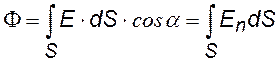
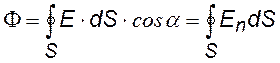
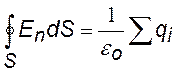
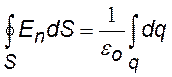
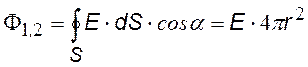 (¨)
(¨)