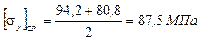Определение положения центра тяжести сложного сечения
4) Сравним веса валов
Найдем площадь поперечного сечения для каждого из валов: круглого, кольцевого, прямоугольного.
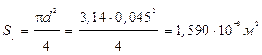
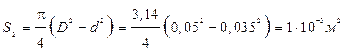
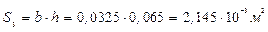
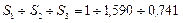
Указания к задаче 5
Определение положения центра тяжести сложного сечения
Координаты центра тяжести любой сложной фигуры можно определить по формулам:
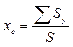 ,
, 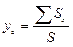 ,
,
где Sx, Sy – статические моменты площади сечений простых фигур, составляющих сложную фигуру;
S – площадь фигуры.
Сумма статических площадей простых фигур определяется по формуле:
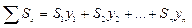 ,
, 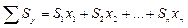 ,
,
где Si – площадь i-той простой фигуры;
xi, yi – координаты центра тяжести i-той простой фигуры.
ПРИМЕР 1
Определить положение центра тяжести фигуры, показанной на рис. 10.
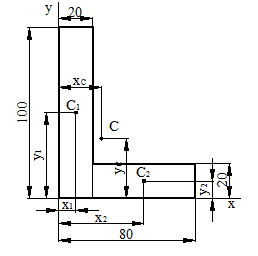
Рисунок 10.
1) Выбираем произвольные оси координат
2) Разбиваем сечение на простейшие фигуры
3) Находим площадь каждой из фигур
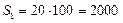 мм2;
мм2;
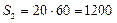 мм2.
мм2.
4) Определяем статические моменты площади
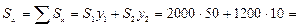
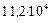 мм3
мм3
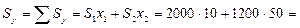
![]() мм3
мм3
5) Находим координаты центра тяжести
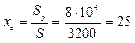 мм;
мм;
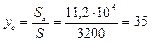 мм.
мм.
Определение моментов инерции сечения при параллельном переносе осей
Пусть известны все геометрические характеристики сечения относительно исходных осей х, у (рис. 11). Определим моменты инерции относительно параллельных им осей хС, уС, проходящих через центр тяжести сечения.
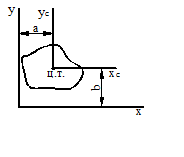 |
Рисунок 11.
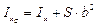 ,
,
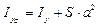 ,
,
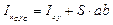 ,
,
где Ix, Iy – осевые моменты инерции относительно исходных осей;
Ixy – центробежный момент инерции относительно исходных осей;
Ixc, Iyc – осевые моменты инерции относительно центральных осей;
Ixcyc – центробежный момент инерции относительно центральных осей;
a, b – расстояние между осями.
Определение моментов инерции сечения при повороте осей
Известны все геометрические характеристики сечения относительно центральных осей хС, уС (рис. 12). Определим моменты инерции относительно осей х1, у1, повернутых относительно центральных на некоторый угол a.
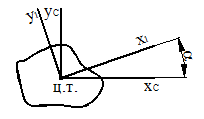
Рисунок 12.
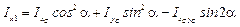 ,
,
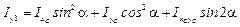 ,
,
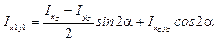 ,
,
где Ix1, Iy1 – осевые моменты инерции относительно осей х1, у1;
Ix1y1 – центробежный момент инерции относительно осей х1, у1.
Определение положения главных центральных осей инерции
Положение главных центральных осей инерции сечения определяется по формуле:
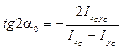 ,
,
где a0 – угол между центральными и главными осями инерции.
Определение главных моментов инерции
Главные моменты инерции сечения определяются по формуле:
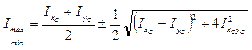
Последовательность расчета сложного сечения
1) Разбить сложное сечение на простейшие геометрические фигуры [S1, S2,…;x1, y1; x2, y2, …]
2) Выбрать произвольные оси XOY.
3) Определить положение центра тяжести сечения [xc, yc].
4) Провести центральные оси XcOYc.
5) Вычислить моменты инерции Ixc, Iyc, используя теорему параллельного переноса осей.
6) Вычислить центробежный момент инерции Ixcyc.
7) Определить положение главных осей инерции tg2a0.
8) Вычислить главные моменты инерции Imax, Imin.
ПРИМЕР 2
Для фигуры, показанной на рисунке 13 определить главные моменты
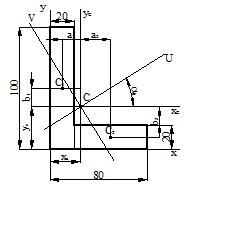
Рисунок 13.
инерции и положение главных осей инерции.
1) Разбиваем сложное сечение на простейшие геометрические фигуры
S1 = 2000 мм2, S2 =1200 мм2, S = 3200 мм2.
2) Выбираем произвольные оси XOY.
3) Определяем положение центра тяжести сечения
xc = 25 мм, yc =35 мм.
4) Проводим центральные оси XcOYc
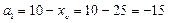 мм,
мм,
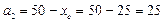 мм,
мм,
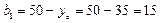 мм,
мм,
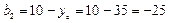 мм.
мм.
5) Вычисляем моменты инерции Ixc, Iyc
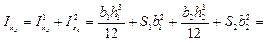
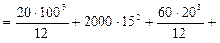
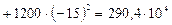 мм4
мм4
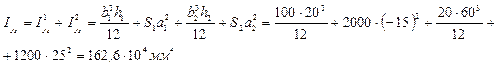
6) Вычисляем центробежный момент инерции Ixcyc
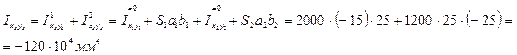
7) Определяем положение главных осей инерции
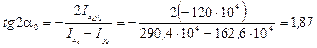
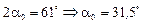
Если Ix>Iy и a0>0, то угол a0 откладывается от оси Хс против часовой стрелки.
8) Вычисляем главные моменты инерции Imax, Imin
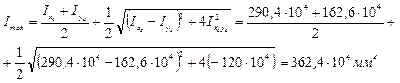
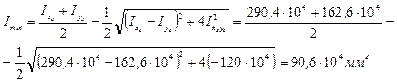
ПРИМЕР 3
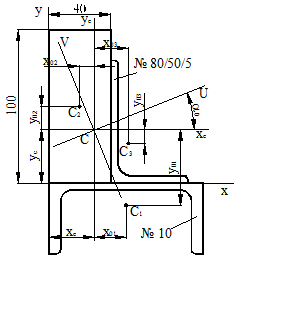 |
Для фигуры, показанной на рис. 14 определить положение главных осей
Рисунок 14.
инерции и главные моменты инерции.
1) Выписываем основные исходные данные для каждой фигуры
 Швеллер
Швеллер
S1 = 10,9 см2
Ix = 20,4 см4
Iy = 174 см4
y0 = 1,44 см
h = 10 см
 Неравнополочный уголок
Неравнополочный уголок
S3 = 6,36 см2
Ix = 41,6 см4
Iy = 12,7 см4
Imin = 7,58 см4
tga = 0,387
x0 = 1,13 см
y0 = 2,6 см
Прямоугольник
S2 = 40 см2
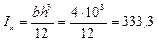 см4
см4
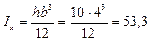 см4
см4
2) Вычерчиваем сечение в масштабе
3) Проводим произвольные оси координат
4) Определяем координаты центра тяжести сечения
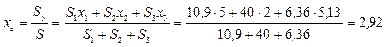 см;
см;
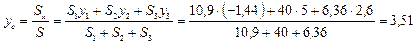 см.
см.
5) Проводим центральные оси
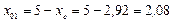 см,
см, 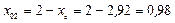 см,
см,
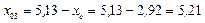 см,
см,
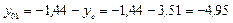 см,
см, 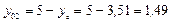 см,
см,
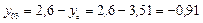 см.
см.
6) Определяем осевые моменты инерции относительно центральных осей
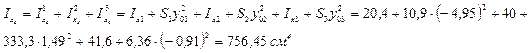
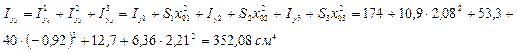
7) Определяем центробежный момент инерции относительно центральных осей
Центробежный момент инерции для угловой прокатной стали относительно ее центра тяжести определяется по одной из следующих формул:
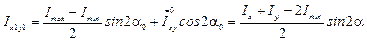
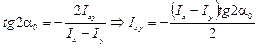
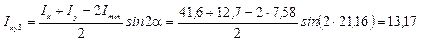 см4.
см4.
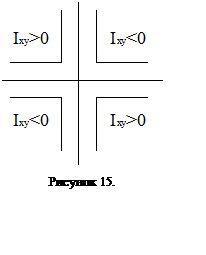
Знак центробежного момента инерции для угловой прокатной стали определяется согласно рис. 15, поэтому Ixy3 = -13,17 см4.
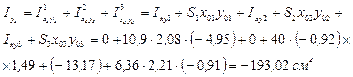
8) Определяем положение главных осей инерции
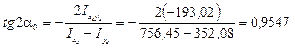
 |
a0 = 21,84°
9) Определяем главные моменты инерции
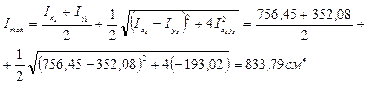
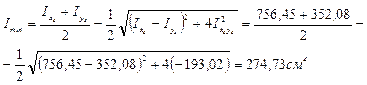
Указания к задаче 6
Изгибом называется такой вид деформации, при котором в поперечном сечении стержня возникает В. С.Ф. – изгибающий момент.
Для того, чтобы произвести расчет балки на изгиб, необходимо знать величину наибольшего изгибающего момента М и положение сечения, в котором он возникает. Точно также, надо знать и наибольшую поперечную силу Q. Для этой цели строят эпюры изгибающих моментов и поперечных сил. По эпюрам легко судить о том, где будет максимальное значение момента или поперечной силы. Для определения величин М и Q используют метод сечений. Рассмотрим схему, показанную на рис. 16. Составим сумму сил на ось Y, действующих на отрезанную часть балки.
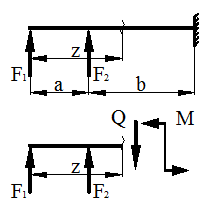 |
Рисунок 16.
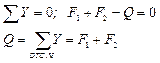
Поперечная сила равна алгебраической сумме всех сил, действующих по одну сторону от сечения.
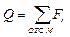
Составим сумму моментов, действующих на отрезанную часть балки, относительно сечения.
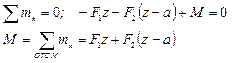
Изгибающий момент равен алгебраической сумме всех моментов, действующих на отсеченную часть бруса, относительно центра тяжести сечения.
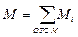
Для того чтобы можно было вести расчет с любого конца балки, необходимо принять правило знаков для внутренних силовых факторов.
Для поперечной силы Q.
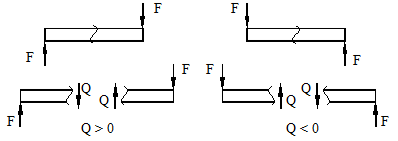
Рисунок 17.
Если внешняя сила вращает отрезанную часть балки по часовой стрелке, то сила является положительной, если внешняя сила вращает отрезанную часть балки против хода часовой стрелки, то сила является отрицательной.
Для изгибающего момент момента М.
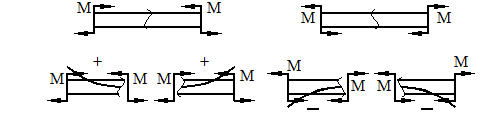
а) б)
Рисунок 18.
Если под действием внешней силы изогнутая ось балки принимает вид вогнутой чаши, такой, что идущий сверху дождь будет наполнять ее водой, то изгибающий момент является положительным (рис. 18а). Если под действием внешней силы изогнутая ось балки принимает вид выпуклой чаши, такой, что идущий сверху дождь не будет наполнять ее водой, то изгибающий момент является отрицательным (рис. 18б).
Между интенсивностью распределенной нагрузки q, поперечной силой Q и изгибающим моментом М, действующим в некотором сечении, существуют следующие дифференциальные зависимости:
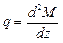 ,
, 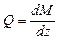 ,
, 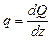 .
.
Указанные дифференциальные зависимости при изгибе позволяют установить некоторые особенности эпюр поперечных сил и изгибающих моментов.
1) На тех участках, где нет распределенной нагрузки, эпюра Q ограничена прямыми, параллельными оси эпюры, а эпюра М, в общем случае, – наклонными прямыми (рис. 19).
2) На тех участках, где к балке приложена равномерно распределенная нагрузка, эпюра Q ограничена наклонными прямыми, а эпюра М – квадратичными параболами (рис. 20). При построении эпюры М на сжатых волокнах, выпуклость параболы обращена в сторону, противоположную действию распределенной нагрузки (рис. 21а, б).
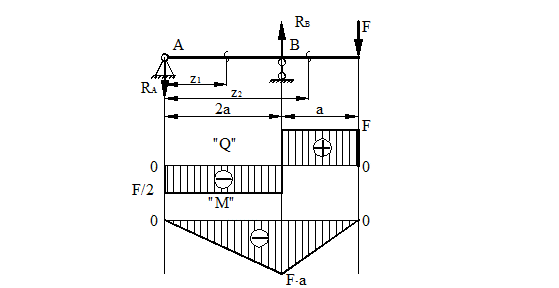
Рисунок 19.
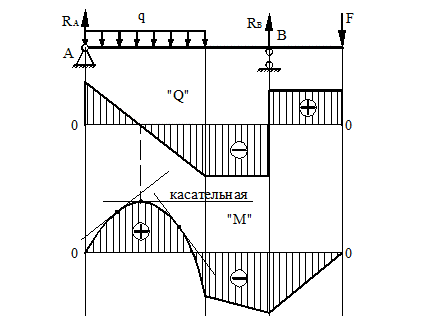
Рисунок 20.
3) В тех сечениях, где Q = 0, касательная к эпюре М параллельна оси эпюры (рис. 20, 21). Изгибающий момент в таких сечениях балки экстремален по величине (Мmax, Mmin).
4) На участках, где Q > 0, M возрастает, то есть слева на право положительные ординаты эпюры M увеличиваются, отрицательные – уменьшаются (рис. 19, 20); на тех участках, где Q < 0, M убывает (рис. 19, 20).
5) В тех сечениях, где к балке приложены сосредоточенные силы:
а) на эпюре Q будут скачки на величину и в направлении приложенных сил (рис. 19, 20).
б) на эпюре M будут переломы (рис. 19, 20), острие перелома направлено против действия силы.
6) В тех, сечениях, где к балке приложены сосредоточенные моменты, на эпюре M будут скачки на величину этих моментов, на эпюре Q никаких изменений не будет (рис. 22).
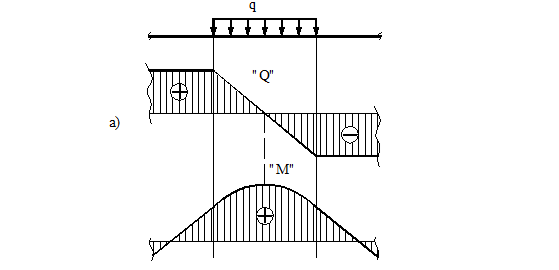
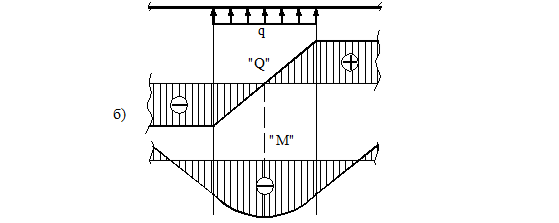
Рисунок 21.
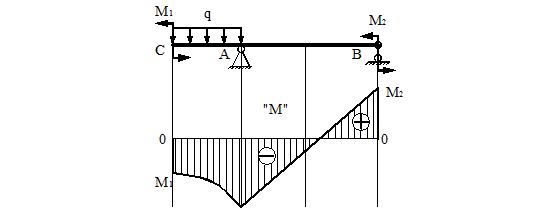
Рисунок 22.
7) Если на конце консоли или в концевой опоре приложен сосредоточенный
момент, то в этом сечении изгибающий момент равен внешнему моменту (сечения C и B на рис. 22).
8) Эпюра Q представляет собой диаграмму производной от эпюры M. Значит, ординаты Q пропорциональны тангенсу угла наклона касательной к эпюре M (рис. 20).
Порядок построения эпюр Q и М:
1) Составляется расчетная схема балки (в виде оси) с изображением действующих на нее нагрузок.
2) Влияние опор на балку заменяется соответствующими реакциями; указываются обозначения реакций и их принятые направления.
3) Составляются уравнения равновесия балки, решением которых определяются значения опорных реакций.
4) Балка разбивается на участки, границами которых являются точки приложения внешних сосредоточенных сил и моментов, а также точки начала и окончания действия или изменения характера распределенных нагрузок.
5) Составляются выражения изгибающих моментов М и поперечных сил Q для каждого участка балки. На расчетной схеме указываются начало и направление отсчета расстояний для каждого участка.
6) По полученным выражениям вычисляются ординаты эпюр для ряда сечений балки в количестве, достаточном для изображения этих эпюр.
7) Определяются сечения, в которых поперечные силы равны нулю и в которых, следовательно, действуют моменты Mmax или Mmin для данного участка балки; вычисляются значения этих моментов.
8) По полученным значениям ординат строятся эпюры.
9) Производится проверка построенных эпюр путем сопоставления их друг с другом.
Эпюры внутренних силовых факторов при изгибе строят для того, чтобы определить опасное сечение. После того, как опасное сечение будет найдено, балку рассчитывают на прочность. В общем случае поперечного изгиба, когда в сечениях стержня действуют изгибающий момент и поперечная сила, в сечении балки возникают нормальные и касательные напряжения. Поэтому, логично рассматривать два условия прочности:
а) по нормальным напряжениям
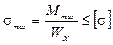
б) по касательным напряжениям
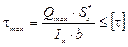
Поскольку основным разрушающим фактором для балок являются нормальные напряжения, то и размеры поперечного сечения балки принятой формы определяют из условия прочности по нормальным напряжениям:
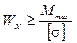
Затем проверяют, удовлетворяет ли выбранное сечение балки условию прочности по касательным напряжениям.
Однако, такой подход к расчету балок еще не характеризует прочность балки. Во многих случаях в сечениях балок имеются точки, в которых одновременно действуют большие нормальные и касательные напряжения. В таких случаях возникает необходимость проверки балки на прочность по главным напряжениям. Наиболее применимы для такой проверки третья и четвертая теории прочности:
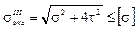 ,
, 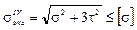 .
.
ПРИМЕР 1
Построить эпюры поперечной силы Q и изгибающего момента М для балки, показанной на рис. 23, если: F1 = 3 кН, F2 = 1,5 кН, М = 5,1 кН∙м, q = =2кН/м, а = 2м, b = 1 м, с = 3м.
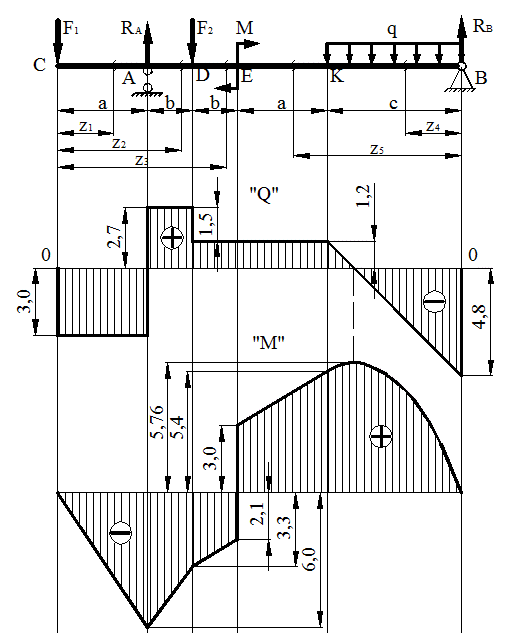
Рисунок 23.
1) Определяем опорные реакции.
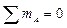 ;
; 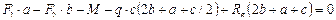 ;
;
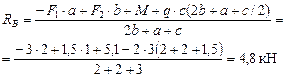
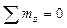 ;
; 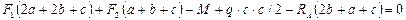 ;
;
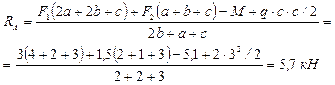
Проверка:
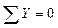 ;
; 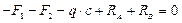 ;
;
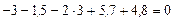 — реакции найдены верно
— реакции найдены верно
2) Разбиваем балку на участки CA, AD, DE, EK, KB.
3) Определяем значения Q и М на каждом участке.
СА 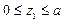
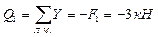
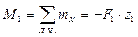
![]() ,
, ![]() ;
; 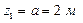 ,
, 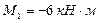 .
.
АD 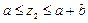
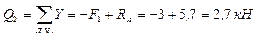
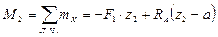
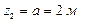 ,
, 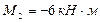 ;
; 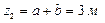 ,
, 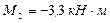 .
.
DE 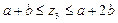
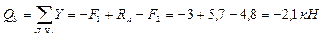
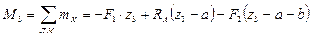
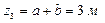 ,
, 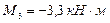 ;
; 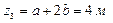 ,
, 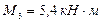 .
.
КВ 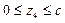
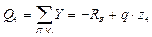
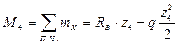
![]() ,
, 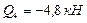 ,
, 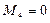 ;
; 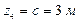 ,
, 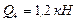 ,
, 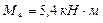 .
.
Найдем максимум изгибающего момента на участке KB.
Приравняем уравнение Q на этом участке к нулю и выразим координату zmax, при которой Q = 0, а момент имеет максимальное значение. Далее подставим zmax в уравнение момента на этом участке и найдем Mmax.
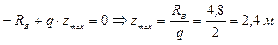
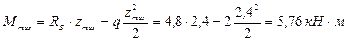
EК 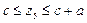
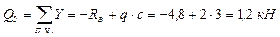
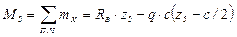
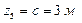 ,
, 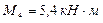 ;
; 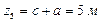 ,
, 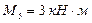 .
.
4) Строим эпюры (рис. 23)
ПРИМЕР 2
Для балки, изображенной на рис. 23 определить размеры круглого, прямоугольного (h/b = 2) и двутаврового сечения. Проверить прочность двутавра по главным напряжениям, если [s] = 150 МПа, [t] = 150 МПа.
1) Определяем из условия прочности необходимый момент сопротивления
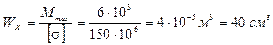
2) Определяем размеры круглого сечения
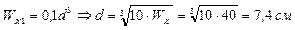
3) Определяем размеры прямоугольного сечения
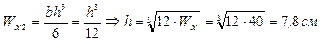
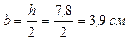
4) Подбираем по сортаменту двутавровую балку № 10 (ГОСТ 8239-89)
WX = 39,7 см3, SX* =23 см3, IX = 198 см4, h = 100 мм, b = 55 мм, d = 4,5 мм, t = 7,2 мм.
Для проверки прочности балки по главным напряжениям, необходимо построить эпюры нормальных и касательных напряжений в опасном сечении. Так как величина главных напряжений зависит и от нормальных и от касательных напряжений, то проверку прочности следует произвести в том сечении балки, где М и Q достаточно велики. На опоре В (рис. 23) поперечная сила Q имеет максимальное значение, однако здесь М = 0. поэтому считаем опасным сечение на опоре А, где изгибающий момент максимален и поперечная сила имеет сравнительно большое значение.
Нормальные напряжения, изменяясь по высоте сечения, подчиняются линейному закону:
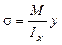 ,
,
где y – координата точки сечения (рис. 24).
при у = 0, s = 0;
при ymax, 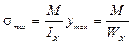
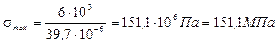
Закон изменения касательных напряжений определяются законом изменением статического момента ![]() площади, который, в свою очередь изменяется по высоте сечения по параболическому закону. Вычислив значение для характерных точек сечения, построим эпюру касательных напряжений. При вычислении значений t воспользуемся обозначениями размеров сечения, принятыми на рис. 24.
площади, который, в свою очередь изменяется по высоте сечения по параболическому закону. Вычислив значение для характерных точек сечения, построим эпюру касательных напряжений. При вычислении значений t воспользуемся обозначениями размеров сечения, принятыми на рис. 24.
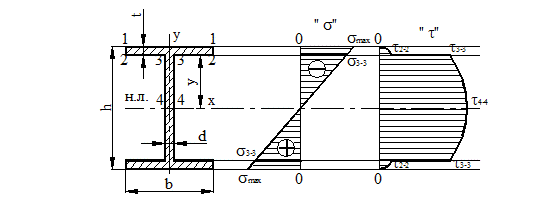
Рисунок 24.
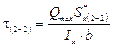 ;
; 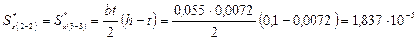 м3
м3
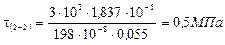
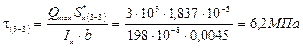
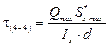
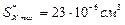
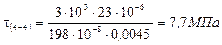
Как видно из эпюр, опасным в сечении является слой 3–3, где нормальные и касательные напряжения имеют значения близкие к максимальным, в то время как в слое 1–1, где 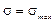 , t = 0, а в слое 4–4, где
, t = 0, а в слое 4–4, где 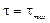 , s = 0.
, s = 0.
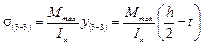
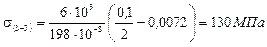
Определяем главные напряжения по третьей теории прочности
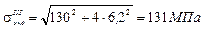
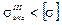 — условие прочности для слоя 3–3 выполняется.
— условие прочности для слоя 3–3 выполняется.
Указания к задаче 7
Совместному действию изгибающего и крутящего моментов подвергаются большинство деталей машин и механизмов, которые кроме скручивания, испытывают изгиб от собственного веса, от веса шкивов, зубчатых колес, от натяжения ремней, от сил зацепления колес и т. д. Расчет на прочность при изгибе с кручением обычно выполняют при расчете валов с учетом изгибающих усилий и при расчете пространственных стержней.
Если внешние силы, действующие на вал, не лежат в одной плоскости, то необходимо разложить их на составляющие: вертикальную и горизонтальную. Далее следует построить эпюру крутящего момента, эпюры изгибающих моментов в вертикальной и горизонтальной плоскостях, а затем эпюру суммарного изгибающего момента.
При совместном действии крутящего и изгибающего моментов необходимо учитывать нормальные напряжения, возникающие от действия изгибающего момента, и касательные напряжения, возникающие от действия крутящего момента. Максимальные эквивалентные напряжения от кручения и изгиба возникающие на поверхности круглого вала определяют по третьей или четвертой теории прочности:
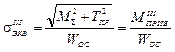 ;
; 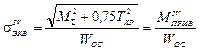 ,
,
где WОС – осевой момент сопротивления сечения.
Условия прочности при изгибе с кручением соответственно по третьей и четвертой теориям прочности записываются:
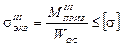 ;
; 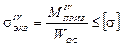 .
.
ПРИМЕР
Подобрать круглое поперечное сечение вала, показанного на рис. 25, если диаметры шкивов d1 = d2 = 200 мм, d3 = 300 мм; углы наклона ремней к горизонту a1 = a2 = 30°, a3 = 45° (рис. 26); мощность на ведущем шкиве 3 N3 = =5кВт; мощность на ведомых шкивах 1 и 2 N1 = N2 = N3 / 2; расстояния а = =0,25 м, b = 0,4м; допускаемые напряжения [s] = 80 МПа. Расчет проводить по третьей теории прочности.
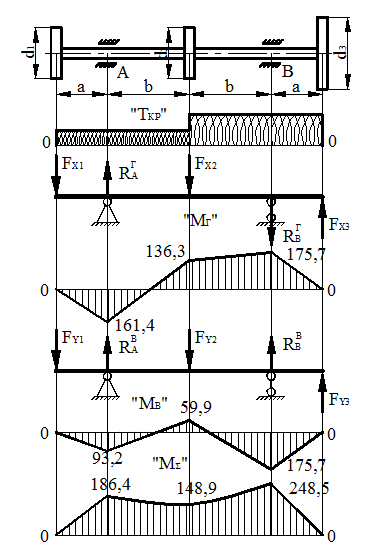
Рисунок 25.
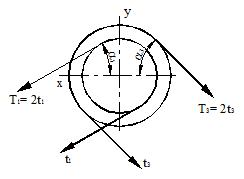
Рисунок 26.
1) Определяем крутящие моменты на валу и строим их эпюру
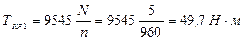
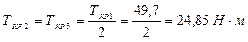
2) Определяем окружные усилия
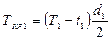 ,
, ![]() ;
;
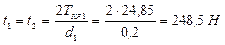
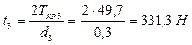
3) Определяем горизонтальные и вертикальные проекции сил, действующих на вал
Для определения проекций сил пользуемся направлениями осей, принятыми на рис. 26.
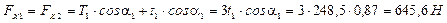
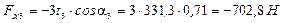
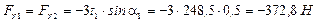
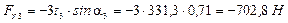
4) Строим эпюру изгибающих моментов в горизонтальной плоскости
Определяем опорные реакции (рис. 25)
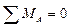 ;
; 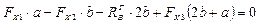
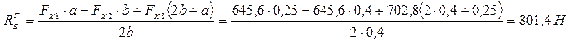
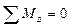 ;
; 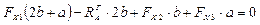
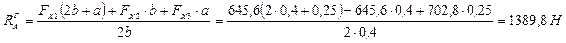
Проверка
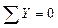 ;
; 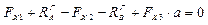
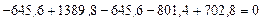 — верно
— верно
Строим эпюру (пример на построение эпюр изгибающих моментов см. в указаниях к задаче № 4).
5) Строим эпюру изгибающих моментов в вертикальной плоскости
Определяем опорные реакции (рис. 25)
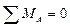 ;
; 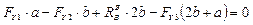
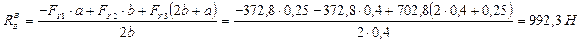
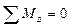 ;
; 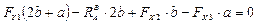
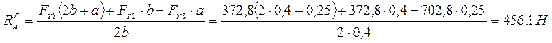
Проверка
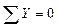 ;
; 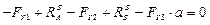
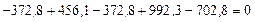 — верно
— верно
Строим эпюру (рис. 25).
6) Строим эпюру суммарного изгибающего момента
Для построения суммарной эпюры изгибающего момента значения ординат в характерных точках берем с эпюр моментов в горизонтальной и вертикальной плоскостях (рис. 25).
В точке А:
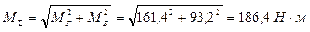
В точке В:
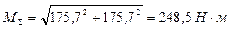
В точке С:
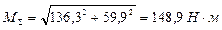
Строим эпюру (рис. 25).
7) Определяем приведенный момент в опасном сечении вала
Опасным сечением вала будет являться сечение в точке В, так как в ней крутящий и суммарный изгибающий моменты имеют наибольшие значения.
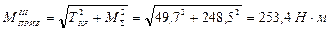
8) Подбираем безопасный диаметр вала
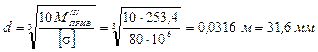
Принимаем d = 35 мм.
Указания к задаче 8
В строительстве, наряду с проблемами прочности и жесткости существует и проблема устойчивости, когда центрально сжатый брус, достаточно большой длины, начинает искривляться под действием внешней силы.
Устойчивым равновесием называется такая форма равновесия сжатого стержня, когда слегка отклоненный от положения равновесия стержень стремится под действием сжимающей силы занять исходное положение.
Критической силой называется такое минимально возможное значение нагрузки, при котором слегка отклоненный стержень теряет свою устойчивость.
При потере устойчивости кроме сжимающей силы, действующей на стержень, возникает дополнительный изгибающий момент. Поэтому в поперечных сечениях стержня происходит значительный рост напряжений, а также значительно возрастают и деформации стержня.
Если в стержне возникают только упругие деформации, то расчет его на устойчивость можно вести по формуле Эйлера:
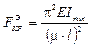 ,
,
где Е – модуль упругости первого рода;
Imin — минимальный момент инерции поперечного сечения стержня;
m — коэффициент приведения длины стержня;
l — длина стержня.
Коэффициент приведения длины стержня m зависит от условий закрепления стержня, его величину можно определить по рис. 27.
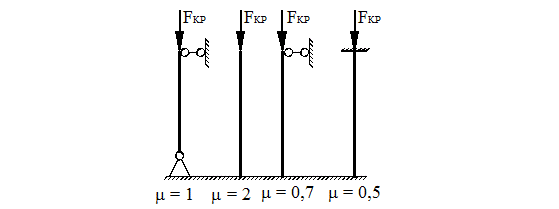
Рисунок 27.
Критические напряжения определяются по формуле:
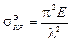 ,
,
где l — гибкость стержня.
Существует другой метод расчета стержней на устойчивость, сочетающий в себе и расчет на прочность. Этот метод известен как расчет по коэффициенту j. При расчете сжатых стержней коэффициент запаса устойчивости принимается большим, чем коэффициент запаса прочности, поэтому можно выразить критическое напряжение в стержне формулой:
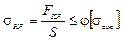
где j — коэффициент снижения допускаемого напряжения на сжатие.
Коэффициент зависит от материала стержня и от его гибкости и определяется по специальным таблицам, его величина всегда меньше единицы. При проектном расчете стержня на устойчивость приходится использовать метод последовательных приближений, задаваясь несколькими значениями коэффициента j.
ПРИМЕР
Подобрать сечение двутаврового стержня, показанного на рис. 28, если длина стержня l = 4 м, сжимающая сила F = 500 кН, допускаемые напряжения на сжатие [s] = 150 МПа.
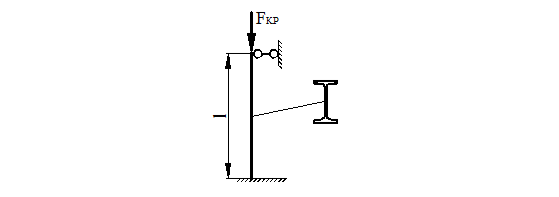
Рисунок 28.
Принимаем первоначальный коэффициент снижения допускаемого напряжения j1 = 0,5. Тогда допускаемое напряжение на устойчивость:
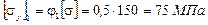 .
.
Определяем необходимую площадь поперечного сечения стержня:
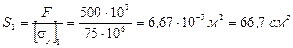
По таблицам сортамента подбираем двутавр № 40: S = 72,6 см2, imin = iy = = 3,03 см.
Находим гибкость стержня. По условию задачи коэффициент m = 0,7.
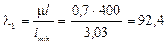
По известной гибкости стержня определяем из таблицы коэффициент j2 (Степин П. А. Сопротивление материалов. М.: Высш. шк., 1988. – 367 с.).
j2 = 0,6684
Определяем допускаемое напряжение на устойчивость:
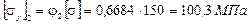 .
.
Определяем рабочее напряжение стержня:
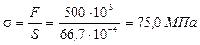
Сравним рабочее и допускаемое напряжение на устойчивость:
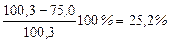 — недонапряжение
— недонапряжение
При расчетах на устойчивость отклонение от допускаемого напряжения не должно превышать 5%, поэтому подобранное сечение слишком велико, и необходимо продолжить подбор сечения, используя метод последовательного приближения.
Определяем из двух величин напряжений среднее напряжение:
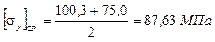
Определяем необходимую площадь поперечного сечения стержня:
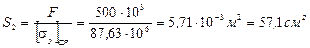
По таблицам сортамента подбираем двутавр № 36: S = 61,9 см2, imin = iy = = 2,89 см.
Находим гибкость стержня:
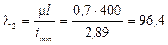
Определяем коэффициент j3:
j3 = 0,6279
Определяем допускаемое напряжение на устойчивость:
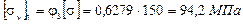 .
.
Определяем рабочее напряжение стержня:
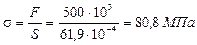
Сравним рабочее и допускаемое напряжение на устойчивость:
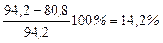 — недонапряжение
— недонапряжение
Подобранное сечение слишком велико, и необходимо продолжить подбор сечения.
Определяем из двух величин напряжений среднее напряжение: