Понятие о деформациях
Главный вектор и главный момент обычно приводятся к центру тяжести сечения С.
По первым буквам вышеизложенной последовательности действий этот метод имеет также название − метод РОЗУ (разрезают, отбрасывают, заменяют, уравновешивают).
Метод РОЗУ позволяет определить не сами внутренние силы, а их интегральные характеристики − главный вектор ![]() и главный момент .
и главный момент .
Разложение этих интегральных характеристик по осям системы координат (рис. 3г), связанной с сечением (оси х и у лежат в плоскости сечения, а ось z − направлена нормально к сечению), даёт шесть силовых составляющих![]()
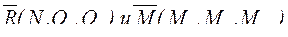 :
:
N − продольная (нормальная) сила, стремящаяся либо оторвать часть 1 от части 2, либо сжать их;
Qx, Qy − поперечные силы, стремящиеся сдвинуть часть 1 относительно 2 по сечению;
Мкр − крутящий момент, пытающийся скрутить часть 1 относительно части 2 по оси z;
Мх, Му − изгибающие моменты, стремящиеся повернуть одно сечения относительно другого вокруг осей x и y соответственно.
Эти составляющие называются внутренними силовыми факторами в сечении рассматриваемого тела. Их можно определить из шести уравнений равновесия отсечённой части:
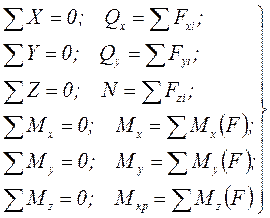 . (1.1)
. (1.1)
Если число неизвестных сил равно числу уравнения равновесия статики, задача называется статически определимой, если же число неизвестных сил больше числа уравнений равновесия – статически неопределимой.
В технике принято при прочностном анализе элементов конструкции в форме бруса изображать графики изменения данных шести силовых факторов прямо на схеме конструкции, т. е. строить так называемые эпюры внутренних силовых факторов, на которых наглядно видны наиболее опасные в прочностном отношении сечения бруса.
1.4. Понятие о деформациях
 В сопротивлении материалов, в отличие от теоретической механики, исследуют поведение конструкций, материал которых способен деформироваться от внешних воздействий. Изменение линейных размеров тела или его частей называется линейной деформацией, а изменение угловых размеров – угловой деформацией. Если на поверхности тела (рис. 4а) вблизи исследуемой точки нанести весьма малый прямоугольник
В сопротивлении материалов, в отличие от теоретической механики, исследуют поведение конструкций, материал которых способен деформироваться от внешних воздействий. Изменение линейных размеров тела или его частей называется линейной деформацией, а изменение угловых размеров – угловой деформацией. Если на поверхности тела (рис. 4а) вблизи исследуемой точки нанести весьма малый прямоугольник 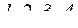 , то в результате деформации этот прямоугольник в общем случае примет форму параллелограмма
, то в результате деформации этот прямоугольник в общем случае примет форму параллелограмма  (рис. 4б).
(рис. 4б).
Абсолютное удлинение Δl характеризует линейную деформацию, а углы α и β – угловую. Отношение абсолютного удлинения Δl к первоначальной длине представляет относительное удлинение:
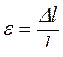 . (1.2)
. (1.2)
Опыты показывают, что деформации после снятия нагрузки могут исчезать полностью или частично.
Деформации, исчезающие полностью после разгрузки тела, называются упругими; такие тела – упругими, а это свойство тел – упругостью.
Деформации, сохраняемые телом после снятия нагрузок, называются пластическими (остаточными); тела – пластичными, а свойство таких тел – пластичностью. В ряде прочностных расчётов их учитывают особо.
Каждый из силовых факторов вызывает определённый вид деформации:
− продольная сила N – деформацию растяжения (сжатия);
− поперечные силы Qx и Qy − деформации сдвига;
− моменты Мх и Мy − деформации изгиба;
− моменты Мкр − деформацию кручения.
1.5. Понятие о напряжениях
 Для оценки уровня внутренних сил в какой-либо точке D (рис. 5) вводится понятие меры интенсивности внутренних сил, которая называется напряжением. Под напряжением понимается отношение внутренней силы к единице площади сечения. В международной системе единиц (SI) напряжение измеряется в паскалях (Па), т. е. в ньютонах на квадратный метр (Н/м2). Удобнее измерять в мегапаскалях (МПа): 1МПа = 106Па.
Для оценки уровня внутренних сил в какой-либо точке D (рис. 5) вводится понятие меры интенсивности внутренних сил, которая называется напряжением. Под напряжением понимается отношение внутренней силы к единице площади сечения. В международной системе единиц (SI) напряжение измеряется в паскалях (Па), т. е. в ньютонах на квадратный метр (Н/м2). Удобнее измерять в мегапаскалях (МПа): 1МПа = 106Па.
Рассмотрим сечение некоторого тела (рис. 5). В окрестности точки D выделим элементарную площадку ∆А, в пределах которой действует внутренняя сила ∆R, разложив которую по осям x, y, z , получим составляющие ΔN, ΔQx, ΔQy.
Тогда средним напряжением в точке D в пределах площадки ∆А будет
![]()
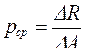 . (1.3)
. (1.3)
Полное напряжение в точке D сечения получим при ∆А→0, т. е.
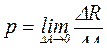 . (1.4)
. (1.4)
Полное напряжение p можно разложить на составляющие:
− напряжение нормальное к плоскости сечения, которое обозначается σ и называется нормальным напряжением:
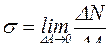 ; (1.5)
; (1.5)
− напряжения, лежащие в плоскости сечения, которые обозначаются τ и называются касательными:
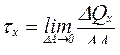 , (1.6)
, (1.6)
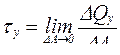 . (1.7)
. (1.7)
Для удобства τ представляют в виде двух составляющих по направлению координатных осей.
Векторы нормального и касательных напряжений совпадают соответственно с векторами нормальной силы ΔN и поперечными силами ΔQx и ΔQy.
1.6. О физической взаимосвязи напряжений и деформаций
Связь между перемещениями и деформациями впервые была сформулирована Робертом Гуком в конце XVII века. В современной интерпретации закон Гука, или гипотеза упругости, устанавливает линейную зависимость между деформациями тела в каждой его точке и напряжениями в той же точке. Коэффициенты пропорциональности в этой зависимости представляют собой физические константы материала, из которого выполнена конструкция, и определяются экспериментально.
В соответствии с законом Гука, указанная прямо пропорциональная зависимость справедлива как при возрастании, так и при убывании нагрузки, что даёт основание говорить об упругих свойствах тел, подчиняющихся этому закону. Закон Гука является приближённым. Для большинства конструкционных материалов (например, стали) он выполняется в определённых пределах уровня напряжений достаточно точно. Для чугуна и ряда строительных материалов существенные отклонения от линейной зависимости проявляются уже при небольших значениях напряжений.
1.7. Общие принципы расчёта элементов конструкций
При работе машин каждый её элемент (деталь) нагружен внешними силами, которые могут привести к недопустимой деформации детали или к её разрушению. Чтобы этого не произошло, необходимо правильно выбрать материал и конструктивные формы детали в зависимости от характера действия сил и условий работы. В результате расчётов при проектировании следует убедиться, удовлетворяет ли конструкция предъявляемым требованиям надёжности.
Методы расчёта выбираются в зависимости от условий работы конструкции и требований, которые к ней предъявляются.
Основным методом расчёта элементов конструкции является расчёт по напряжениям. В основу этого метода положено предположение, что критерием надёжности конструкции является напряжённое состояние в точке. Оно характеризуется совокупностью нормальных и касательных напряжений, действующих по всем площадкам, которые можно провести через рассматриваемую точку.
Из анализа напряжённого состояния конкретной детали выявляются те сечения (точки) её элементов, в которых действуют наибольшие напряжения. Найденные наибольшие напряжения сравниваются с предельным напряжением для данного материала, полученным в лабораторных испытаниях, и делается заключение о прочности конкретного элемента конструкции.


