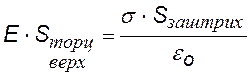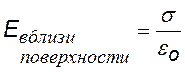Распределение зарядов в проводниках
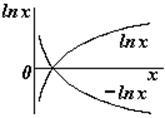
В этом случае принять j = 0 на бесконечности нельзя (см. график
ln x), поэтому выбираем j = 0 в некоторой произвольной точке с координатой ro. Т. е. примем
 j 1 = 0 при r1 = r0,
j 1 = 0 при r1 = r0,
заменим j 2 ® j , r2 ®r получим
j (r)
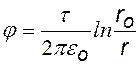
j = 0 при r = r0
4)Бесконечно протяженная плоскость, равномерно заряженная с поверхностной плотностью заряда s (Кл/м2). Выберем на оси координат х две произвольные точки х1 и х2 .). Используем формулу связи Е и j (···), подставим выражение для напряженности поля бесконечной плоскости.
|
|
Чтобы получить выражение для потенциала примем 1)j 1 = 0 при х1 = 0 и 2) j 1 = 0 при х1 = d (d – произвольная точка на оси х) |
|
1) 2) |
|
Следует иметь в виду, что формулы для Е и j в случаях плоскости, нити, цилиндра применимы только на расстояниях от них, существенно меньших размеров этих тел. В действительности при учете краевых эффектов поля становятся более сложными.
Во всех случаях, задавая нулевой уровень потенциала j = 0 в различных точках, мы можем получить сколько угодно формул для потенциала данного поля. Потенциальные кривые (или прямые), т. е. графики j(r)или j(х) при этом будут перемещаться по вертикали параллельно самим себе. В принципе, неважно, где выбрать нулевой уровень потенциала, т. к. во всех задачах имеет значение не сам потенциал, а его изменение
Так как потенциал – скалярная величина, а напряженность – вектор, то значительно проще найти сначала зависимость j(r) или j(х), затем дифференцируя, получить формулу для Е(r)или Е (х).
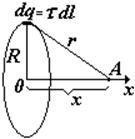
В качестве примера найдем потенциал поля на оси тонкого кольца, равномерно заряженного с линейной плотностью t, а затем Е (х).Для этого выделим в кольце бесконечно малый элемент dl с зарядом dq = t×dl (см. рис.) В некоторой точке A потенциал складывается из потенциалов, создаваемых всеми элементами кольца.
|
|
потенциал поля элементарного заряда dq (j¥ = 0) |
|
|
|
«суммируя» (интегрируя) потенциалы от всех элементов кольца, получим формулу для j (х). |
|
|
|
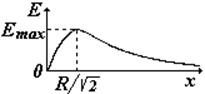
Дифференцируя по х, найдем напряженность Е(х) |
|
|
|
|
|
Распределение зарядов в проводниках.
Металлические проводники в целом являются нейтральными: в них поровну отрицательных и положительных зарядов. Положительно заряженные – это ионы в узлах кристаллической решетки, отрицательные – электроны, свободно перемещающиеся по проводнику. Когда проводнику сообщают избыточное количество электронов, он заряжается отрицательно, если же у проводника «отбирают» какое-то количество электронов, он заряжается положительно.
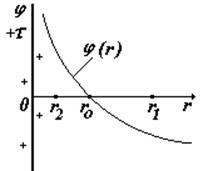
 Избыточный заряд распределяется только по внешней поверхности проводника. Если проводник полый, то на его внутренних поверхностях нет зарядов. Это используют для полной передачи заряда от одного проводника другому (см. рис.).
Избыточный заряд распределяется только по внешней поверхности проводника. Если проводник полый, то на его внутренних поверхностях нет зарядов. Это используют для полной передачи заряда от одного проводника другому (см. рис.).
Отсутствие поля внутри полости в проводнике позволяет создать электростатическую защиту. Проводник или достаточно густая металлическая сетка, окружающие со всех сторон некоторую область, экранируют ее от электрических полей, созданных внешними зарядами.
В электростатике рассматривается стационарное, неизменное распределение зарядов. Условием стационарности является равенство нулю напряженности поля внутри проводника: Е = 0. Если бы напряженность не была равна нулю, это создало бы электрические силы, вызывающие направленное перемещение электронов, т. е. электрический ток.
Избыточные заряды, сообщаемые проводнику, распределяется равномерно только по поверхности металлических сферы или шара. Во всех остальных случаях заряды распределяются неравномерно: чем больше кривизна поверхности, тем больше поверхностная плотность зарядов на поверхности проводника. Докажем это. Возьмем два шара радиусами R1 и R2, заряженные зарядами q1 и q2 , соответственно. Соединим их проволочкой. Заряды будут перемещаться с одного шара на другой до тех пор, пока потенциал всей системы не станет одинаковым. Влиянием проволочки будем пренебрегать.
|
|
потенциалы заряженных сфер до их соединения |
|
|
|
после соединения шаров – общий потенциал равен j, полученное соотношение можно записать как: |
|
|
s×R = const s ~ 1/R |
Заряд распределяется по поверхности так, что его поверхностная плотность s обратно пропорциональна радиусу кривизны поверхности |
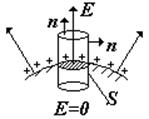
Найдем напряженность поля заряженного проводника вблизи его поверхности, используя теорему Гаусса. Весь проводник представляет собой одну эквипотенциальную поверхность. Силовые линии перпендикулярны эквипотенциальным поверхностям. Выберем в качестве гауссовой поверхности S цилиндр очень малого размера, образующие которого перпендикулярны поверхности проводника (см. рис.). В пределах цилиндра поверхностную плотность заряда s будем считать постоянной.
|
|
Разобьем интеграл потока на три: по боковой, по нижней торцевой и по верхней торцевой поверхностям. Первый интеграл = 0, т. к. cosa = 0, второй интеграл = 0, т. к. Е = 0. Получим: |
|
|
|
Т. к. заштрихованная площадь равна верхней торцевой площади, то напряженность поля непосредственно у самой поверхности оказывается пропорциональной поверхностной плотности заряда. |
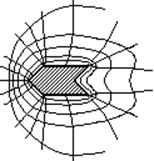 Таким образом, чем более искривлена поверхность заряженного проводника, тем больше скапливается на ней зарядов и тем больше оказывается напряженность поля в этом месте. На рис. показаны силовые линии и эквипотенциальные поверхности поля заряженного тела. Наибольшая напряженность получается у острых выступов поверхности. Это приводит к так называемому «стеканию зарядов». В действительности из-за высокой напряженности вблизи острия возникают сложные явления: могут ионизироваться молекулы воздуха, дипольные молекулы втягиваются в область более сильного поля, в результате скорость потока частиц от острия оказывается большей, и образуется «электрический ветер». Этот ветер может привести во вращение легкое колесо, находящееся вблизи острия. Воздух становится проводящей средой, возникает разряд, вблизи острых концов часто наблюдается свечение. Поэтому всем деталям в электроустановках, находящихся под высоким напряжением, придают закругленную форму и делают их поверхности гладкими.
Таким образом, чем более искривлена поверхность заряженного проводника, тем больше скапливается на ней зарядов и тем больше оказывается напряженность поля в этом месте. На рис. показаны силовые линии и эквипотенциальные поверхности поля заряженного тела. Наибольшая напряженность получается у острых выступов поверхности. Это приводит к так называемому «стеканию зарядов». В действительности из-за высокой напряженности вблизи острия возникают сложные явления: могут ионизироваться молекулы воздуха, дипольные молекулы втягиваются в область более сильного поля, в результате скорость потока частиц от острия оказывается большей, и образуется «электрический ветер». Этот ветер может привести во вращение легкое колесо, находящееся вблизи острия. Воздух становится проводящей средой, возникает разряд, вблизи острых концов часто наблюдается свечение. Поэтому всем деталям в электроустановках, находящихся под высоким напряжением, придают закругленную форму и делают их поверхности гладкими.
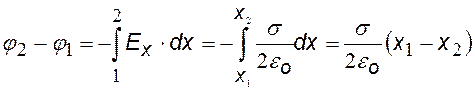
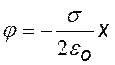 j = 0 при х = 0
j = 0 при х = 0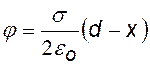 j = 0 при х = d
j = 0 при х = d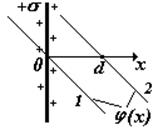
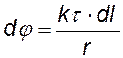
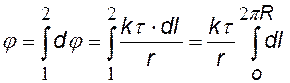
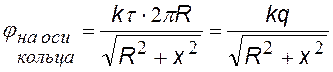
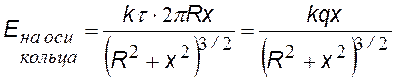
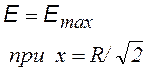
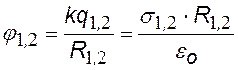
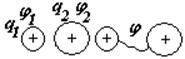
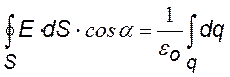 Þ
Þ