Скорость и ускорение мсс
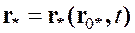 .
.
Но это уравнения движения одной выбранной материальной точки, где вместо ее номера (как было в теоретической механике) введены ее координаты в начальный момент времени. Характерно, что координаты любой материальной частицы, которые они имели в начальный момент времени, в процессе движения меняться не будут. И если 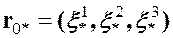 пробегает все точки начального состояния, то (1.3) позволит определить координаты всех этих же материальных точек (которые в силу следствия из гипотезы непрерывности остаются материальными точками) в любой момент времени. По этой причине координаты материальных точек в начальный момент времени называются материальными координатами или лагранжевыми координатами. Координаты же тех точек пространства, в которых находятся материальные частицы в момент времени
пробегает все точки начального состояния, то (1.3) позволит определить координаты всех этих же материальных точек (которые в силу следствия из гипотезы непрерывности остаются материальными точками) в любой момент времени. По этой причине координаты материальных точек в начальный момент времени называются материальными координатами или лагранжевыми координатами. Координаты же тех точек пространства, в которых находятся материальные частицы в момент времени ![]() , называются пространственными координатами или эйлеровыми координатами. С другой стороны, соотношения (1.4) можно рассматривать как отображение, позволяющее найти начальные (материальные) координаты частиц, находящихся в данный момент времени
, называются пространственными координатами или эйлеровыми координатами. С другой стороны, соотношения (1.4) можно рассматривать как отображение, позволяющее найти начальные (материальные) координаты частиц, находящихся в данный момент времени ![]() в точках пространства, определяемых радиус-вектором
в точках пространства, определяемых радиус-вектором 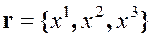 . Интересно отметить, что для описания различных процессов в СС мы можем выбирать или материальные, или пространственные координаты. Если выбраны материальные координаты, то (1.3) позволяет определить пространственные, а если выбраны пространственные, то (1.4) позволяют определять материальные.
. Интересно отметить, что для описания различных процессов в СС мы можем выбирать или материальные, или пространственные координаты. Если выбраны материальные координаты, то (1.3) позволяет определить пространственные, а если выбраны пространственные, то (1.4) позволяют определять материальные.
Определение. Если в качестве независимых выбраны материальные координаты, а определяющие и искомые физические поля являются функциями этих координат и времени, то говорят, что используется лагранжево описание движения СС. Если в качестве независимых выбраны пространственные координаты, а определяющие и искомые физические поля являются функциями этих координат и времени, то говорят, что используется эйлерово описание движения СС.
Пример. В качестве примера рассмотрим скалярное поле температур, которое имеет текущая река. Представим себе ситуацию, когда к каждой материальной частице воды прикреплен градусник, перемещающийся так же как и частица. Взглянув в некоторый момент времени на эти градусники, мы увидим поле температур в данный момент. Теперь рассмотрим ситуацию, кода все градусники прикреплены к точкам пространства. Каждый градусник показывает температуру той частицы воды, которая омывает его в данный момент. Взглянув на эти градусники в тот же момент времени, мы увидим то же поле температур. И хотя в первом случае градусники перемещались, а во втором находились в покое, поле температур в один и тот же момент времени они показывали одинаковое. В первом случае использовалось лагранжево описание, а во втором эйлерово.
1.4 СКОРОСТЬ И УСКОРЕНИЕ
Скорость частицы. Определим скорость частицы как быстроту изменения ее радиус-вектора во времени. Т. к. понятие скорости относится к частице, то для ее определения требуется описание Лагранжа. Для каждой частицы согласно (1.3) ее радиус-вектор ![]() должен быть постоянным во время движения, поэтому скорость выбранной частицы определяется частной производной, т. е. по определению
должен быть постоянным во время движения, поэтому скорость выбранной частицы определяется частной производной, т. е. по определению
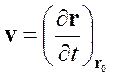 (1.5)
(1.5)
есть скорость частицы ![]() , и соответственно из (1.3)
, и соответственно из (1.3)
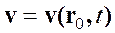 (1.6)
(1.6)
Пространственное описание получим, исключив ![]() из (1.6) при помощи обратного преобразования (1.4).
из (1.6) при помощи обратного преобразования (1.4).
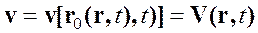 (1.7)
(1.7)
В соответствии с этим соотношением скорость в данной точке оказывается функцией времени, и, следовательно, эйлерово поле скоростей движущегося континуума представляется в виде (1.7).
Понятие субстанциональной производной. Часто необходимо знать, как меняются со временем физические поля, если они определяются самими частицами.
Например, требуется оценить изменение поля температур жидкости в фиксированных точках пространства, когда вполне очевидно, что температуру определяют частицы жидкости, омывающие рассматриваемые точки пространства.
Пусть рассматривается тензорное поле, соответствующее некоторое физической величине. Примем условие: при описании Лагранжа тензорное поле обозначается малыми буквами ![]() , а при описании Эйлера — большими
, а при описании Эйлера — большими ![]() , хотя поле физической величины одно и то же. Например, скалярное поле давлений в жидкой среде обозначим
, хотя поле физической величины одно и то же. Например, скалярное поле давлений в жидкой среде обозначим ![]() — при лагранжевом описании, и
— при лагранжевом описании, и ![]() — при эйлеровом описании. Очевидно, что при разных описаниях имеем две функции, каждая из которых зависит от соответствующих координат и времени
— при эйлеровом описании. Очевидно, что при разных описаниях имеем две функции, каждая из которых зависит от соответствующих координат и времени
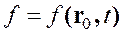 (1.8)
(1.8)
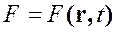 (1.9)
(1.9)
Проанализируем изменение физической величины во времени в материальном и пространственном описании, для чего проводим операцию дифференцирования по времени
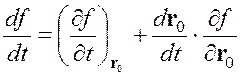 (1.10)
(1.10)
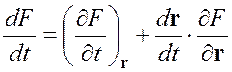 (1.11)
(1.11)
Но в соответствии с (1.3) и (1.5)
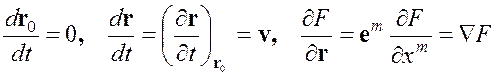 ,
,
что позволяет записать предыдущие равенства в виде:
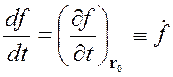 (1.12)
(1.12)
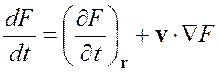 (1.13)
(1.13)
Из (1.12) следует, что в материальном описании полная производная по времени полевой величины совпадает с субстанциональной производной по времени. А из (1.13) вытекает, что в пространственном описании полное изменение физической величины в единицу времени равно сумме локального изменения ![]() в точке
в точке ![]() и конвективного изменения
и конвективного изменения ![]() , связанного с перемещением элемента массы, находящегося в данной точке пространства со скоростью центра массы
, связанного с перемещением элемента массы, находящегося в данной точке пространства со скоростью центра массы ![]() .
.
Ускорение частицы. Определим ускорение частицы как быстроту изменения ее скорости во времени. Для нахождения ускорения из определения следует, что надо выбирать материальное описание, тогда
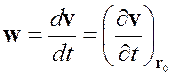 (1.14)
(1.14)
Если же полевая характеристика скорости выражена в пространственных переменных, то полное изменение скорости по (1.13) находится в виде
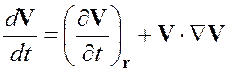 (1.15)
(1.15)
причем согласно принятому условию здесь поле скоростей обозначено большой буквой.
1.5 МЕРЫ ФИЗИЧЕСКИХ ВЕЛИЧИН
О мерах физических величин. Для описания эволюции той или иной системы необходимо использовать физические законы. Такие законы устанавливаются экспериментально на протяжении многочисленных наблюдений, заключений и выводов о ее поведении. Чтобы эти законы выразить в виде математических формул, необходимо учитывать балансные соотношения между физическими характеристиками, принимаемыми для описания эволюции, различных категорий или различной природы.


