Тензор деформации грина
Совокупное расположение материальных частиц друг относительно друга называется конфигурацией. Конфигурацию в начальный момент назовем начальной или отсчетной, а конфигурацию в текущий момент времени будем называть текущей или актуальной.
В процессе движения СС изменяет свою конфигурацию (конфигурация не менялась бы, если бы тело двигалось как абсолютно твердое). Изменение конфигурации связано деформацией в физическом смысле. Для того чтобы выразить деформацию математически, необходимо ввести какую-либо меру деформации. Для этого рассмотрим две конфигурации СС, и оценим изменение расстояния между двумя произвольными бесконечно близкими точками. Пусть в отсчетной конфигурации эти точки суть ![]() и
и ![]() см. рис. 2. Все материальные точки, которые располагались на бесконечно малом отрезке
см. рис. 2. Все материальные точки, которые располагались на бесконечно малом отрезке ![]() в отсчетной конфигурации, будут находиться на бесконечно малой дуге
в отсчетной конфигурации, будут находиться на бесконечно малой дуге 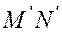 (по следствию из гипотезы непрерывности). Длина этой дуги с точность до величин более высокого порядка малости, равна длине бесконечно малого отрезка
(по следствию из гипотезы непрерывности). Длина этой дуги с точность до величин более высокого порядка малости, равна длине бесконечно малого отрезка 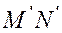 . Для оценки изменения расстояний между точками до деформации и после, рассмотрим разность квадратов расстояний между этими точками. Векторы
. Для оценки изменения расстояний между точками до деформации и после, рассмотрим разность квадратов расстояний между этими точками. Векторы 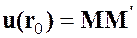 и
и 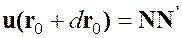 называются векторами перемещений точек
называются векторами перемещений точек ![]() и
и ![]() соответственно. Будем считать, что поле векторов перемещений всех точек является функцией лагранжевых координат. Тогда
соответственно. Будем считать, что поле векторов перемещений всех точек является функцией лагранжевых координат. Тогда
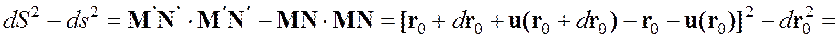
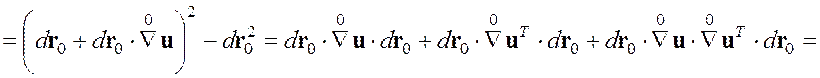
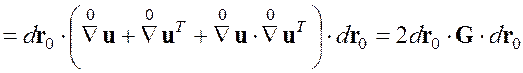 ,
,
где введен тензор
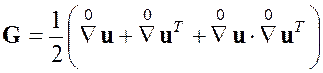 , (2.1)
, (2.1)
называемый тензором деформации Грина.
С другой стороны, мы могли считать поле векторов перемещений функцией эйлеровых координат. Тогда проделывая аналогичные действия, можно получить
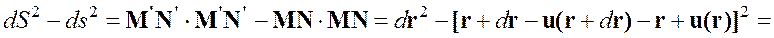
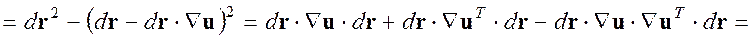
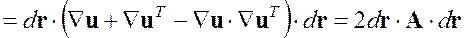 ,
,
где введен тензор
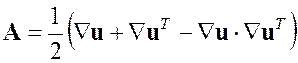 , (2.2)
, (2.2)
называемый тензором деформации Альманси.
2.2 ГЕОМЕТРИЧЕСКИ ЛИНЕЙНАЯ МЕХАНИКА
Достаточно широкий класс задач описывается соотношениями геометрически линейной механики, основанной на предположении о малости перемещений по сравнению с линейными размерами деформируемого тела и поворотов по сравнению с единицей (ограничения не распространяются на смещения как абсолютно твердого тела). Пусть ![]() — характерный линейный размер тела, тогда указанные предположения записываются в виде
— характерный линейный размер тела, тогда указанные предположения записываются в виде
1. 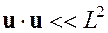 ;
;
2. 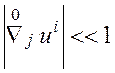 .
.
Т. к. 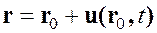 и
и 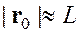 , а
, а 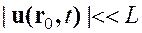 , то
, то
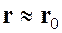 и
и 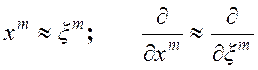 ,
,
но тогда
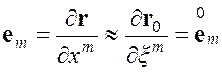 .
.
Таким образом, в геометрически линейной механике пренебрегают различием между пространственными и материальными координатами. Кроме того,
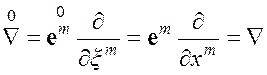
Второе условие позволяет оценить 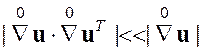 , после чего тензор Грина можно представить в виде
, после чего тензор Грина можно представить в виде
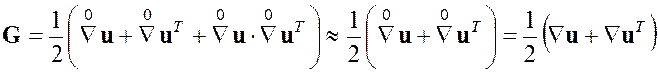 .
.
Совершенно аналогично преобразуется и тензор деформации Альманси
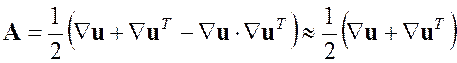 .
.
В этом случае тензор Грина и тензор Альманси совпадают, его обозначают
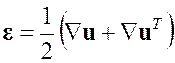 (2.3)
(2.3)
и называют тензором деформации Коши.
2.3 ГЕОМЕТРИЧЕСКИЙ СМЫСЛ КОМПОНЕНТ ДЕФОРМАЦИИ
Наглядная геометрическая интерпретация нелинейных компонент тензоров деформации Грина и Альманси невозможна. Однако можно установить связь с измеряемыми относительными деформациями. Предположим, что рассматривается тензор деформации Грина. Пусть задан малый недеформированный элемент ![]() , который в процессе деформации переходит в элемент
, который в процессе деформации переходит в элемент 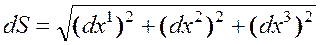 как показано на рис.
как показано на рис.
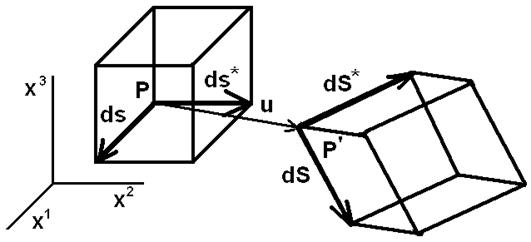
Относительная деформация определяется как относительное изменение длины
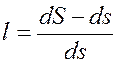 ,
,
откуда длина элемента в текущей конфигурации
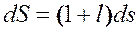 .
.
Но согласно лагранжевому описанию, относительная деформация определяется по отношению к первоначальной длине, следовательно
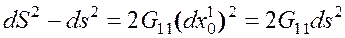 .
.
Из двух последних равенств получаем
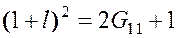 ,
,
из которого очевидно, что относительные удлинения бесконечно малого элемента, совпадающего по направлению в отсчетной конфигурации с направлением первой координатной оси, связаны с первым компонентом тензора деформации Грина. Аналогичные правила имеют место и для других направлений.
Пусть теперь рассматриваются два недеформированных ортогональных линейных элемента в отсчетной конфигурации ![]() и
и ![]() , которые переходят соответственно в элементы
, которые переходят соответственно в элементы ![]() и
и ![]() .Скалярное произведение линейных элементов после деформации дает
.Скалярное произведение линейных элементов после деформации дает
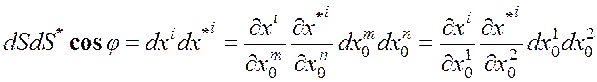 .
.


