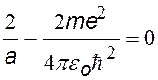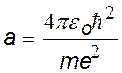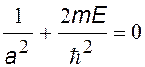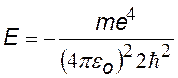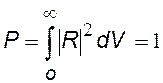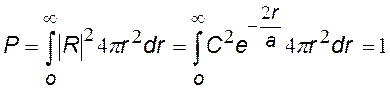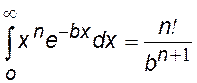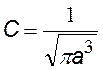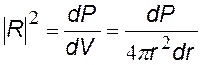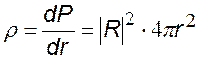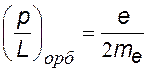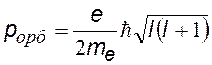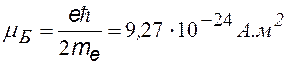Уравнение шрёдингера для электрона в атоме водорода
R, Q и F, т. е. разделим переменные. Нижние индексы показывают, какие квантовые числа (см. дальше) появляются в решениях для этих функций.
Мы будем рассматривать только радиальную часть оператора Лапласа, иначе говоря, случай, когда атом водорода находится в основном состоянии. Функция R называется радиальной частью пси-функции.
|
|
Уравнение Шрёдингера для электрона в атоме водорода в основном состоянии |
||
|
|
Решение уравнения |
|
потенциальная энергия электрона в атоме водорода (U¥ = 0) |
При решении нам нужно определить: полную энергию Е электрона и неизвестные величины С и а. Найдем производные R¢ и R ² , подставим их и R в уравнение Шрёдингера.
|
|
|
|
После сокращений получим уравнение (·), в котором 2-й и 4-й члены содержат r, а два других — нет. Т. к. это уравнение должно выполняться при любых r, в том числе при r = 0, то из (·) мы получим два уравнения, из которых найдем а и Е.
|
|
|
Мы получили выражение, которое точно совпадает с 1-ым боровским радиусом |
|
|
|
Это выражение совпадает с выражением для энергии электрона на первой боровской орбите. |
Коэффициент С найдем из условия нормировки.
|
|
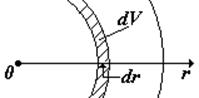
Элементарный объем dV в сферически симметричном случае – это сферический слой толщиной dr, объем слоя |
|
|
|
В математике такой интеграл известен, x=r, n=2, b=2/a |
|
В результате получим:
|
|
Введем понятие радиальной плотности вероятности. Плотность вероятности в нашем случае – это çR ç2 – по определению равна
|
|
где dP вероятность обнаружить электрон в элементарном объеме dV. |
|
|
|
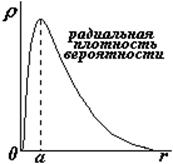
r называется радиальная плотность вероятности — по смыслу – это вероятность обнаружить электрон в сферическом слое единичной толщины |
Из рисунка видно, что максимальная вероятность обнаружить электрон при наименьшей его энергии совпадает с 1-ым боровским радиусом а. Энергия электрона в атоме водорода квантуется, выражение для нее получается такое же, как в теории Бора, но из приведенного выше решения это не следует, т. к. мы рассматривали только основное состояние.
КВАНТОВЫЕ ЧИСЛА
При решении уравнения Шрёдингера автоматически (т. е. без каких либо искусственных предположений) появляются целые числа, которые называются квантовыми числами. Таких чисел три: n, l и m. Впоследствии из релятивистского уравнения Дирака следовало и четвертое квантовое число ms. Каждое из квантовых чисел входит в выражение какой-либо физической величины и свидетельствует о том, что данная величина квантуется, т. е. может принимать дискретные значения. Состояние электрона в квантовой системе полностью
описывается с помощью 4-х квантовых чисел: n, l, m, ms.
|
1) n = 1, 2, 3, … , ¥ главное квантовое число |
входит в выражение для энергии электрона [xvi] Для основного состояния атома Н (n = 1) – см. ранее. |
|
2) l = 0, 1, 2, … , (n — 1) — орбитальное квантовое число, Входит в выражения для орбитальных механического Lорб и магнитного pорб моментов электрона в атоме. Показывает, что орбитальные моменты квантуются, т. е. могут принимать только дискретные значения. |
|
|
|
Как векторы они направлены противоположно |
|
механический орбитальный момент (момент импульса) |
|
|
|
|
|
магнитный орбитальный момент me – масса электрона |
|
|
магнетон Бора; (магнитные моменты принято выражать в магнетонах Бора) |
|
3) m = —l, … , —1, 0, +1, … , +l — магнитное квантовое число Входит в выражение для проекций орбитальных моментов на направление Z внешнего поля (например, магнитного). Показывает, что плоскость, в которой движется электрон во внешнем поле ориентируется только определенным образом, так чтобы проекция момента была кратна Рефераты по физике сдают здесь
Другие статьиПохожая информацияУзнать стоимость за 15 минут
Распродажа дипломных
Подпишись на наш паблик в ВК
Нужна работа?
|
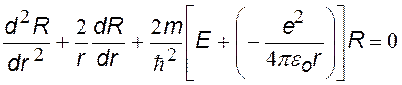
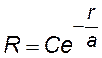
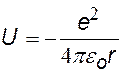
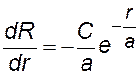
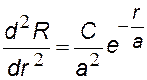
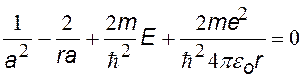 (·)
(·)