Введение в механику сплошной среды — примеры
Пример. Пусть изучается движение некоторого тела. Характер движения может измениться, если на него начнут воздействовать окружающие тела либо непосредственными толчками, либо воздействием на расстоянии полем, либо как-то иначе. Таким образом, необходимо рассмотреть баланс, с одной стороны которого есть движение тела, а с другой воздействие.
Чтобы внести в балансные соотношения, выраженные математическими формулами, физические характеристики различной физической природы необходимо их «оценить» или «измерить» не только качественно, но и количественно. Именно такие меры и входят в балансные соотношения.
Замечание. При определении пространства и времени были введены два физических параметра ![]() и
и ![]() , связанных с расстоянием и временем. Они входят в балансные соотношения, но не относятся к мерам физических величин, а только выражают факт двух форм существования материи (пространство и время).
, связанных с расстоянием и временем. Они входят в балансные соотношения, но не относятся к мерам физических величин, а только выражают факт двух форм существования материи (пространство и время).
Приведем следующие меры, которые используются в МСС.
Масса. Мерой количества вещества является масса. Пусть в объеме ![]() сплошной среды содержится масса
сплошной среды содержится масса ![]() . Т. к. масса распределена по этому объему, то можно ввести функцию плотности массы
. Т. к. масса распределена по этому объему, то можно ввести функцию плотности массы ![]() , согласно следующему равенству
, согласно следующему равенству
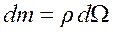 .
.
Масса является экстенсивным параметром, поэтому она аддитивна. Для произвольного объема ![]() его масса
его масса ![]() находится следующим образом
находится следующим образом
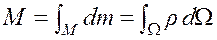 . (1.16)
. (1.16)
Сила. Под силой, действующей на материальную точку, будем понимать некоторую меру воздействия на нее со стороны других материальных объектов, которая, оказывает побуждающее к движению действие. Силы могут иметь различную природу, например, появляться при контакте с другими телами, или возникать в результате действия электрических, магнитных и гравитационных полей, но самым общим, их объединяющим признаком, является их побуждающее к движению действие. Поэтому одинаковые движения одной и той же точки, вызванные разными по физической природе воздействиями можно охарактеризовать одной и той же мерой их воздействия, т. е. силой, и при этом полностью отвлечься от самой природы этого воздействия. Если силы распределены в объеме ![]() , то можно ввести объемную плотность силы
, то можно ввести объемную плотность силы ![]() и определить результирующую силу
и определить результирующую силу ![]() как
как
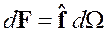 .
.
Можно также ввести массовую плотность силы ![]() , как величину силы, действующую на единицу массы, тогда
, как величину силы, действующую на единицу массы, тогда
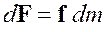 .
.
Из равенства сил, стоящих в левой части двух предыдущих формул, вытекает
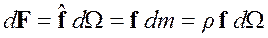 или
или 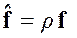 .
.
Сила также является аддитивной величиной, поэтому результирующая сила ![]() объема
объема ![]() находится следующим образом
находится следующим образом
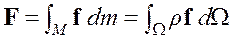 . (1.17)
. (1.17)
Аналогично можно рассмотреть поверхностную плотность силы ![]() , и определить результирующую силу
, и определить результирующую силу ![]() , действующую на поверхности
, действующую на поверхности ![]() как
как
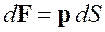 .
.
Результирующая сила на поверхности ![]() находится по формуле
находится по формуле
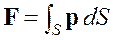 . (1.18)
. (1.18)
Момент силы. Момент силы относительно некоторого центра, например, относительно начала координат, определяется по самой силе следующим образом
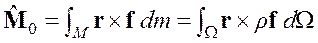 . (1.19)
. (1.19)
Количество движения. Определив материальную точку, и, дав определение ее движения, можно определить и меру поступательного движения материальной точки как произведение ее массы на ее скорость. В МСС при использовании материальных координат можно определить количество движения частицы с массой ![]() и скоростью
и скоростью ![]() как
как 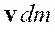 , т. е.
, т. е.
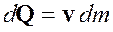
Мера количества движения также является экстенсивным параметром, поэтому для СС, заключенной в произвольном объеме ![]() , в котором содержатся одни и те же частицы, количество движения определяется следующим образом
, в котором содержатся одни и те же частицы, количество движения определяется следующим образом
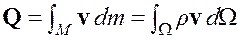 . (1.20)
. (1.20)
Момент количества движения. «Внешний» момент количества движения относительно начала системы координат, заданной эйлеровыми координатами 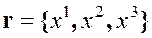 , определяется по количеству движения поступательного движения следующим образом
, определяется по количеству движения поступательного движения следующим образом
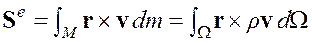 . (1.21)
. (1.21)
«Внутренний» момент количества движения относится к внутреннему вращению выбранного элемента массы континуума определяется следующим образом
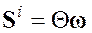 , (1.22)
, (1.22)
где ![]() — макроскопическое среднее внутренних моментов инерции,
— макроскопическое среднее внутренних моментов инерции, ![]() — угловая скорость внутреннего вращения. Чтобы описать превращения «внешнего» и «внутреннего» моментов количества движения друг в друга с помощью неравновесной термодинамики, следует ввести аксиальный вектор
— угловая скорость внутреннего вращения. Чтобы описать превращения «внешнего» и «внутреннего» моментов количества движения друг в друга с помощью неравновесной термодинамики, следует ввести аксиальный вектор
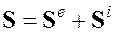 (1.23)
(1.23)
2 ОСНОВНЫЕ ТЕНЗОРНЫЕ ВЕЛИЧИНЫ
2.1 ТЕНЗОР ДЕФОРМАЦИЙ
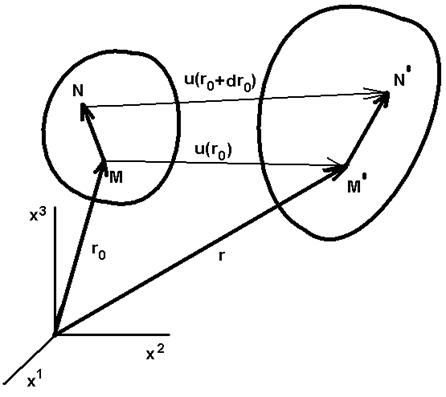 В деформируемых твердых телах важна такая характеристика, как деформация дела. Деформация появляется тогда, когда материальные частицы изменяют свое положение друг относительно друга. Поэтому введем следующие определения.
В деформируемых твердых телах важна такая характеристика, как деформация дела. Деформация появляется тогда, когда материальные частицы изменяют свое положение друг относительно друга. Поэтому введем следующие определения.


