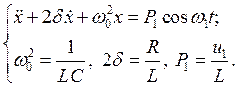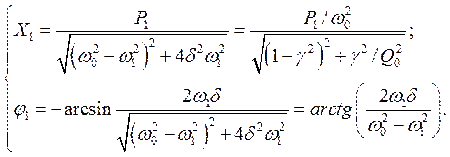Вынужденные колебания в системе с одной степенью свободы
Составим уравнение движения в этом контуре
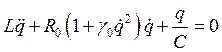 .
.
Вводя, как обычно, новые переменные x = q/q0 и t = w0t, где 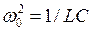 , получим уравнение
, получим уравнение
![]() , где
, где ![]() ,
, 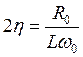 .
.
При малом затухании, когда 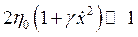 для приближённого решения задачи можно применить метод ММА. Тогда исходное уравнение удобно записать в виде
для приближённого решения задачи можно применить метод ММА. Тогда исходное уравнение удобно записать в виде
![]() .
.
Используя (3.15) и (3.16) для X и q имеем укороченные уравнения
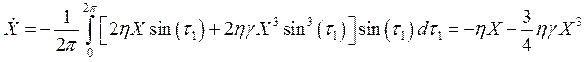 ;
;
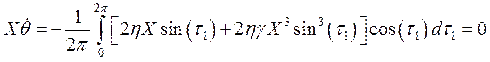 .
.
Первое из этих уравнений домножим на 2X и сделаем замену y = X2, тогда
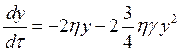 .
.
После преобразований получаем:
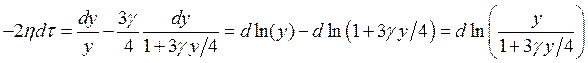 .
.
Это уравнение легко интегрируется:
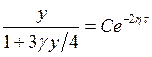 , или
, или 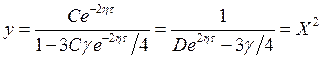 ,
,
где D — постоянная, определяемая из начальных условий. Если в начальный момент при t = 0 X(0) = X0, то
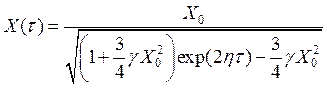 .
.
Полученное соотношение для X выражает закон уменьшения амплитуды колебаний в исследуемом нелинейном контуре, начиная от исходного значения X0.
Отметим также, что, как следует из проведённого рассмотрения, величиной, определяющей ход процесса, является амплитуда колебаний, а фаза колебаний не играет никакой роли. Это обстоятельство вполне понятно, так как характер движения задаётся исходным запасом колебательной энергии, сообщённой контуру вначале процесса, а фаза колебаний никак не определяет ход колебания — соответствующим выбором произвольного для автономной системы начала отсчёта времени фазу можно сделать любой.
Тема 4. Вынужденные колебания в системе с одной степенью свободы Вопрос 9
Как мы уже говорили, колебания в системе под действием внешней периодической силы называются вынужденными. Свойства этих колебаний зависят не только от параметров системы, но и от частоты и амплитуды внешней силы. Возможно силовое воздействие, которое меняет обобщённые координаты, либо параметрическое, когда меняются параметры системы. Возможно и смешанное воздействие, как на обобщённые координаты, так и на параметры системы.
4.1. Вынужденные колебания в линейной системе при гармоническом воздействии
Для линейных стационарных систем выполняется принцип суперпозиции: если воздействие x1(t) порождает реакцию u1(t), а воздействие x2(t) реакцию u2(t), тогда воздействие, которое является линейной комбинацией первых двух a1x1(t) + a2x2(t) порождает следующую реакцию a1u1(t) + a2u2(t). Этот принцип означает, что в таких системах отсутствует нелинейное взаимодействие колебаний, вызванных различными одновременными действующими внешними силами. Будем считать, что собственные колебания в диссипативной системе достаточно быстро затухают, и можно анализировать только вынужденные колебания, т. е. рассматривать установившийся режим
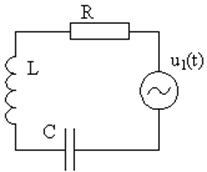
Рассмотрим простейший RLC контур с источником гармонического воздействия u1(t) с частотой w1 (рис. 26), тогда колебательный процесс будет описываться линейным ДУ:
|
Рис. 26. Колебательный контур с вынуждающей силой |
|
(4.1) |
|
Решением неоднородного ДУ (4.1) является сумма решений однородного уравнения, т. е. собственных колебаний, и частного решения неоднородного уравнения, т. е. вынужденных колебаний. Собственные колебания описываются уравнением (3.23)
|
Начальную фазу надо отсчитывать от внешнего воздействия. При гармоническом воздействии внешней силы реакция линейной системы есть гармонический сигнал:
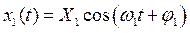 .
.
Подставим это выражение в (4.1):
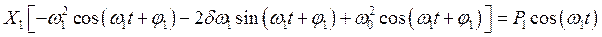 .
.
Воспользовавшись равенством
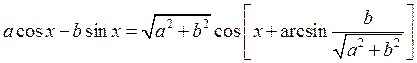 ,
,
преобразуем получившееся уравнение к виду
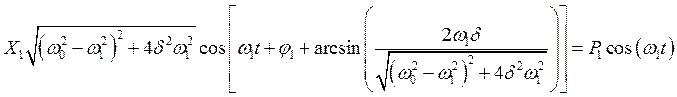 .
.
Приравнивая амплитуды и фазы в правой и левой частях этого уравнения, получим
|
|
(4.2) |
Мы обозначили g = w1/w0 — расстройка, Q0 = w0L/R — добротность. Из (4.2) следует, что j1(w1 ® 0) = 0, j1(w1 = w0) = p/2, j1(w1 ® ¥) = p.
Решим эту задачу методом комплексных амплитуд. Сопоставим току и напряжению их комплексные амплитуды, а также вспомним реактивные сопротивления, тогда можно записать
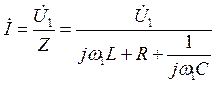 .
.
Найдём модуль
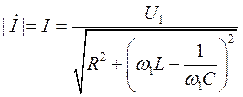 .
.
Нетрудно видеть, что максимальное значение тока:
![]() .
.
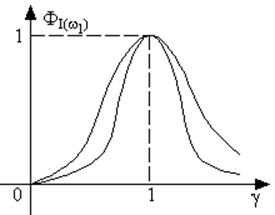
Введём форм-фактор, который определяет семейство нормированных резонансных кривых (в данном случае для тока)
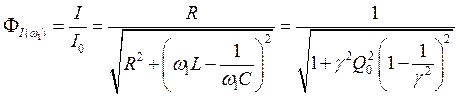 .
.
График этой функции приведён на рис. 27. Напряжение на резисторе пропорционально току через контур uR = iR, т. е. амплитуда напряжения на резисторе достигает максимума при w1 = w0. Зависимость фазы напряжения на резисторе от расстройки приведена на рис. 28.
|
Рефераты по физике сдают здесь
Другие статьиПохожая информацияУзнать стоимость за 15 минут
Распродажа дипломных
Подпишись на наш паблик в ВК
Нужна работа?
|