Закон сохранения энергии для свободной частицы
![]()
Для свободной частицы функция Лагранжа может зависеть от ряда скалярных произведений — инвариант, как то ![]() (I),
(I), ![]() (II),
(II), ![]() (III). В первом случае функция Лагранжа зависит от того или иного места в пространстве, то есть нарушается принцип однородности пространства. Во втором случае входит скалярное произведение
(III). В первом случае функция Лагранжа зависит от того или иного места в пространстве, то есть нарушается принцип однородности пространства. Во втором случае входит скалярное произведение ![]() , что приводит к тому, что функция Лагранжа зависит от угла между
, что приводит к тому, что функция Лагранжа зависит от угла между ![]() и
и ![]() , что в свою очередь означает нарушение принципа изотропности пространства. Таким образом, из этих трех инвариантов мы можем взять только
, что в свою очередь означает нарушение принципа изотропности пространства. Таким образом, из этих трех инвариантов мы можем взять только ![]() . Возьмем функцию Лагранжа в виде:
. Возьмем функцию Лагранжа в виде:
![]()
чтобы размерность совпадала с размерностью энергии. Коэффициент  мы взяли для удобства, хотя это можно было и не делать. Подставив полученную формулу в уравнение Эйлера-Лагранжа (2.3.7), можно получить
мы взяли для удобства, хотя это можно было и не делать. Подставив полученную формулу в уравнение Эйлера-Лагранжа (2.3.7), можно получить
![]()
Следовательно, мы получили
![]()
откуда вытекает закон сохранения энергии для свободной частицы:
![]()
Если же частицу (или заряд) поместить во внешнее поле, то вид функции Лагранжа усложнится. В нее войдут функция Лагранжа ![]() , описывающая движение свободной частицы, и
, описывающая движение свободной частицы, и ![]() , описывающая взаимодействие частицы (заряда) с полем:
, описывающая взаимодействие частицы (заряда) с полем:
![]()
По-прежнему, ![]() определяется выражением
определяется выражением 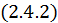 , тогда как
, тогда как ![]() берем в виде:
берем в виде:
![]()
Таким образом, общая функция Лагранжа будет выглядеть как
![]()
где ![]() есть четырехмерный потенциал.
есть четырехмерный потенциал.
В этом случае частные производные функции Лагранжа будут иметь следующий вид:

Таким образом, уравнение Лагранжа запишется как
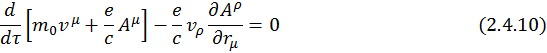
Взяв соответствующие производные и вспомнив, что четырехмерный вектор ускорения есть 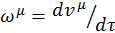 , получим:
, получим:
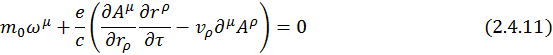
Наконец, воспользовавшись тем фактом, что ![]() , запишем
, запишем
![]()
Выражение слева есть ни что иное как сила, а скобка в правой части есть определения тензора электромагнитного поля ![]() . Таким образом, было получено выражение для силы, являющейся представлением силы Лоренца, которое имеет вид
. Таким образом, было получено выражение для силы, являющейся представлением силы Лоренца, которое имеет вид
![]()
§ 2.5. Релятивистские уравнения Гамильтона
Уравнения Гамильтона в классической механики имеют вид:
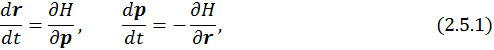
где r и p – независимые канонические переменные.
Функция Гамильтона в классической механике без учета электромагнитных полей:
![]()
Если взять производные по времени от канонических переменных, то получим нерелятивистскую скорость и нерелятивистскую, ньютоновскую силу. Покажем это:
![]()
Можно получить второй закон Ньютона из уравнений Гамильтона:
![]()
Таким образом, релятивистские уравнения Гамильтона имеют вид:
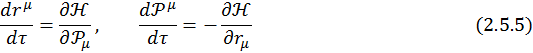
Следует отметить, что здесь ![]() и
и ![]() — "новые" функция Гамильтона и канонический импульс. И следует убедиться, что данные уравнения совпадают с теми, которые были определены ранее.
— "новые" функция Гамильтона и канонический импульс. И следует убедиться, что данные уравнения совпадают с теми, которые были определены ранее.
В нерелятивистском случае функцию Гамильтона для одной частицы можно было записать как
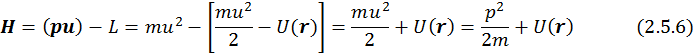
В релятивистском же приближении "новую" функцию Гамильтона следует записывать как
![]()
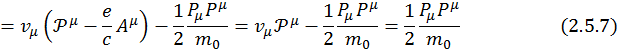
Таким образом,

Если подставить это уравнение в 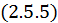 , то как раз получим силу Лоренца:
, то как раз получим силу Лоренца:
![]()
Таким образом, мы показали, что силу Лоренца можно также вывести из релятивистских уравнений Гамильтона.
Глава III
ПОЛЕВАЯ ЭЛЕКТРОДИНАМИКА
§ 3.1. Первая пара уравнений Максвелла в дифференциальной форме
Принято считать, что первая пара уравнений Максвелла не имеет самостоятельного значения. Эти уравнения нельзя рассматривать как уравнения движения поля. Это объясняется тем, что уравнения первой пары являются следствием определений напряженностей полей через потенциалы.


