Двумерная плоская задача ту
12.) Двумерная плоская задача ТУ.
А.)Плоская деформация.
Деформация называется плоской, если перемещения всех точек тела могут происходить только в двух направлениях в одной плоскости и не зависят от координаты, перпендикулярной к этой оси.
Примером плоской деформации может служить напряженно – деформированное состояние, возникающее в длинной прямой плотине или длинном своде подземного тоннеля.
Напряжение:
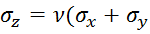 )
)
Дифференциальные уравнения равновесия Навье:
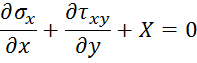
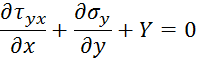
Условия на поверхности:
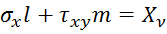
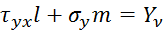
l, m – направляющие косинусы внешней нормали ![]() к поверхности контура
к поверхности контура 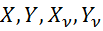 – компоненты объемных сил и интенсивности внешних поверхностных нагрузок на оси x и y
– компоненты объемных сил и интенсивности внешних поверхностных нагрузок на оси x и y
Уравнения Коши:
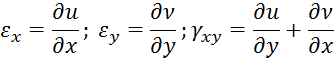
Уравнения неразрывности деформация Сен–Венана:
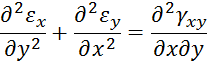
Формулы закона Гука:
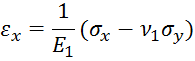
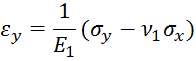
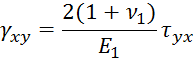
Упругие постоянные для закона Гука:
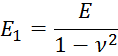
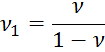
Б.)Обобщенное плоское напряженное состояние.
Плоское напряженное состояние возникает в том случае, когда длина тела мала, по сравнению с двумя другими размерами. В этом случае она называется толщиной. Напряжения в теле действуют только в двух направлениях в координатоной плоскости xOy и не зависят от координаты z. Примером такого тела пожжет служить тонкая пластина толщиной h, нагруженная по боковой поверхности силами, параллельными плоскости пластины и равномерно распределенными по ее толщине.
Напряженное состояние в пластине:
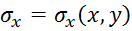
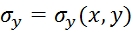
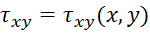
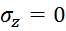
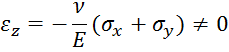
Основания пластины будут искривляться, так как появляются перемещения по оси z:
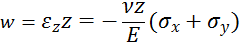
Основные уравнения плоской деформации: дифференциальные уравнения равновесия, условия на поверхности, уравнения Коши и уравнения неразрывности деформаций сохраняют такой же вид.
Формулы закона Гука примут следующий вид:
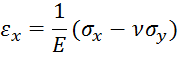
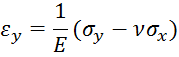
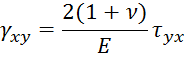
Изменятся только значения постоянных.
В плоской задаче теории упругости восемь неизвестных:
–две компоненты вектора перемещений ![]() и u
и u
–три компоненты тензора напряжений ![]() ,
, ![]() ,
, ![]()
–три компоненты тензора деформаций ![]() ,
,![]() ,
,![]()
Для решения задачи используют восемь уравнений:
–три уравнения Коши
–три формулы закона Гука
–два дифференциальных уравнения равновесия.
Кроме того, полученные деформации должны подчиняться уравнению неразрывности деформаций, а на поверхности тела должны выполняться условия равновесия.
В.)Решение плоской задачи ТУ в перемещениях.( http://www. strmech. susu. ac. ru/sopromat-file/BookIkr/BookIkr. pdf стр.323)
С помощью равенства 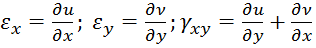 исключим деформации из уравнений
исключим деформации из уравнений 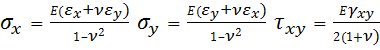 .
.
Полученные уравнения подставим в 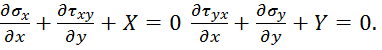
Полученные уравнения являются условиями равновесия, записанными в перемещениях.
Определив перемещения из полученных уравнений, напряжения и деформации можно найти из уравнений, полученных ранее, дифференцируя соответствующим образом функции u и v.
Г.) Решение плоской задачи ТУ в напряжениях. Уравнение Леви.
Решение плоской задачи в напряжениях сводиться к отысканию трех неизвестных функций:
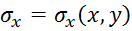
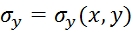
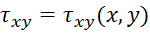
Подставляем в уравнение 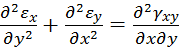 выражения деформаций из закона Гука
выражения деформаций из закона Гука 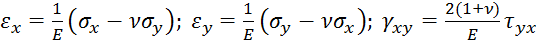
С помощью уравнения равновесия 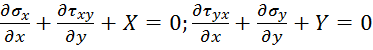 исключим из полученного уравнения касательное напряжение
исключим из полученного уравнения касательное напряжение ![]() .Для этого дифференцируем первое из уравнений по x, а второе по y, затем их складываем и получаем:
.Для этого дифференцируем первое из уравнений по x, а второе по y, затем их складываем и получаем:
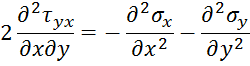
Подставляя выражение для смешанной производной от касательного напряжения ![]() в полученное уравнение, получаем условие неразрывности деформаций, записанное через нормальные напряжения:
в полученное уравнение, получаем условие неразрывности деформаций, записанное через нормальные напряжения:
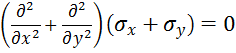
Это уравнение, полученное для плоского напряженного состояния, носит название уравнения Мориса Леви. Уравнения равновесия вместе с граничными условиями и уравнением неразрывности дают систему уравнений, которых достаточно для полного определения напряжений.


