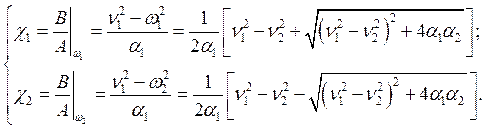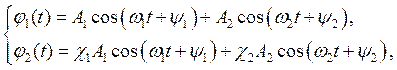Автоколебательные системы с внешним воздействием
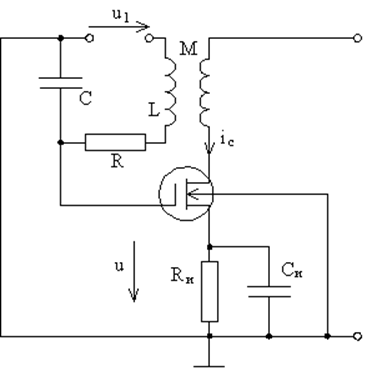
Рассмотрим пример, когда нелинейный элемент включен в цепь обратной связи (рис. 51). Схема
подобна схеме, изображённой на рис. 43, но теперь в резонансный контур включен термистор.
Пусть через термистор течёт синусоидальный ток i(t) = I0cos(w1t), тогда уравнение теплового баланса термистора принимает вид
|
|
(6.12) |
где m — масса термистора, c — его удельная теплоёмкость, k — коэффициент теплопроводности. Решение этого уравнения имеет следующий вид:
|
|
(6.13) |
где t = mc/k называется тепловой постоянной времени термистора, j — начальная фаза.
Из (6.13) следует, что в установившемся режиме (при t ® ¥) температуру термистора можно представить как сумму постоянной и переменной составляющих:
![]() .
.
Относительные пульсации температуры, т. е. отношение амплитуды переменной составляющей температуры к её постоянной составляющей, получаем из уравнения (6.13):
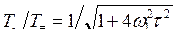 .
.
Этими вариациями температуры можно пренебречь, если w1 >> 1/t, тогда
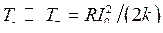 .
.
Таким образом, температуру термистора можно считать практически постоянной и пропорциональной квадрату амплитуды тока через него. Следовательно, можно считать, что сопротивление термистора зависит от амплитуды тока, а не от его мгновенного значения.
Уравнение (6.8) для генератора с термисторной стабилизацией амплитуды принимает вид
|
|
(6.14) |
где U — амплитуда установившихся колебаний. Соответственно, условие установившегося режима (6.9) можно переписать в виде:
|
|
(6.15) |
6.4. Автоколебательные системы с внешним воздействием, синхронизация колебаний
|
Рис. 52. Неавтономный генератор. |
Рассмотрим внешнее воздействие на томпсоновский генератор с контуром в цепи затвора (рис. 52). Пусть внешнее воздействие u1(t) = U1sin(w1t); напряжение на затворе выберем в качестве переменной u; тогда уравнение второго закона Кирхгофа для цепи обратной связи запишется в виде
Вводя безразмерные переменные x = u/u0, t = w1t, получим |
|
|
(6.16) |
|
где обозначено
|
Рассмотрим два случая.
1. Пусть коэффициент регенерации k < 0. Это означает, что точка покоя является устойчивой. В этом случае, имея в виду малую амплитуду возбуждаемых колебаний, характеристику ic = f(u) можно аппроксимировать на линейном участке характеристики линейной зависимостью ic = I0 + Su. Пусть воздействие w1 происходит вблизи резонансной частоты w0 (w1 » w0). Коэффициент k является почти таким же, как и для автономного генератора, тогда, как мы помним, условие k < 0 означает, что 2h > MSw0. Тогда уравнение (6.16) сводится к уравнению, которое описывает воздействие внешней силы на простейшую линейную систему (здесь в качестве такой системы выступает колебательный контур)
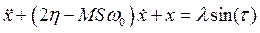 .
.
Как видно, положительная обратная связь уменьшает потери или, что эквивалентно, увеличивает добротность. Известно, что отклик системы на внешнее воздействие вблизи резонанса пропорционален добротности, т. е. положительная обратная связь увеличивает отклик системы. Такой режим работы автогенератора (недовозбуждённый, т. е. в отсутствие внешнего воздействия он ничего генерировать не будет) называется регенеративным или недовозбуждённым.
|
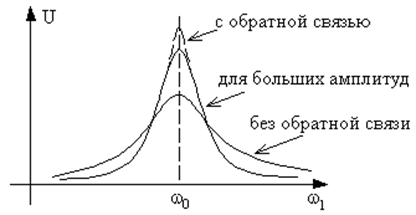
Рис. 53. Резонансные кривые регенерированного контура для немалых сигналов. |
При увеличении амплитуды внешнего воздействия нелинейностью функции ic = f(u) пренебрегать уже нельзя и использованная нами линейная аппроксимация ic = I0 + Su становится несправедливой. Резонансные кривые по-прежнему симметричны, но имеют немного иную форму, а именно несколько сплюснуты сверху в окрестности резонансного максимума из-за увеличения потерь в системе с ростом амплитуды колебаний. На рис. 53 приведён вид резонансных кривых при трёх случаях. |
2. Теперь рассмотрим случай, когда k > 0. По-прежнему будем считать, что w1 близка к резонансу, т. е. w1 » w0. Условие k > 0 означает, что 2h < MSw0. Тогда в отсутствии внешнего воздействия в системе появятся колебания с собственной частотой w тоже близкой к частоте резонанса. Поскольку автоколебательная система всегда нелинейная, то в системе произойдёт стабилизация амплитуды. Кроме того, на нелинейную систему воздействует ещё частота w1. За счёт нелинейного взаимодействия собственных колебаний с частотой w и вынужденных колебаний с частотой w1 в системе будут возникать колебания с комбинационными частотами вида |nw ± mw1|, где n и m — целые числа. Простейшие колебания, когда n = 1, m = 1, т. е. с частотой W = |w ± w1|, называют биениями.
В режиме самовозбуждения у генератора, описываемого уравнением (6.16), возможен очень важный для практики режим синхронизации колебаний, когда сравнительно маломощный источник внешнего воздействия задаёт частоту и фазу колебаний мощного генератора. Например, приложим к мощному генератору маломощное воздействие. Возможна ситуация, когда маломощный генератор, найдя свою частоту и фазу, навяжет эту частоту мощному генератору. Это и есть режим синхронизации колебаний. Так как теория довольно сложна, рассмотрим упрощённый случай. Пусть мощный генератор имеет мягкое возбуждение. Для произвольной характеристики усилителя ic = f(u), где f(u) какая-то нелинейная функция. Теперь уравнение (6.16) может быть переписано в таком виде:
|
|
(6.17) |
где обозначено
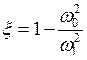 ,
, 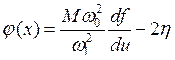 .
.
Если искать решение этого уравнения с частотой, точно равной частоте внешнего воздействия (t = w1t), то, используя обычную замену переменных в методе ММА
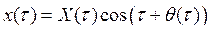 ,
, 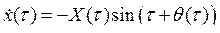 ,
,
укороченные уравнения примут вид:
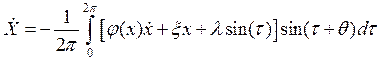 ;
;
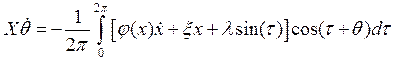 .
.
Подставляя значения ![]() и
и ![]() , получим
, получим
|
|
(6.18) |
Здесь функция D(X) описывает баланс потерь и вложения энергии, т. е. регенерацию (аналог колебательной крутизны). Для полевого транзистора, чью характеристику можно представить в виде ряда ic(u) = I0 + a0u + b0u2 + g0u3, получаем
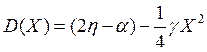 , где
, где 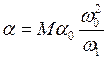 ,
, 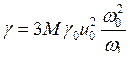 .
.
Вернёмся к уравнению (6.18). В автономном режиме генератора (l = 0) имеем
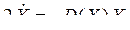 ;
; 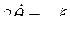 .
.
Найдём стационарные решения. Эти уравнения имеют два стационарных решения (![]() ,
, ![]() ): состояние покоя системы (X = 0), устойчивое при D(0) > 0 и неустойчивое при D(0) < 0, а также ненулевое решение X = X0 ¹ 0 (предельный цикл), где X0 определяется из равенства D(X0) = 0. Для фазы имеем: q = —xt/2 + q0. Учитывая, что w1 » w0, можно записать
): состояние покоя системы (X = 0), устойчивое при D(0) > 0 и неустойчивое при D(0) < 0, а также ненулевое решение X = X0 ¹ 0 (предельный цикл), где X0 определяется из равенства D(X0) = 0. Для фазы имеем: q = —xt/2 + q0. Учитывая, что w1 » w0, можно записать
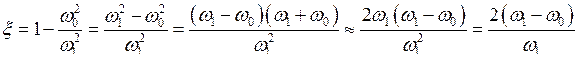 .
.
Взяв q = —xt/2, получим выражение
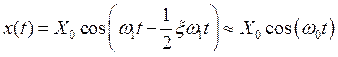 ,
,
которое подтверждает, что в автономном генераторе колебания происходят с собственной частотой системы w0, а не с частотой w1, с которой мы искали решение. Таким образом, мы видим, что использованный нами метод ММА исправил ошибку в определении частоты генератора.
Теперь рассмотрим неавтономный режим работы генератора (l ¹ 0) в области синхронизации. При D(0) < 0 (потери в системе превышают вложение энергии) в генераторе не выполняется условие самовозбуждения, однако имеет место регенерация, т. е. регенеративный режим. В этом случае получается несколько сплющенная сверху резонансная кривая (рис. 53).
При выполнении условия самовозбуждения генератора, т. е. D(0) > 0, синхронный режим работы томпсоновского генератора возможен лишь при малых значениях расстройки x (|x| << 1). В стационарном (![]() ,
, ![]() ) синхронном режиме из системы уравнений (6.18) получаем систему
) синхронном режиме из системы уравнений (6.18) получаем систему
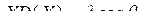 ;
; 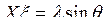 ,
,
или одно уравнение
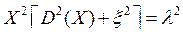 .
.
Решение такого уравнения непрерывно зависит от параметра. При произвольном D(X) последнее уравнение аналитически не разрешается. Можно ожидать, что при относительно малых значениях параметра l амплитуда колебаний почти такая же, как и в автономном режиме, т. е. X = X0. Таким образом, маломощный генератор навяжет частоту и фазу, но с амплитудой он ничего сделать не сможет (амплитуда является энергоёмким параметром, поэтому малое воздействие его энергию изменить не сможет, а вот частота и фаза на энергию не влияют). Итак, мы можем ожидать, что установившаяся амплитуда колебаний близка к стационарной амплитуде в автономном режиме, т. е. X » X0; тогда из второго уравнения (6.18) получаем соотношение
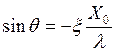 ,
,
которое имеет стационарное решение лишь при |x| £ x0 = l/X0. Это неравенство и определяет ширину полосы синхронизации: |w1 — w0| £ w1l/(2X0). Таким образом, чем слабее внешний генератор, тем точнее он должен быть подстроен в резонансную частоту. При расстройке, выходящей за пределы полосы синхронизации, присутствуют как вынужденные колебания на частоте w1, так и собственные колебания на частоте w0, следовательно, имеет место режим биений.
Рассмотрим поведение генератора при внешнем воздействии с большой амплитудой и частотой, почти кратной собственной частоте генератора w1 » nw0. Для удобства введём в рассмотрение такую частоту w, что w » w1/n » w0. Введём безразмерное время t = wt, нормированное на w, т. е. будем искать решение с частотой, близкой к частоте собственных колебаний системы. Если ввести расстройку 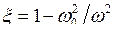 и аппроксимировать ток стока полиномом третьей степени ic(u) = I0 + a0u + b0u2 + g0u3, то, с учётом написанных выше соотношений, (6.17) можно записать в виде
и аппроксимировать ток стока полиномом третьей степени ic(u) = I0 + a0u + b0u2 + g0u3, то, с учётом написанных выше соотношений, (6.17) можно записать в виде
|
|
(6.19) |
где k = a — 2h, 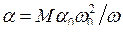 ,
, 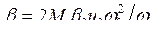 ,
, 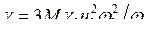 ,
, 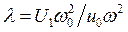 . Применение метода ММА для решения этого уравнения при |k| << 1, |b| << 1, |g| << 1, |x| << 1 и большом l требует перехода к новой переменной y(t), определяемой соотношением
. Применение метода ММА для решения этого уравнения при |k| << 1, |b| << 1, |g| << 1, |x| << 1 и большом l требует перехода к новой переменной y(t), определяемой соотношением
|
|
(6.20) |
где X1 — амплитуда вынужденных колебаний. Таким образом, решение уравнения (6.19) представляется в виде суперпозиции двух решений, причём член X1sin(nt) соответствует чисто вынужденному процессу колебаний с частотой внешнего воздействия, а член y(t) — колебаниям с частотой, близкой к собственной. Амплитуда X1 определяется условием X1 = l/(1 — n2). После подстановки (6.20) в (6.19) имеем
|
|
(6.21) |
Это уравнение уже допускает применение метода ММА, так как в правой части стоят малые члены. Ищем решение в виде
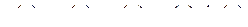 ,
, 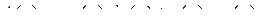
или, если для x:
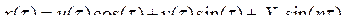 ,
, 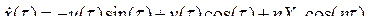 .
.
Рассмотрим случай n = 2; он представляет особый интерес, так как при этом значении n возникает так называемый резонанс второго рода. Укороченные уравнения принимают вид
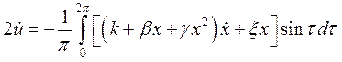 ;
;
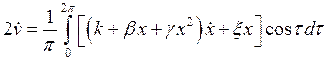 .
.
После интегрирования, получим
|
|
(6.22) |
Здесь z = u2 + v2, X1 = —U1/3.
Рассмотрим стационарные решения задачи ( ). Отличные от нуля стационарные состояния (u0 ¹ 0, v0 ¹ 0, z0 ¹ 0) легко получаются из системы (6.22).
). Отличные от нуля стационарные состояния (u0 ¹ 0, v0 ¹ 0, z0 ¹ 0) легко получаются из системы (6.22).
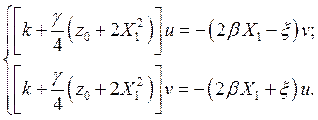
Отсюда видно, что
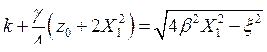 ,
,
откуда легко выразить z0:
|
|
(6.23) |
Знак "-" нас не интересует, так как z0 заведомо положителен.
|
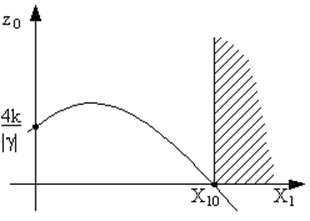
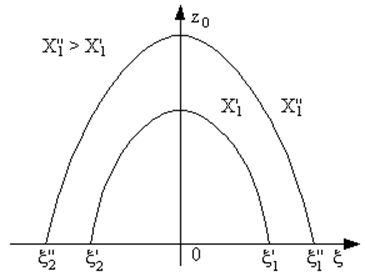
Попробуем формально построить график этого решения (рис. 54). При X1 ³ X10 физического смысла решение не имеет (заштрихованная область на рисунке). В зависимости от параметров рассматриваемой системы в ней может реализоваться несколько различных режимов. 1) В автономном режиме (U1 = 0, X1 = 0) стационарная амплитуда колебаний z0 = -4k/g существует при коэффициенте регенерации k > 0 (g < 0) и равна нулю (z0 = 0) при k < 0. Генерация колебаний происходит на собственной частоте w0. |
Рис. 54. График амплитуды автоколебаний при воздействии внешней силы с удвоенной частотой. |
2) В неавтономном синхронном (x = 0) режиме при внешнем воздействии (U1 > 0, X1 > 0) на автоколебательную систему (k > 0, g < 0) амплитуда автоколебательного процесса определяется из соотношения
|
|
(6.24) |
график которого мы и построили (рис. 54).
Мы сказали, что физический смысл имеют значения z > 0. Это значит, что если внешнее воздействие по амплитуде превосходит величину X10, происходит срыв автоколебаний, т. е. z0 становится равным нулю (z0 = 0). Происходит настолько мощное воздействие, что собственные колебания гасятся, а остаются только вынужденные колебания с частотой w1. Если X1 < X10, то амплитуда воздействия велика, но не слишком. Вот тогда (6.24) нормально существует, т. е. существует синхронный колебательный режим, когда в системе устанавливается частота вдвое меньшая (в данном случае), чем частота внешнего воздействия (резонанс первого рода). Это так называемый режим деления частоты.
3) Случай k < 0, g < 0, w ¹ w0 (x ¹ 0) соответствует недовозбуждённой автоколебательной системе с внешним воздействием на кратной частоте. При k < 0 собственных колебаний не будет, тогда z0 = 0. Положив в уравнении (6.23) z0 = 0, можно найти граничные значения расстройки, при которых возникают вынужденные колебания с частотой вдвое меньшей, чем частота внешнего воздействия (резонанс второго рода):
|
|
(6.25) |
Кривые резонанса второго рода z0(x) при разных значениях амплитуды внешнего воздействия показаны на рис. 55.
|
Рис. 55. Кривые резонанса второго рода. |
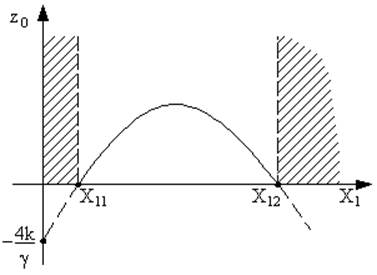
Рис. 56. Амплитудная кривая резонанса второго рода. |
Зависимость z0 от X1 имеет вид, изображённый на рис. 56.; кривая X11X12 показывает зависимость амплитуды вынужденных колебаний в недовозбуждённом генераторе от амплитуды внешнего воздействия на двойной частоте. В заштрихованной области имеет место вынужденный процесс с небольшой амплитудой из-за большого различия между собственной частотой системы w0 и частотой внешнего воздействия w1 (в нашем случае w1 » 2w0). Значение амплитуды внешнего воздействия, равное X11 называется порогом возбуждения, а значение X12 — потолком возбуждения. В области значений от X11 до X12 существует резонанс второго рода.
Тема 7. Колебательные системы с двумя степенями свободы
7.1. Парциальные системы и частоты, нормальные координаты и частоты
Любую колебательную систему с двумя степенями свободы можно представить как две системы с одной степенью свободы, связанные между собой. Из-за наличия этой связи колебания в одной системе влияют на колебания в другой системе, и наоборот. Такие системы, на которые можно разбить сложную колебательную систему, называются парциальными системами. Парциальная колебательная система описывается одной обобщённой координатой и получается из полной системы, если все остальные обобщённые координаты положить равными нулю. Частоты свободных колебаний парциальных систем называются парциальными частотами полной системы.
|
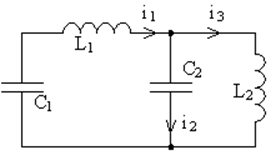
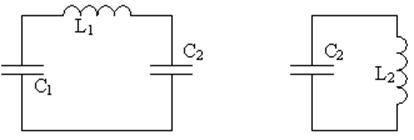
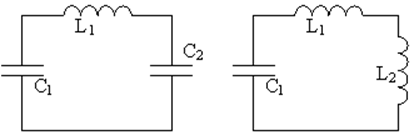
Разбиение полной системы на парциальные неоднозначно, поскольку независимые координаты могут быть выбраны различными способами. Так, например, в колебательном контуре, изображённом на рис. 57, в качестве независимых координат можно выбрать любую пару токов i1 и i2; i1 и i3 или i2 и i3, и тогда парциальные системы будут иметь вид, представленный на рис. 58. Соответственно меняются и парциальные частоты. Для независимых координат i1 и i2 они равны
для i1 и i3 —
для i2 и i3 —
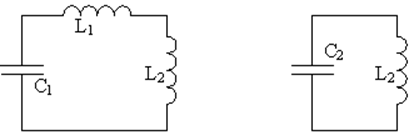
Характер связи между парциальными системами также зависит от выбора независимых переменных. На рис. 58, а связь индуктивная, 58, б — емкостная и 58, в — смешанная. В качестве независимых переменных в контуре на рис. 57, можно выбрать также напряжения на конденсаторах u1 и u2. В этом случае парциальные системы получаются при коротком замыкании конденсаторов C1 и C2. Соответствующие парциальные частоты равны
Физически ясно, что движение в полной системе при заданных начальных условиях будет одним и тем же, но запись его в различных координатах различна. |
Рис. 57. Схема электрического колебательного контура с двумя степенями свободы. а) б) в) Рис. 58. Различные варианты разбиения системы, показанной на рис. 57, на парциальные системы.
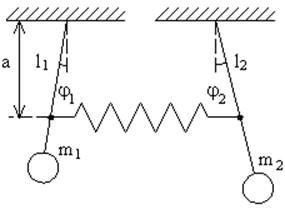
Рис. 59. Два связанных маятника. |
Теперь проведём изучение свободных колебаний в системе с двумя степенями свободы на примере двух маятников, связанных пружиной и совершающих колебания в плоскости рисунка (рис. 59).
Если углы отклонения маятников от положения устойчивого равновесия достаточно малы, то кинетическая и потенциальная энергии системы равны
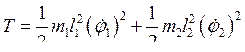 ,
,
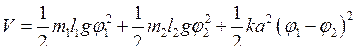 ,
,
где k — жёсткость пружины. Тогда уравнения движения системы (уравнения Лагранжа):
|
|
(7.1) |
|
|
(7.2) |
Получим уравнения колебаний парциальных систем. Положив в (7.1) j2 = 0, получим уравнение колебаний первой парциальной системы
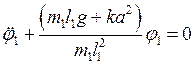
с собственной (парциальной) частотой n1:
|
|
(7.3) |
Из (7.2) при j1 = 0 получим выражение для второй парциальной колебательной системы
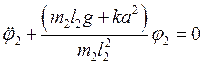
с парциальной частотой
|
|
(7.4) |
Если ввести коэффициенты связи 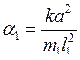 ,
, 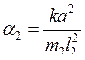 , то уравнения колебаний (7.1) и (7.2) принимают симметричный вид
, то уравнения колебаний (7.1) и (7.2) принимают симметричный вид
|
|
(7.5) |
Будем искать решение системы двух линейных дифференциальных уравнений (7.5) в виде гармонических колебаний
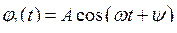 ,
, 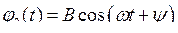
(фаза одинаковая, так как система без потерь). Подставляя решения в (7.5), получаем систему линейных алгебраических уравнений относительно амплитуд A и B:
|
|
(7.6) |
Система уравнений имеет нетривиальное решение, если её детерминант равен нулю, т. е. если
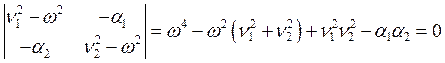 .
.
Решение полученного биквадратного уравнения даёт две возможные частоты колебаний системы:
|
|
(7.7) |
Частоты w1 и w2 не равны парциальным частотам n1 и n2 и называются собственными или нормальными частотами системы. Нормальные частоты системы не зависят от выбора координат. Они определяются только свойствами системы.
Если выполняется (7.7), то существуют нетривиальные решения системы (7.6), и тогда можно найти коэффициенты распределения амплитуд на нормальных частотах, т. е. на частотах w1 и w2:
|
|
(7.8) |
Таким образом, амплитуда колебаний одного из маятников на одной из нормальных частот может быть произвольной (она определяется начальными условиями). Амплитуда колебаний второго маятника на той же частоте всегда находится в определённом отношении к амплитуде колебаний первого маятника.
Общее решение уравнений (7.5) запишется в виде суммы гармонических колебаний с частотами w1 и w2:
|
|
(7.9) |
где постоянные A1, A2, y1 и y2 определяются начальными условиями.
Можно ввести нормальные координаты
|
|
(7.10) |
Какие бы начальные условия мы не задавали, нормальные координаты всегда совершают гармонические колебания со своей частотой. Координаты j1 и j2 связаны с нормальными координатами соотношением, которое следует из сравнения (7.9) и (7.10):
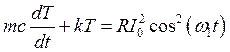 ,
,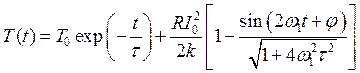 ,
,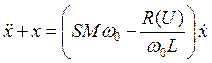 ,
,
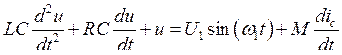 .
.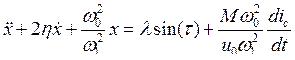 ,
,
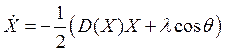 ;
;  .
.
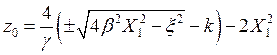 .
.
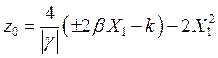 ,
,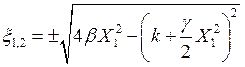 .
.
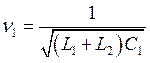 ,
, 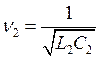
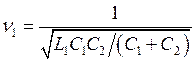 ,
, 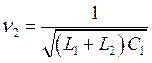 .
.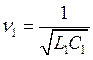 ,
, 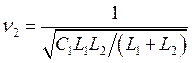 .
.
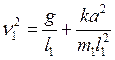 .
.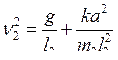 .
.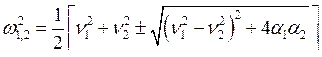 .
.