Взаимодействие тяжелых заряженных частиц с веществом
|
Взаимодействие тяжелых заряженных частиц |
Тяжелые заряженные частицы взаимодействуют главным образом с электронами атомных оболочек, вызывая ионизацию атомов. Максимальная энергия, которая может быть передана в одном акте взаимодействия тяжелой частицей, движущейся со скоростью v << с, неподвижному электрону, равна![]() Емакс = 2mev2.
Емакс = 2mev2.
Проходя через вещество, заряженная частица совершает десятки тысяч соударений, постепенно теряя энергию. Тормозная способность вещества может быть охарактеризована величиной удельных потерь dE/dx. Удельные ионизационные потери представляют собой отношение энергии ![]() Е заряженной частицы, теряемой на ионизацию среды при прохождении отрезка
Е заряженной частицы, теряемой на ионизацию среды при прохождении отрезка ![]() х, к длине этого отрезка. Удельные потери энергии возрастают с уменьшением энергии частицы (рис.1) и особенно резко перед ее остановкой в веществе (пик Брэгга).
х, к длине этого отрезка. Удельные потери энергии возрастают с уменьшением энергии частицы (рис.1) и особенно резко перед ее остановкой в веществе (пик Брэгга).
|
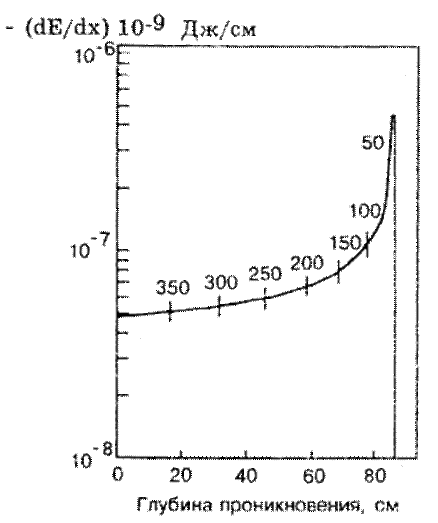
Рис. 2. Зависимость тормозной способности биологической ткани для протонов с начальной энергией 400 Мэв от глубины проникновения протонов в слой вещества. Численные значения над кривой — энергия протона (в МэВ) на различной глубине проникновения. В конце пробега — пик Брэгга. |
Если пролетающая через вещество частица имеет энергию большую, чем энергия связи электрона в атоме, удельные ионизационные потери энергии для тяжелых заряженных частиц описываются формулой Бете — Блоха
|
|
(1) |
где
mе — масса электрона (mес2 = 511 кэВ — энергия покоя электрона);
с — скорость света; v — скорость частицы; ![]() = v/c ;
= v/c ;
Z — заряд частицы в единицах заряда позитрона;
n — плотность электронов в веществе;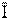 — средний ионизационный потенциал атомов вещества среды, через которую проходит частица.
— средний ионизационный потенциал атомов вещества среды, через которую проходит частица. 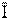 = 13.5 эB*Z’, где Z’ — заряд ядер вещества среды в единицах заряда позитрона;
= 13.5 эB*Z’, где Z’ — заряд ядер вещества среды в единицах заряда позитрона;
Удельные потери энергии пропорциональны числу электронов вещества и квадрату заряда частицы теряющей энергию на ионизацию. Удельные потери энергии не зависят от массы m проходящей через вещество частицы (при условии m >> me) но существенно зависят от скорости частицы. Например, мюоны гораздо тяжелее электронов, поэтому при той же энергии они теряют ее медленнее, чем электроны и проходят сквозь большие слои вещества без существенного замедления.
Для определенной среды и частицы с данным зарядом Z величина dE/dx является функцией только кинетической энергии: dE/dx = ![]() (E). Проинтегрировав это выражение по всем значениям Е от 0 до Еmax, можно получить полный пробег частицы, то есть полный путь R, который заряженная частица проходит до остановки и полной потери кинетической энергии:
(E). Проинтегрировав это выражение по всем значениям Е от 0 до Еmax, можно получить полный пробег частицы, то есть полный путь R, который заряженная частица проходит до остановки и полной потери кинетической энергии:
|
|
(2) |
Тяжелые заряженные частицы взаимодействуют в основном с атомными электронами. В частности вероятность ионизации атомов среды при энергиях альфа-частиц в несколько МэВ примерно в 103 раз больше вероятности ядерного взаимодействия. Взаимодействие альфа-частиц с ядрами вещества сводится к кулоновскому рассеянию на малые углы и поэтому они мало отклоняются от направления своего первоначального движения. Вследствие этого пробег тяжелой частицы R измеряют расстоянием по прямой от источника частиц до точки их остановки. Обычно пробег измеряется в единицах длины (м, см, мкм) или длины, умноженной на плотность (г/см2).
В одном акте ионизации в воздухе частица теряет около 35 эВ. Т. е., если начальная кинетическая энергия альфа-частицы равна 4 МэВ, то она полностью затормозится через 4·106/35![]() 105 актов ионизации.
105 актов ионизации.
Средний пробег Ra определяется как толщина слоя вещества, при прохождении которого поглощается половина частиц (см. рис.1). Иногда также используется понятие экстраполированного пробега Re. Он определяется с помощью экстраполяции по касательной к кривой пробега из точки, соответствующей поглощению половины частиц.
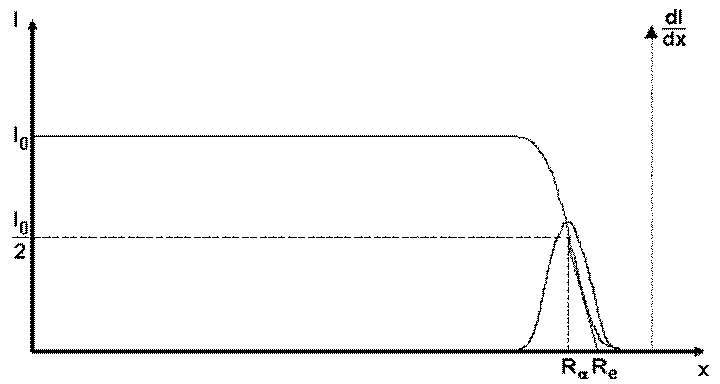
Рис. 1
Как видно из рис.1 пробеги имеют разброс около среднего (страгглинг), описываемый функцией Гаусса. Он обусловлен в частности статистическими флуктуациями ионизационных потерь. Действительно, если среднее число ионов, образуемое ![]() -частицей на длине ее пробега N, то среднеквадратичное отклонение от этого числа, будет N1/2. Кроме того, при прохождении через вещество
-частицей на длине ее пробега N, то среднеквадратичное отклонение от этого числа, будет N1/2. Кроме того, при прохождении через вещество ![]() -частица может испытать перезарядку, превращаясь в однозарядный ион гелия (4He+) или в атом гелия (4He). Разный заряд частицы на всем пути вызывает дополнительные флуктуации в ионизации и, следовательно, в пробеге. (По этой же причине по мере прохождения первоначально монохроматическими заряженными частицами слоя вещества возникает дисперсия по энергии)
-частица может испытать перезарядку, превращаясь в однозарядный ион гелия (4He+) или в атом гелия (4He). Разный заряд частицы на всем пути вызывает дополнительные флуктуации в ионизации и, следовательно, в пробеге. (По этой же причине по мере прохождения первоначально монохроматическими заряженными частицами слоя вещества возникает дисперсия по энергии)
Средний пробег Ra в воздухе при комнатной температуре (200)и нормальном давлении для альфа-частиц, испускаемых естественным изотопом, связан с энергией Ta эмпирической формулой
|
Ra (см) = 0.32 |
(3) |
Удельные ионизационные потери энергии в веществе со сложным химическим составом можно подсчитать по формуле
|
|
(4) |
где M — молекулярный вес соединения, Ni — количество атомов сорта i с атомным весом Ai в молекуле, (dE/d![]() )i — удельные потери для данного простого вещества.
)i — удельные потери для данного простого вещества.
УПРАЖНЕНИЕ 1
Определение толщин фольги по потерям энергии альфа-частиц
http://nuclphys. sinp. msu. ru/practicum/java/foils/index. html
Проградуируйте спектрометр. Для градуировки спектрометра вначале измеряется спектр альфа-частиц, испускаемых источником 226Ra, который содержит этот изотоп с продуктами его распада. Энергии альфа-частиц, образующихся при распаде изотопов, содержащихся в этом источнике 4.782, 5.305, 5.490, 6.002 и 7.687 МэВ (см. схему распада 226Ra). Постройте спектр. Идентифицируйте пики на спектре источника 226Ra. Найдите соответствие между номерами канала и энергиями альфа-частиц и постройте график зависимости энергии от номера канала (градуировочный график).
Используйте полученную зависимость для определения энергии альфа-частиц после их прохождения сквозь фольгу.
Толщина фольги R определяется по формуле
|
R = R0 — Rост, |
(1) |
где R0-пробег альфа частицы в веществе с начальной энергией, Rост — пробег альфа частиц в веществе с энергией оставшейся после прохождения данной фольги. Пробеги R рассчитываются по формуле (2) с помощью таблицы, в которой приведены необходимые данные: R(E) — длина пробега, S(E) — тормозная способность, D(E) — поправочный множитель.
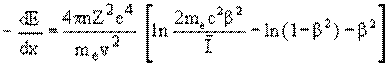
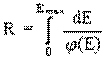
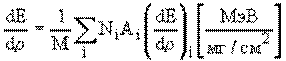 ,
,

