Начальные сведения об элементарных частицах
1.4.3 Эмульсионные камеры
Эмульсионные камеры представляют собой просто толстослойные фотопластинки. Это наиболее дешевые устройства. У них большая плотность рабочего вещества. Недостатком этих устройств является то, что следы ионизирующих частиц становятся видимыми только после проявления. Получается слишком большим время измерения.
1.4.4 Искровые камеры
Искровая камера является гибридом счетчика Гейгера и камеры Вильсона. В камере, заполненной газом при низком давлении, располагается система взаимно перпендикулярных электродов в виде тонких прямых проволок. В каждой из систем проводов, допустим в горизонтальных, между каждой последующей парой проводов включается разность потенциалов. При появлении ионного следа, оставляемого заряженной частицей, между электродами в местах появления ионов проскакивает искра. Электрические сигналы с пластин, возникающие из-за понижения разности потенциалов между пластинами при проскакивании искры, подаются на ЭВМ, которая восстанавливает траекторию частицы и анализирует ее.
Время измерения трековыми камерами определяется временем подготовки их к работе. Основным преимуществом искровой камеры является ее быстродействие. Недостаток — в сравнительно низком пространственном разрешении при восстановлении траектории.
В учебном кинофильме “Методы обнаружения и регистрации элементарных частиц” показаны основные методы регистрации элементарных частиц. Рекомендуем обсудить его.
2. Решение задач
Задача 1. Частица, пройдя ускоряющую разность потенциалов 4790 В, оставила в пузырьковой камере, помещенной в однородное магнитное поле B=0,1Тл, след в виде дуги окружности радиусом 10 см. Определите импульс частицы и ее инвариантную массу.
Решение. Предположим, что заряд частицы равен элементарному заряду e. В нерелятивистском пределе после ускорения энергия частицы равна 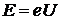 . Импульс частицы —
. Импульс частицы — ![]() . Учитывая это, получаем, что радиус кривизны траектории равен
. Учитывая это, получаем, что радиус кривизны траектории равен
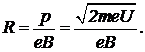 (1)
(1)
Рассматриваем выражение (1) как уравнение относительно неизвестной массы
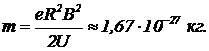 (2)
(2)
Из всех элементарных заряженных частиц только протон имеет такую массу.
Подстановка в выражение импульса дает p»1,6×10-21 кг м/с.
Задача 2. Два иона, прошедшие одинаковую разность потенциалов, влетели в однородное магнитное поле. Первый движется по окружности радиусом R1=3,6 см, второй — по дуге окружности R2=2,4 см. Определить отношение масс ионов, если заряд первого иона в два раза больше заряда второго.
Задача 3. Положительный пион (p+) имеет инвариантную массу 140 МэВ и среднее время жизни 2,6×10-8 с. Чему равна средняя длина треков между рождением и распадом пионов в пузырьковой камере при его энергии 280 МэВ? Чему будет равен радиус кривизны треков в магнитном поле индукции 2 Тл?
Задача 4. Заряженная частица с зарядом +e, родившаяся в водородной пузырьковой камере, имеет энергию 1010 эВ. Камера находится в магнитном поле индукции B=0,5 Тл. Частица оставила за собой трек длиной 2,2 см, который представляет собой дугу окружности радиуса
6,7 м, затем распалась. Определите собственное время жизни и инвариантную массу частицы (в МэВ).
4. Домашнее задание
4.1 Теоретический материал
Проработать материал занятия по пособию, своему конспекту. Дополнительно по учебнику Г. Я.Мякишева и Б. Б.Буховцева “Физика 11”. §76. Вариант: учебник “Физика 11” под ред. А. А.Пинского. §86.
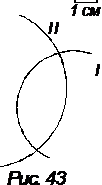 4.2 Решение задач
4.2 Решение задач
Задача 1. На рисунке, сделанном по фотографии, изображены следы двух частиц с одинаковыми зарядами, но разными массами. Частицы ускорены одной и той же невысокой разностью потенциалов и являются нерелятивистскими. Одна из частиц (I) — протон. Используя рисунок, определите массу другой частицы и сделайте предположение о том, какая это частица. Опишите в деталях процедуру определения массы.
Задача 2. Заряженная частица, с зарядом равным заряду протона, с инвариантной массой равной 1190 МэВ (сигма-плюс-гиперон) и кинетической энергией 9×109 эВ, родившаяся в водородной пузырьковой камере при столкновении двух протонов, оставила, до того как распалась, трек длиной 8 см. Чему равно собственное время жизни частицы? Чему равен радиус кривизны трека, если индукция магнитного поля, в котором находится камера, равна 5 Тл?
занятие 2.3.2
начальные сведения об элементарных частицах
2. Классификация элементарных частиц
2.1 Взаимодействия
Известны четыре фундаментальных взаимодействия, в которых могут участвовать частицы:
— гравитационное (универсальное взаимодействие, но самое слабое, в котором участвуют все частицы без исключения; оно является дальнодействующим, т. е. медленно спадающим с расстоянием);
— электромагнитное (участвуют частицы, обладающие электрическим зарядом или магнитным моментом, и фотоны; является дальнодействующим);
— слабое (участвуют все частицы, кроме фотонов; быстро спадает с расстоянием, по последним данным является одной из сторон электромагнитного взаимодействия);
— адронное (участвуют только адроны; быстро спадает с расстоянием).
Все многообразие природных процессов сводится к этим четырем взаимодействиям. Каждое из взаимодействий характеризуется быстротой спада с ростом расстояния.
Потенциальная энергия гравитационного и электрического взаимодействия спадает с расстоянием по степенному закону — 1/r. Такой закон называют дальнодействующим.
Приближенная формула потенциальной энергии двух адронновзаимодействующих нуклонов имеет вид: 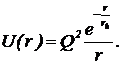 (1)
(1)
При каждом увеличении расстояния на rh числитель уменьшается в e раз. Этот факт и определяет большую скорость спадания U(r) с расстоянием. Множитель Q2 называют константой взаимодействия. Он играет ту же роль, что и ![]() для электрического взаимодействия. Параметр rh называют радиусом адронного взаимодействия. Формулу (1) впервые получил Юкава в 1935 году. Он получил следующее выражение для радиуса адронного взаимодействия:
для электрического взаимодействия. Параметр rh называют радиусом адронного взаимодействия. Формулу (1) впервые получил Юкава в 1935 году. Он получил следующее выражение для радиуса адронного взаимодействия:  , (2)
, (2)
где mp — инвариантная масса пиона.
Приближенная формула потенциальной энергии двух слабо взаимодействующих частиц имеет вид: 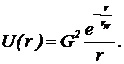 (3)
(3)
Множитель G2 — константа слабого взаимодействия. Радиус слабого взаимодействия rw на три порядка меньше радиуса адронного взаимодействия. Он равен 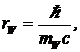 (4)
(4)
где mw — инвариантная масса промежуточного W-бозона. Она примерно в 90 раз больше массы протона.
Задача 1. Получите численные значения радиусов адронного и слабого взаимодействий.
Обменный механизм взаимодействия частиц, из которого следуют описывающие его формулы (1) и (3), является универсальными. Этот механизм применим не только к адронному и слабому взаимодействиям, но и к электромагнитному. Частицей-переносчиком электромагнитного взаимодействия является фотон. Поскольку инвариантная масса фотона равна нулю, постольку в соответствии с формулами (2) и (4) радиус электромагнитного взаимодействия оказывается равным бесконечности. А формула (1) превращается в 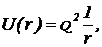 (5)
(5)
где Q2 — константа электромагнитного взаимодействия. Она равна ![]()
Константы взаимодействия имеют размерность [Дж×м]. Их значения зависят от выбора системы единиц. Чтобы иметь дело с величинами, не зависящими от выбора системы единиц, пользуются безразмерными константами взаимодействия: ![]() ,
, 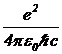 и
и ![]() . (6)
. (6)
Они примерно равны 1, 10-2, 10-1. Эти числа определяют отношение энергий взаимодействий.
Задача 2. Получите численное значение безразмерной константы электромагнитного взаимодействия: 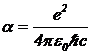 .
.


