Основы механики методичка
Настоящие Методические указания к выполнению вводной лабораторной работы по курсу «Основы механики. Молекулярная физика и термодинамика» представляют собой описание
ü регламента прохождения лабораторного практикума студентами всех специальностей и форм обучения,
ü а также правил проведения измерений в физпрактикуме
ü и порядка расчета погрешностей прямых и косвенных измерений.
Методические указания являются основой для выполнения лабораторных работ не только по курсу “Основы механики”, но и последующих разделов физики согласно учебного плана в технических университетах.
Составлено на основе ГОСов специальностей горно-нефтяного профиля.
Рекомендуется для выполнения студентами всех специальностей и форм обучения.
1. ОБЩИЕ УКАЗАНИЯ К ПРОВЕДЕНИЮ ЛАБОРАТОРНЫХ РАБОТ
Каждая лабораторная работа группой студентов в количестве до 2 человека. Темы лабораторных работ сообщаются студентам не менее чем за 2 недели до занятия.
Выполнение лабораторных работ и их защита оценивается по балльно-рейтинговой системе — (mах 6 баллов)[1].
Порядок получения допуска к лабораторной работе, выполнения ее и составления отчета заключается в следующем:
1. Согласно Списка литературы для подготовки к лабораторным занятиям (см. Приложение №1)
студенту необходимо самостоятельно ознакомиться с темой лабораторной работы, изучить теоретический материал по лекциям, учебнику и подготовить конспект (Правила конспектирования — Приложение 2).
2. В начале лабораторного занятия каждый студент (индивидуально!) в ходе собеседования с преподавателем защищает подготовленный дома теоретический материал, отвечает на контрольные вопросы устно (mах 3 балла),- и получает разрешение на подготовку к лабораторной работе по методическим указаниям к выполнению лабораторной работы (выдается лаборантом).
3. Для получения допуска к практическому выполнению лабораторной работы необходимо:
ü Подготовить бланк Отчета (см. Приложение №3).
ü Показать понимание сути физического явления, изучаемого в лабораторной работе.
ü Представлять цель и метод (техническое описание лабораторной установки) выполняемой лабораторной работы.
ü Твердо знать порядок выполнения лабораторной работы по пунктам (с указанием смысла каждого пункта действия)[2].
2. ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
Современная измерительная техника дает возможность делать измерения физических величин с большой точностью. Тем не менее, при измерениях неизбежны большие или меньшие ошибки (погрешности), зависящие от различных причин. В связи с этим при экспериментальном определении всякой физической величины возникают две задачи:
· провести измерения так, чтобы отклонения полученного значения измеряемой величины от истинного его значения было как можно меньше;
· дать оценку той погрешности, которая получилась при данном измерении.
Измерения физических величин распадаются на два класса: прямые и косвенные измерения.
К прямым измерениям относятся такие, которые выполняются приборами, проградуированными в единицах этой величины (примеры: измерения длин при помощи рулетки, плотности жидкостей при помощи спиртометра и т. п.).
Однако, чаще невозможно непосредственно измерить какую-либо физическую величину,- поэтому ее «измеряют» косвенно, рассчитывая ее через другие, доступные непосредственному измерению согласно некоей теоретической формуле (примеры: определение объема параллелепипеда через произведение длин ребер, плотности вещества через отношение массы к объему и т. п.).
Возникающие в процессе прямых измерений ошибки можно разбить на два вида: систематические и случайные.
Систематические ошибки вызываются несовершенством измерительных приборов или неправильным их использованием. Так, например, при взвешивании может получиться ошибка вследствие неравенства плеч коромысла весов; при определении температуры — вследствие смещения нулевой точки термометра, при определении длины масштабной линейкой — вследствие неточности ее делений. При пользовании данным измерительным прибором систематическое отклонение результата измерений от истинного значения величины будет всегда иметь один и тот же знак, сколько бы измерений ни делалось. Уменьшение систематических ошибок достигается путем тщательной выверки приборов и употреблением специальных приемов измерений.
Случайные ошибки являются результатом влияния случайных факторов, которые невозможно учесть (полностью исключить). В число этих факторов входят те неточности, которые вносит экспериментатор при наблюдении отсчетов по прибору. Случайные ошибки могут изменять результат в обе стороны, то увеличивая его, то уменьшая; один раз этот результат будет с “недомером”, другой раз с “перемером”. Заранее определить знак ошибки невозможно.
Случайные ошибки непосредственных измерений, не будучи в целом подчинены определенным законам, при большом числе измерений подчиняются статистическим законам. Учитывать и оценивать случайные погрешности можно при помощи методов теории вероятностей, один из разделов которой носит название “теории ошибок”.
Укажем на некоторые основные положения этой теории¨.
1. Если число измерений одной и той же величины очень велико, то для нахождения значения, как самой величины, так и для оценки точности ее значения, можно применять “законы больших чисел”
2. Наиболее достоверным (“истинным”) значением измеряемой величины является среднее арифметическое из результатов отдельных измерений.
3. При большом числе измерений положительные (+) и отрицательные (-) случайные ошибки, равные по абсолютной величине, встречаются одинаково часто.
4. Малые ошибки более вероятны, чем большие.
Необходимо подчеркнуть еще раз, что эти положения справедливы для очень большого числа измерений.
Тем не менее, перечисленные положения теории вероятностей приходится применять к измерениям в физическом практикуме, где число наблюдений обычно невелико. Отсюда получается очень важный вывод: чтобы результат измерения мало отличался от истинного значения определяемой величины, необходимо всякое физическое измерение выполнять возможно большее число раз.
2.1. Погрешности прямых измерений
2.1.1. Среднеарифметическое значение измеренной величины
Допустим, что измерение некоторой величины а проведено n раз. В результате этих измерений получены значения а1, а2, а3,.., аn.
Тогда ![]() среднеарифметическое значение равно:
среднеарифметическое значение равно:
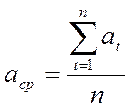 , (1)
, (1)
что является наиболее достоверным значением величины.
Полученный результат acp будет иметь меньшее отклонение от истинного значения измеряемой величины, чем каждое отдельное измерение, так как при суммировании ошибки в сторону “плюс” будут частично компенсироваться ошибками в сторону “минус”.
Количественная оценка ошибки измерения acp может быть сделана несколькими способами.
2.1.2. Средняя абсолютная ошибка
Отклонения результатов отдельных измерений от среднего арифметического acp, т. е. разности
½acp — аI ½= Dа1
½acp — а2½= Dа2 (2)
. . . . . . . . .
½acp — аn½= Dаn
называются абсолютными ошибками отдельных измерений.
Эти ошибки могут быть как положительными, так и отрицательными, но при оценке ошибки результата нас будут интересовать только их абсолютные значения.
Средней абсолютной ошибкой результата аcр называется среднее арифметическое абсолютных значений ошибок отдельных измерений, т. е.
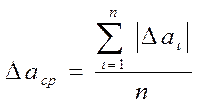 (3)
(3)
Так как вычисленные значения погрешностей с одинаковой вероятностью могут быть как положительными, так и отрицательными, то определить знак ошибки невозможно, поэтому, заканчивая измерения данной величины а, результат измерений записывают:
а = acp ± D аср (4)
что читается так: действительное (истинное) значение измеряемой величины а лежит в пределах:
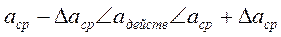 (5)
(5)
2.1.3. Относительная ошибка результата
Точность измерения характеризуется относительной ошибкой, которая представляет собою отношение абсолютной ошибки 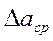 к результату измерения аcр:
к результату измерения аcр:


