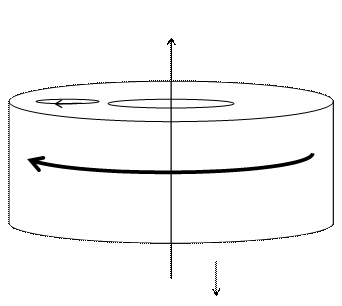
Поток напряженностей магнитного поля
![]()
Иногда поток напряженностей магнитного поля характеризуют в терминах числа линий напряженности. Это предполагает существование элементарного магнитного потока ![]() . Если каждому элементарному потоку сопоставить отдельную магнитную линию, то полный поток можно записать следующим образом:
. Если каждому элементарному потоку сопоставить отдельную магнитную линию, то полный поток можно записать следующим образом:
|
|
Тогда полный магнитный поток
А это означает, что число линий входящих равно числу выходящих линий, т. е. |
Долгое время представление об элементарном магнитном потоке было чисто умозрительным, придуманным для наглядности. Однако, в 1950 году англичанин польского происхождения Фритц Лондон предсказал квантование магнитного потока в сверхпроводящем кольце с током. В 1961 году Долл и Нойбауэр, а также независимо от них Дивер и Файербанк обнаружили экспериментально квантование магнитного потока. Рассмотрим теперь второе уравнение первой пары:
![]()
Для получения этого уравнения в интегральной форме, умножим его скалярно на элементарную площадку и проинтегрируем:
![]()
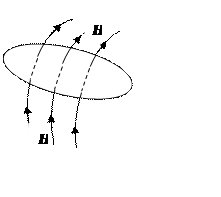
Из теоремы Стокса получим из поверхностного интеграла интеграл по замкнутому контуру, который ограничивает эту поверхность:
|
|
где |
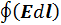 – криволинейный интеграл, который называется циркуляцией вектора напряженности электрического поля по замкнутому контуру. Отсюда вытекает закон Фарадея для магнитного потока (индукции).
– криволинейный интеграл, который называется циркуляцией вектора напряженности электрического поля по замкнутому контуру. Отсюда вытекает закон Фарадея для магнитного потока (индукции).
Умножим (3.5.7) на заряд ![]() , который будем считать единичным, и получим следующее выражение:
, который будем считать единичным, и получим следующее выражение:
![]()
Учтем, что 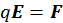 , получим
, получим
![]()
Здесь ![]() – элементарная работа по перемещению единичного заряда на участке
– элементарная работа по перемещению единичного заряда на участке ![]() , следовательно
, следовательно ![]() – электродвижущая сила:
– электродвижущая сила:
![]()
Мы пришли к закону Фарадея для электромагнитной индукции. Формально он гласит: при всяком изменении магнитного потока, пронизывающего некоторую поверхность, в замкнутом проводящем контуре, окаймляющем эту поверхность, возникает индукционный ток, который всегда имеет такое направление, что своим собственным магнитным полем препятствует изменению магнитного потока, вызвавшего данный ток. Это соотношение имеет глубокий физический смысл.
|
|
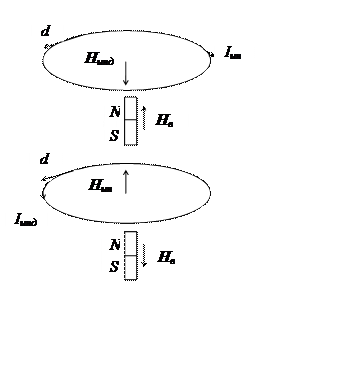
Рассмотрим постоянный магнит и контур. Если будем двигать магнит к контуру (рис. 3.5.4), в контуре возникнет индукционный ток, который будет направлен в противоположную сторону от Если будем двигать магнит от контура (рис.3.5.5), то магнитный поток ослабеет. Изменение магнитного потока отрицательно: |
Теперь рассмотрим неточечный заряд. Тогда
![]()
Умножим выражение (3.5.11) на ![]() , затем проинтегрируем и получим:
, затем проинтегрируем и получим:
![]()
Мы знаем, что 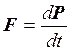 , где
, где ![]() – элементарный импульс.
– элементарный импульс.
![]()
Из постулата Бора следует, что циркуляция импульса по замкнутому контуру ( левая часть уравнения 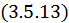 ) кратна целому числу n и равна
) кратна целому числу n и равна ![]() . Тогда
. Тогда
![]()
Минимальный магнитный поток соответствует n=1:

где q – заряд носителя тока.
|
Hвнеш I Hсверхпроводника |
Квантование магнитного потока наблюдалось в сверхпроводниках. Если мы хотим получить величину, соответствующую эксперименту нужно взять значение заряда носителя сверхпроводящего тока Рефераты по физике сдают здесь
Другие статьиПохожая информацияУзнать стоимость за 15 минут
Распродажа дипломных
Подпишись на наш паблик в ВК
Нужна работа?
|
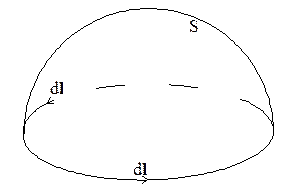
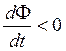 . Следовательно, ЭДС индукции вызовет ток
. Следовательно, ЭДС индукции вызовет ток