сопротивление материалов
Сопротивление материалов_1
V11: Сложное сопротивление
V2: Косой изгиб
V4: Напряжения в любой точке сечения
I:СМ_1 , КТ= 1, ТЕМА= «7.1.1.1.1»
S: Сложное сопротивление – это
-: действие на брус нескольких внешних сил
+: действие в каком-либо сечении бруса двух и более силовых факторов
-: действие в каком-либо сечении бруса одного силового фактора
-: действие на брус нескольких внешних сил и моментов
I:СМ_1 , КТ= 2, ТЕМА= «7.1.1.1.2»
S: Положение силовой плоскости при косом изгибе
-: совпадает с главной осью сечения
+: не совпадает с главной центральной осью сечения
-: совпадает с центральной осью сечения
-: не совпадает с центральной осью
I:СМ_1 , КТ= 3, ТЕМА= «7.1.1.1.3»
S: Косой изгиб показан на рисунках
 |
|
Рис. 1 |
Рис. 2 |
Рис. 3 |
Рис. 4 |
Рис. 5 |
-: 1
+: 2
+: 3
-: 4
-: 5
I:СМ_1 , КТ= 3, ТЕМА= «7.1.1.1.4»
S: Формула определения нормальных напряжений при косом изгибе в точках поперечного сечения:
-: 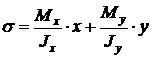
-: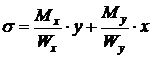
+: 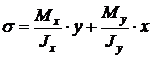
-: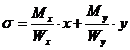
I:СМ_1 , КТ= 4, ТЕМА= «7.1.1.1.5»
 S: Напряжения в точке А бруса
S: Напряжения в точке А бруса
+: 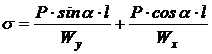
-: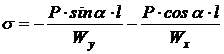
-: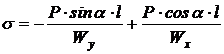
-: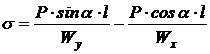
I:СМ_1 , КТ= 4, ТЕМА= «7.1.1.1.6»
 S: Напряжения в точке В бруса
S: Напряжения в точке В бруса
 |
-: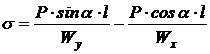
-: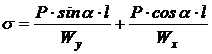
+: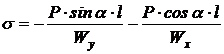
-: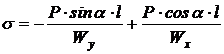
I:СМ_1 , КТ= 4, ТЕМА= «7.1.1.1.7»
S: Напряжения в точке C бруса
 |
-: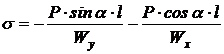
+: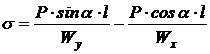
-: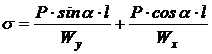
-: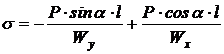
I:СМ_1 , КТ= 4, ТЕМА= «7.1.1.1.8»
S: Напряжения в точке D бруса
 |
-: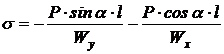
-: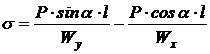
-: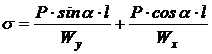
+: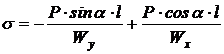
I:СМ_1 , КТ= 4, ТЕМА= «7.1.1.1.9»
S: Напряжения в точке K бруса
 |
-: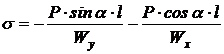
-: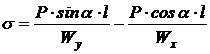
-: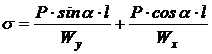
+: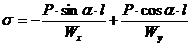
I:СМ_1 , КТ= 4, ТЕМА= «7.1.1.1.10»
S: Напряжения в точке E бруса
 |
+: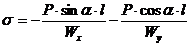
-: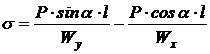
-: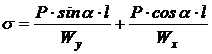
-: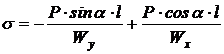
I:СМ_1 , КТ= 4, ТЕМА= «7.1.1.1.11»
|
S: Напряжения в точке M бруса
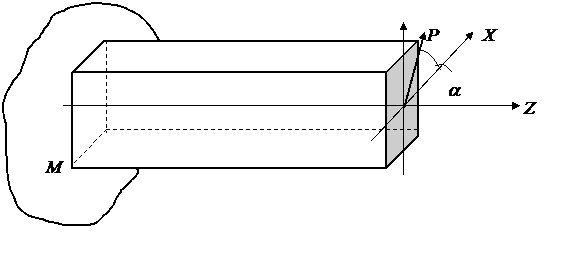 |
-: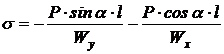
-: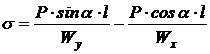
+: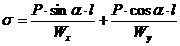
-: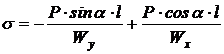
I:СМ_1 , КТ= 4, ТЕМА= «7.1.1.1.12»
S: Напряжения в точке N бруса
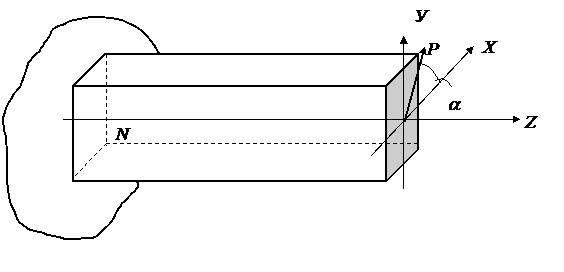
-: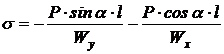
+: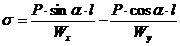
-: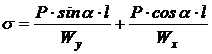
-: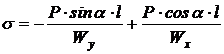
V4: Нейтральная линия
I:СМ_1 , КТ= 1, ТЕМА= «7.1.1.2.1»
S: Напряжения на нулевой (нейтральной) линии
-: нормальные напряжения экстремальны
+: нормальные напряжения равны нулю
-: действуют только касательные напряжения
-: касательные напряжения экстремальны
I:СМ_1 , КТ= 2, ТЕМА= «7.1.1.2.2»
S: Нейтральная линия при косом изгибе проходит
-: через точки на главных центральных осях, не совпадающие с центром тяжести
+: через центр тяжести поперечного сечения
-: по касательной к контуру поперечного сечения
-: по нормали к контуру поперечного сечения
I:СМ_1 , КТ= 3, ТЕМА= «7.1.1.2.3»
S: Нейтральная линия показана верно на рисунке
Рис. 1 |
Рис. 2 |
|
|
Рис. 3 |
Рис.4 |
-: 1
+: 2
-: 3
-: 4
I:СМ_1 , КТ= 3, ТЕМА= «7.1.1.2.4»
S: Положение нейтральной линии при косом изгибе определяется
+: с помощью углового коэффициента
-: по отрезкам, отсекаемым на координатных осях
-: по проекциям силы на главные оси
-: по проекциям изгибающего момента на главные оси
I:СМ_1 , КТ= 5, ТЕМА= «7.1.1.2.5»
S: Нейтральная линия перпендикулярна силовой линии в случаях:
+: главные осевые моменты инерции сечения равны между собой
+: при прямом изгибе
-: при растяжении и сжатии
-: центробежный момент инерции не равен нулю
I:СМ_1 , КТ= 2, ТЕМА= «7.1.1.2.6»
S: Напряжения в точках поперечного сечения, если нейтральная линия касается сечения
-: равны нулю
+: одного знака
-: разного знака
-: постоянны
I:СМ_1 , КТ= 2, ТЕМА= «7.1.1.2.7»
S: Напряжения в точках поперечного сечения, если нейтральная линия проходит вне сечения
-: равны нулю
+: одного знака
-: разного знака
-: постоянны
I:СМ_1 , КТ= 3, ТЕМА= «7.1.1.2.8»
S: Наиболее опасными на сечении являются точки
-: на нейтральной линии
+: наиболее удаленные от нейтральной линии
-: в центре тяжести поперечного сечения
-: на главных осях инерции
I:СМ_1 , КТ= 5, ТЕМА= «7.1.1.2.9»
 S: Угловой коэффициент нейтральной линии равен
S: Угловой коэффициент нейтральной линии равен
|
-: -: +: -: |
I:СМ_1 , КТ= 3, ТЕМА= «7.1.1.3.1»
S: Формула полного перемещения при косом изгибе:
 |
-: 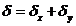
+: 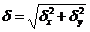
-: 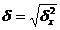
-: 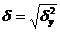
I:СМ_1 , КТ= 4, ТЕМА= «7.1.1.3.2»
S: Перемещение при косом изгибе по оси Х:
 |
-: 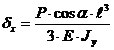
+: 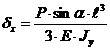
-: 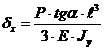
-: 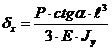
I:СМ_1 , КТ= 4, ТЕМА= «7.1.1.3.3»
S: Перемещение при косом изгибе по оси У:
 |
-: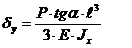
+: 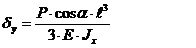
-: 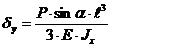
-: 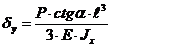
I:СМ_1 , КТ= 2, ТЕМА= «7.2.1.1.1»
S: Направление действия силы при внецентренном растяжение по отношению к продольной оси бруса
-: Перпендикулярно
+: Параллельно
-: Наклонно
-: Кососимметрично
I:СМ_1 , КТ= 3, ТЕМА= «7.2.1.1.2»
S: Точка приложения нагрузки при внецентренном растяжении не совпадает с # # # поперечного сечения
+: центром тяжести
I:СМ_1 , КТ= 2, ТЕМА= «7.2.1.1.3»
S:Внецентренное растяжение-сжатие эквивалентно
-: кручению с изгибом
-: двум поперечным изгибам
-: поперечному изгибу с центральным растяжением и сжатием
+: центральному растяжению-сжатию и двум чистым изгибам
I:СМ_1 , КТ= 1, ТЕМА= «7.2.1.1.4»
S: Вид сложного сопротивления бруса под действием силы Р:
 |
-: Кручение с изгибом
-: Сжатие
+: Внецентренное сжатие
-: Косой изгиб
I:СМ_1 , КТ= 3, ТЕМА= «7.2.1.1.5»
S: Формула для определения нормальных напряжений в произвольной точке К при внецентренном растяжении:
-: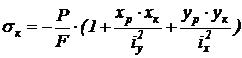
+: 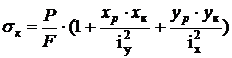
-: 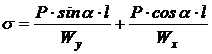
-: 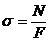
I:СМ_1 , КТ= 3, ТЕМА= «7.2.1.1.6»
S: Формула для определения нормальных напряжений в произвольной точке К при внецентренном сжатии:
-: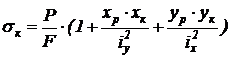
+: 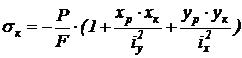
-: 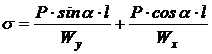
-: 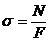
I:СМ_1 , КТ= 3, ТЕМА= «7.2.1.1.7»
((Q ВВОД 3 файл))
Величина Хк в формуле 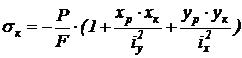 равна… см
равна… см
((V 1))
-1,5
I:СМ_1 , КТ= 3, ТЕМА= «7.2.1.1.8»
((Q ВВОД 3 ФАЙЛ))
Величина Ук в формуле 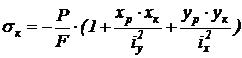 равна… см
равна… см

((V 1))
-3
I:СМ_1 , КТ= 4, ТЕМА= «7.2.1.1.9»
((Q ВВОД 4 ФАЙЛ))
Величина yр в формуле 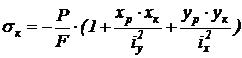 равна… см
равна… см

((V 1))
3
I:СМ_1 , КТ= 4, ТЕМА= «7.2.1.1.10»
((Q ВВОД 4 ФАЙЛ))
S: Величина Xр в формуле 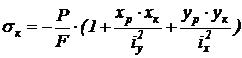 равна # # # см
равна # # # см
+: 1,5
I:СМ_1 , КТ= 4, ТЕМА= «7.2.1.1.11»
((Q ВВОД 4 ФАЙЛ))
S: Величина F в формуле 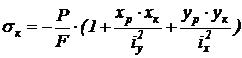 равна # # # см2
равна # # # см2
+: 18
I:СМ_1 , КТ= 3, ТЕМА= «7.2.1.2.1»
S: Символы Хр, Ур в уравнении нулевой линии 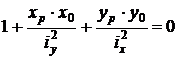 означают:
означают:
-: отрезки, отсекаемые нулевой линией на осях координат
+: координаты точки приложения силы
-: главные радиусы инерции поперечного сечения
-: размеры поперечного сечения
I:СМ_1 , КТ= 3, ТЕМА= «7.2.1.2.2»
S: Символы Х0, У0 в уравнении нулевой линии 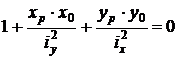 означают:
означают:
+: отрезки, отсекаемые нулевой линией на осях координат
-: координаты точки приложения силы
-: главные радиусы инерции поперечного сечения
-: размеры поперечного сечения
I:СМ_1 , КТ= 3, ТЕМА= «7.2.1.2.3»
S: Символы ix, iy в уравнении нулевой линии 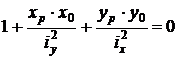 означают:
означают:
-: отрезки, отсекаемые нулевой линией на осях координат
-: координаты точки приложения силы
+: главные радиусы инерции поперечного сечения
-: размеры поперечного сечения
I:СМ_1 , КТ= 4, ТЕМА= «7.2.1.2.4»
S: Нейтральная линия поперечного сечения показана верно на рисунке:
|
|
+: 2 |
|
|
|
|
-: 1
+: 2
-: 3
-: 4
I:СМ_1 , КТ= 4, ТЕМА= «7.2.1.3.1»
S: Радиус ядра сечения круга # # # см
 |
+: 1
I:СМ_1 , КТ= 4, ТЕМА= «7.2.1.3.2»
S: Радиус ядра сечения круга # # # см

+: 2
I:СМ_1 , КТ= 4, ТЕМА= «7.2.1.3.3»
S: Радиус ядра сечения круга # # # см
 |
+: 5
I:СМ_1 , КТ= 4, ТЕМА= «7.2.1.3.4»
S: Радиус ядра сечения круга # # # см
 |
+: 8
I:СМ_1 , КТ= 4, ТЕМА= «7.2.1.3.5»
((Q ВВОД 4 ФАЙЛ))
Диагональ ядра сечения квадрата … см
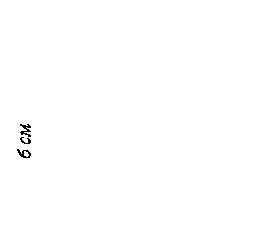
((V 1))
2
I:СМ_1 , КТ= 4, ТЕМА= «7.2.1.3.6»
((Q ВВОД 4 ФАЙЛ))
Диагональ ядра сечения квадрата … см
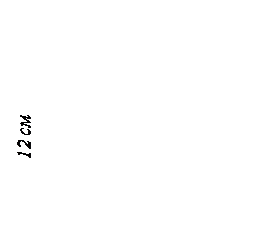
((V 1))
4
I:СМ_1 , КТ= 4, ТЕМА= «7.2.1.3.7»
((Q ВВОД 4 ФАЙЛ)
Диагональ ядра сечения квадрата … см
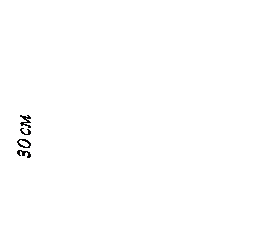
((V 1))
10
I:СМ_1 , КТ= 4, ТЕМА= «7.2.1.3.8»
((Q ВВОД 4 ФАЙЛ))
Диагональ ядра сечения квадрата … см
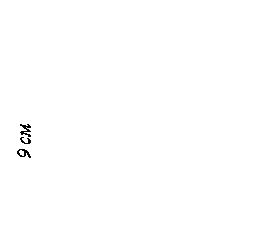
((V 1))
3
I:СМ_1 , КТ= 4, ТЕМА= «7.2.1.3.9»
((Q ВВОД 4 ФАЙЛ))
Диагональ ядра сечения квадрата … см

((V 1))
5
I:СМ_1 , КТ= 4, ТЕМА= «7.2.1.3.10»
((Q ВВОД 4 ФАЙЛ))
Меньшая диагональ ядра сечения прямоугольника… см

((V 1))
2
I:СМ_1 , КТ= 4, ТЕМА= «7.2.1.3.11»
((Q ВВОД 4 ФАЙЛ))
Меньшая диагональ ядра сечения прямоугольника… см

((V 1))
3
I:СМ_1 , КТ= 4, ТЕМА= «7.2.1.3.12»
((Q ВВОД 4 ФАЙЛ))
Меньшая диагональ ядра сечения прямоугольника… см

((V 1))
4
I:СМ_1 , КТ= 4, ТЕМА= «7.2.1.3.13»
((Q ВВОД 4 ФАЙЛ))
Меньшая диагональ ядра сечения прямоугольника… см

((V 1))
5
I:СМ_1 , КТ= 4, ТЕМА= «7.2.1.3.14»
((Q ВВОД 4 ФАЙЛ))
Меньшая диагональ ядра сечения прямоугольника… см
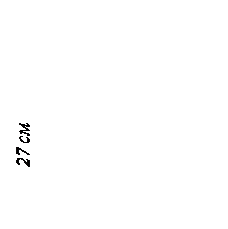
((V 1))
6
I:СМ_1 , КТ= 4, ТЕМА= «7.2.1.3.15»
((Q ВВОД 4 ФАЙЛ))
Меньшая диагональ ядра сечения прямоугольника… см

((V 1))
7
I:СМ_1 , КТ= 4, ТЕМА= «7.2.1.3.16»
((Q ВВОД 4 ФАЙЛ))
Большая диагональ ядра сечения прямоугольника… см

((V 1))
5
I:СМ_1 , КТ= 4, ТЕМА= «7.2.1.3.17»
((Q ВВОД 4 ФАЙЛ))
Большая диагональ ядра сечения прямоугольника… см

((V 1))
6
I:СМ_1 , КТ= 4, ТЕМА= «7.2.1.3.18»
((Q ВВОД 4 ФАЙЛ))
Большая диагональ ядра сечения прямоугольника… см

((V 1))
7
I:СМ_1 , КТ= 4, ТЕМА= «7.2.1.3.19»
((Q ВВОД 4 ФАЙЛ))
Большая диагональ ядра сечения прямоугольника… см

((V 1))
10
I:СМ_1 , КТ= 5, ТЕМА= «7.2.1.3.20»
S: Материал бруса, для которого необходимо строить ядро сечения при внецентренном сжатии
-: сталь
+: чугун
+: кирпич
+: камень
I:СМ_1 , КТ= 2, ТЕМА= «7.3.1.1.1»
S: Условие прочности при одновременном действии кручения и изгиба по третьей теории прочности
-:![]()
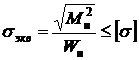
-: 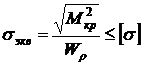
+: 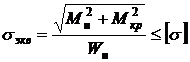
-: 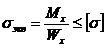
I:СМ_1 , КТ= 4, ТЕМА= «7.3.1.1.2»
S: Условие прочности при одновременном действии кручения и изгиба по четвертой теории прочности
-: 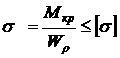
+: 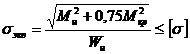
-:![]()
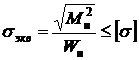
-: 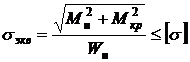




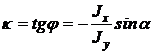
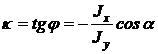
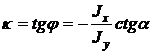

 -: 1
-: 1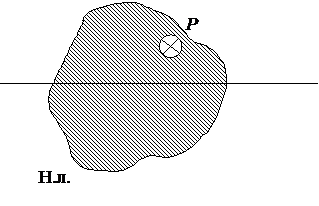

 -: 3
-: 3 -: 4
-: 4

