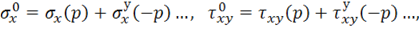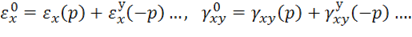теория пластичности

ЛЕКЦИЯ 13 ТЕОРИЯ ПЛАСТИЧНОСТИ. ВЫВОД ОСНОВНЫХ СООТНОШЕНИЙ

1 Пластические деформации

2 Обобщенные инвариантные характеристики напряженного и деформированного состояния

3 Анализ обобщенного закона Гука

4 Условия пластичности

5 Определение остаточных напряжений и деформаций

1 Пластические деформации

Как известно, закон Гука (1.11), которым описывается связь между напряжениями и деформациями, для большинства конструкционных материалов и, в частности, для металлических сплавов справедлив лишь до определенного уровня напряжений. Рассмотрим диаграмму деформирования материала, показанную на рисунке 1, которая может быть получена при растяжении образца. Линейная зависимость между напряжениями и деформациями (закон Гука) сохраняется до предела пропорциональности, характеризуемого ординатной точкой , при дальнейшем нагружении появляется площадка текучести , характеризуемая пределом текучести , а затем участок упрочнения материала .

Экспериментально установлено, что, если после нагружения до некоторой точки осуществить разгрузку, т. е. снизить напряжения до нуля, соответствующий участок разгрузки можно приближенно считать прямым и параллельным начальному участку активного нагружения . При этом в процессе разгрузки исчезает только часть развившейся деформации – упругая составляющая . Участок характеризует остаточную, пластическую деформацию, наличие которой является характерным признаком пластического поведения материала. Другим характерным свойством упругопластического деформирования является независимость кривой от времени нагружения образца.

Отчетливый горизонтальный участок текучести наблюдается далеко не у всех материалов, поэтому точка перехода из упругой области в пластическую является достаточно условной. В технических расчетах за предел текучести (или ) принимается напряжение, при котором остаточная деформация составляет . Это напряжение устанавливается как ордината точки пересечения экспериментальной кривой с прямой, параллельной участку , проходящей через точку с абсциссой .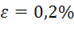

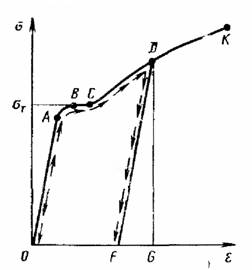
Рисунок 1

Расчет конструкций с учетом пластических деформаций материала является одной из основных задач науки о прочности летательных аппаратов. Для элементов, работающих в условиях интенсивного и кратковременного одноразового нагружения, появление пластических деформаций, как правило, считается допустимым и должно учитываться при расчете. В конструкциях, работающих многократно и в течение длительного времени, неупругое поведение материала, сопровождающееся образованием остаточных деформаций, обычно не допускается. Однако и в этом случае определение напряженно-деформированного состояния конструкции за пределом упругости, т. е. при нагрузках, превышающих эксплуатационные, позволяет установить предельную нагрузку, истинный запас прочности и возможный характер разрушений. Исключительно большое значение имеет анализ пластического поведения материалов для технических задач, связанных с приданием металлической заготовке необходимой формы за счет образования соответствующих остаточных деформаций.

Определение напряженно-деформированного состояния авиационных конструкций, работающих за пределом упругости (а также момента перехода в упругопластическое состояние), осуществляется с помощью уравнений прикладной теории пластичности, к выводу и анализу которых мы переходим. Прежде всего отметим, что соотношения теории пластичности так же, как и соотношения теории упругости, можно разделить на три группы – статические, геометрические и физические. При этом статические соотношения уравнения равновесия (1.9), записанные через функции напряжений, и геометрические соотношения (1.3), связывающие деформации с перемещениями, не зависят от свойств материала. Для построения теории пластичности необходимо получить физические соотношения, обобщающие закон Гука (1.11) на случай упругопластических деформаций.

2 Обобщенные инвариантные характеристики напряженного и деформированного состояния

Как следует из теории упругости, напряжения в любой точке тела определяются девятью компонентами, образующими тензор напряжений который в декартовых координатах записывается в виде

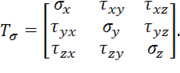
В силу закона парности касательных напряжений тензор напряжений симметричен относительно диагонали 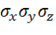. Для дальнейшего исключительно важное значение имеет понятие инвариантности. Дело в том, что компоненты тензора напряжений существенно зависят от направления осей координат, а переход материала в пластическое состояние в данной точке – явление объективное, которое не должно зависеть от того, в какую сторону мы направили оси. Поэтому напряжения, уровнем которых в итоге определяется переход материала за предел упругости, должны обладать некоторыми инвариантными комбинациями, сохраняющими постоянные значения в данной точке во всех системах, для которых эта точка является началом координат.

Тензор напряженного состояния, главные напряжение, а также вопросы, посвященные отысканию главных площадок и инвариантов напряженного состояния, были рассмотрены в лекции №2. Результаты приведем в виде основных тезисов:

ü Существуют такие положения площадок, когда касательные напряжения равны нулю, а нормальные – достигают экстремальных значений. Такие плоскости называют главными плоскостями напряженного состояния, а соответствующие нормальные напряжения – главными напряжениями.

ü Для отыскания положения главных плоскостей напряженного состояния необходимо решить характеристическое уравнение

корни которого дают три величины главных напряжений .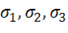

ü Коэффициенты 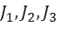не зависят от выбора направления осей и называются инвариантами напряженного состояния. Они определяются соотношениями

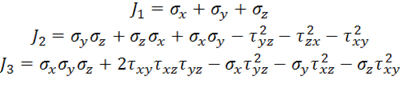
ü Максимальное касательное напряжение возникает в площадках, равнонаклоненных к главным площадкам, на которых действуют максимальное и минимальное главные напряжения. Его величина равна половине разности этих напряжений:

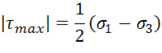
Как показывают экспериментальные исследования, нагружение металлов всесторонним гидростатическим давлением не вызывает остаточных деформаций. Для такого нагружения 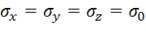и согласно (11.6), 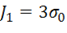. Ввиду того, что является инвариантом тензора напряжений, можно и в общем случае напряженного состояния ввести величину

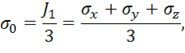
которая называется средним напряжением и характеризует составляющую тензора напряжений, вызывающую изменение объема материала. Эта составляющая не вызывает пластических деформаций и при построении теории пластичности целесообразно выделить ее из тензора напряжений. Проделаем это, представив тензор напряжений (11.1) в виде

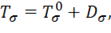
где

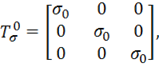
называется шаровым тензором, а

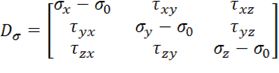
называется девиатором напряжений. По девиатору напряжений можно судить, насколько напряженное состояние в данной точке отличается от всестороннего равномерного растяжения или сжатия.

Для дальнейшего существенным является именно девиатор напряжений, поэтому рассмотрим его более подробно. Так же, как; и девиатор напряжений является тензором и имеет три инварианта, сохраняющих в данной точке постоянные значения при любых направлениях осей декартовой системы координат. Эти инварианты могут быть построены по формулам (11.7), если заменить в них на 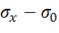и т. д. Исключая из полученных выражений с помощью равенства (11.14), окончательно будем иметь

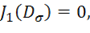
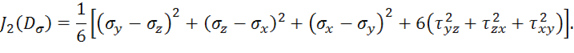
Инвариант в дальнейшем не потребуется и не приводится. В теории пластичности исключительно большую роль играет второй инвариант девиатора напряжений . С его помощью можно ввести некоторые обобщенные инвариантные характеристики напряженного состояния, например, величину

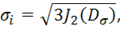
которая называется интенсивностью напряжений и в развернутой форме имеет вид

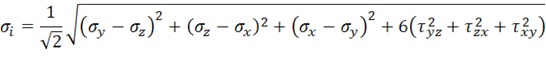
Численный коэффициент в формуле (11.19) подобран так, чтобы при одноосном нагружении значение интенсивности напряжений совпадало с величиной напряжений. Действительно, если все напряжения, кроме, например, 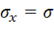, равны нулю, из (11.19) получим 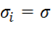. В принципе этот коэффициент может быть выбран произвольно, в том числе и так, чтобы обобщенное напряжение вырождалось в касательное напряжение при чистом сдвиге. Соответствующая обобщенная инвариантная характеристика напряженного состояния называется интенсивностью касательных напряжений и записывается в виде

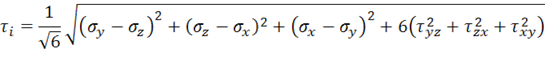
При чистом сдвиге, т. е. когда все напряжения, кроме, например 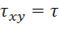, равны нулю, имеем .

Существенно, что напряжения и не зависят от направления осей координат, т. е. позволяют получить объективную характеристику напряженного состояния в данной точке. Этим же свойством обладают, как следует из изложенного выше, главные напряжения 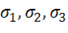и максимальное касательное напряжение .

Получим теперь аналогичные результаты для деформаций. Как следует из теории упругости, деформации так же, как и напряжения, образуют симметричный тензор, аналогичный (11.1), т. е.

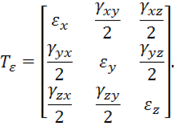
Этот тензор обладает тремя инвариантами, которые могут быть получены непосредственно из (11.7), если заменить :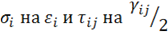

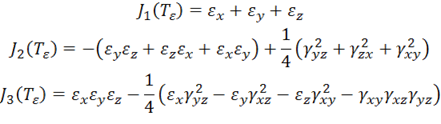
Для тензора деформаций так же, как и для тензора напряжений, существуют три главных направления, вдоль которых реализуются главные деформации 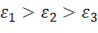. В системе координат, оси которой совпадают с главными направлениями, деформации сдвига равны нулю, т. е. главные направления в процессе деформирования остаются взаимно ортогональными. Аналогично (11.13) может быть найдена максимальная деформация сдвига,

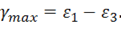
Выделим теперь из тензора деформаций составляющую, характеризующую изменение объема тела. Введем среднюю деформацию

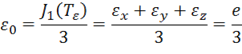
где – относительное изменение объема материала.

Тогда тензор деформаций аналогично (11.15) можно представить в виде

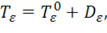
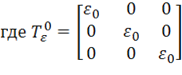– шаровой тензор, характеризующий изменение объема, а

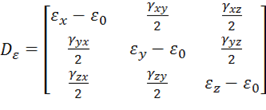– девиатор деформаций, характеризующий изменение формы тела. Инварианты девиатора деформаций записываются аналогично (11.17), т. е.

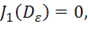
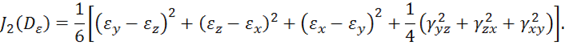
Третий инвариант здесь не приводится.

Образование и развитие пластических деформаций связано с напряжениями, вызывающими изменение формы тела. Поэтому в теории пластичности большую роль играет девиатор деформаций и особенно существенным является его второй инвариант. Аналогично понятию интенсивности напряжений (11.19) можно ввести величину интенсивности деформаций

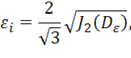
которая в развернутой форме имеет вид

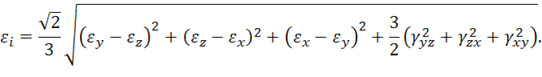
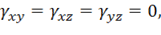
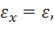
При нагружения вдоль оси имеем 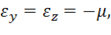(коэффициент Пуассона при упругопластическом деформировании не является постоянным и зависит от уровня напряжений). При этом из (11.26) получим

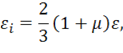
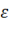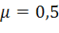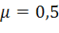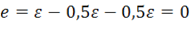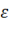В отличие от интенсивность деформаций вырождается при одноосном нагружении в деформацию лишь при . Такое значение коэффициента Пуассона имеет материал, объем которого при деформировании не изменяется. Действительно, при для одноосного нагружения согласно (11.22) имеем . Таким образом, вырождается в только для несжимаемого материала.

Аналогично интенсивности касательных напряжений (11.20) можно ввести интенсивность деформаций сдвига

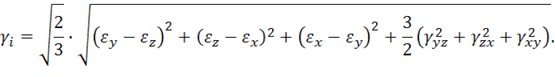
При чистом сдвиге, т. е. когда 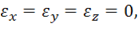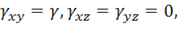получим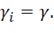

Таким образом, можно ввести обобщенные инвариантные характеристики деформированного состояния и не зависящие в данной точке от направления осей выбранной системы координат. Инвариантными являются также главные деформации 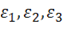и максимальная деформация сдвига (11.21).

3 Анализ обобщенного закона Гука

Выше были получены некоторые статические и геометрические соотношения, необходимые для построения прикладной теории пластичности. Прежде чем перейти к выводу соотношений, связывающих напряжения и деформации в теории пластичности, рассмотрим закон Гука, используемый в теории упругости. Представленный ниже анализ позволит в дальнейшем получить физические соотношения теории пластичности путем естественного обобщения закона Гука для линейно-упругого тела. Закон Гука имеет вид

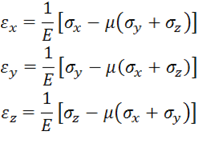
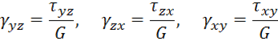
Складывая равенства (11.29) и вводя величину среднего напряжения и объемные меры деформаций согласно (11.14), (11.22), получим

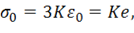
где 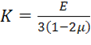– модуль объемной деформации.

Значение 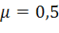соответствует несжимаемому материалу. Действительно, при 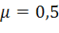имеем 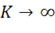. Кроме того, в этом случае .

Вычтем из левых и правых частей равенств (11.29) величину деформации . Выражая в правых частях через согласно (11.31), окончательно получим

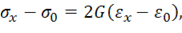
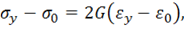
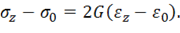
Добавляя к этим равенствам закон Гука для касательных напряжений (11.30), можно заключить, что компоненты девиатора напряжений (11.16), пропорциональны компонентам девиатора деформаций (11.23), т. е.

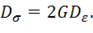
Установим связь между обобщенными инвариантными характеристиками напряженно-деформированного состояния, т. е. между 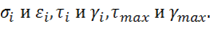Заменяя в правой части (11.19) функции напряжений через функции деформаций с помощью равенств (11.30), (11.32) и сравнивая полученное выражение с (11.26), будем иметь

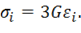
Для несжимаемого материала (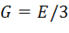) получим

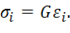
Преобразуя аналогичным образом выражение для (11.20), можно установить, что 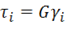. И, наконец, если записать соотношения (11.32) в главных осях, заменив на то вычитая третье равенство из первого, получим .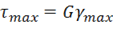

Таким образом, можно заключить, что для линейно-упругого тела девиатор напряжений прямо пропорционален девиатору деформаций и независимо от вида напряженного состояния интенсивность напряжений связана с интенсивностью деформаций единой зависимостью, аналогичной закону Гука для одноосного растяжения (для несжимаемого материала), а и связаны соответственно с и законом Гука для чистого сдвига.

В заключение анализа линейно-упругого материала получим еще один результат, который потребуется в дальнейшем. Запишем выражение для удельной потенциальной энергии деформации. Из (1.23) при имеем

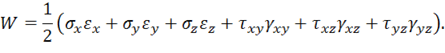
Выражая напряжения и деформации через (11.14), (11.22) и компоненты девиаторов (11.16), (11.23), после весьма громоздких преобразований, которые здесь опущены, окончательно получим

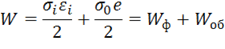
т. е. суммарная удельная энергия может быть разделена на две составляющие – энергию, накопленную в результате изменения формы тела (см. энергия формоизменения) и его объема.

4 Условия пластичности

Сформулируем критерий (условие пластичности), который позволит установить момент перехода материала в пластическое состояние. В случае одноосного растяжения этот вопрос решается просто – материал переходит в пластическое состояние, когда нормальное напряжение достигает предела текучести , определяемого экспериментально. Необходимо сформировать условие, которое позволит решить этот вопрос для произвольного напряженного состояния, имея в распоряжении лишь одну экспериментальную характеристику – . Ниже приводятся два наиболее распространенных условия пластичности.

Первое из них, называемое условием пластичности Треска – Сен-Венана (или просто условием Треска), было сформулировано в 70-х годах XIX века на основе экспериментальных исследований французского инженера Треска, который установил, что материал переходит в пластическое состояние, когда максимальные касательные напряжения достигают предела текучести при сдвиге , т. е. согласно равенству (11.13)

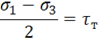
(см. также третье условие прочности)

При одноосном растяжении до предела текучести материала имеем 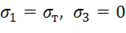, т. е. из (11.37) следует, что 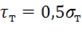и условие Треска можно записать в виде

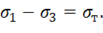
Отметим, что соотношение между пределами текучести при растяжении и сдвиге можно установить экспериментально. Для различных металлов при этом получается 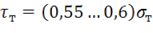, т. е. условие Треска удовлетворительно согласуется с экспериментом.

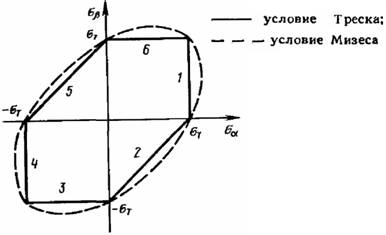
Рисунок 2 – Условия пластичности для плоского напряженного состояния

Рассмотрим геометрическую интерпретацию условия Треска. В пространстве напряжений (т. е. в системе координат, по осям которой отложены величины напряжений, действующие в данной точке) условие пластичности определяет некоторую поверхность, а напряженное состояние представляется точкой пространства. Если эта точка лежит внутри поверхности, определяемой условием пластичности, материал является упругим, если она лежит вне этой поверхности – упругопластическим.

Применительно к условию Треска исследуем случай плоского напряженного состояния (одно из главных напряжений равно нулю). Обозначим главные напряжения через 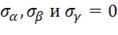, причем в зависимости от относительной величины напряжений индексы принимают значения 1, 2, 3. Введем систему координат, показанную на рисунке 2.

Предположим, что 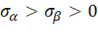, тогда 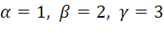, условие (11.38) записывается в виде 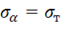и определяет отрезок 1 на рисунке 2. Если 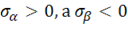, получим 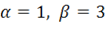, т. е. 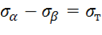(отрезок 2). Аналогично при 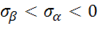получим прямую 3, при 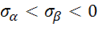– 4, при 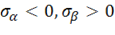– 5 и при 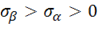– отрезок 6. В результате условие пластичности Треска изображается шестиугольником, показанным на рисунке 2. Проведенное построение иллюстрирует основной недостаток условия Треска – оно записывается относительно главных напряжений, которые необходимо предварительно определить, и его форма зависит от относительной величины и знака главных напряжений. Однако в тех случаях, когда направления и знаки главных напряжений известны заранее, условие Треска оказывается весьма эффективным, так как оно линейно относительно напряжений.

Второе условие пластичности носит название условия Мизеса – Губера – Генки (или просто условия Мизеса). Оно было сформулировано в начале XX века и может быть получено следующим образом. Пластическое деформирование связано в основном с изменением формы тела, объемная деформация является обратимой, т. е. упругой. В качестве инвариантной меры, характеризующей степень изменения формы, может быть принята введенная выше удельная энергия формоизменения . Согласно равенствам (11.36) и (11.34) в общем случае напряженного состояния имеем

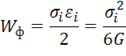
Естественно предположить, что материал переходит в данной точке в пластическое состояние, когда достигает некоторого критического значения , не зависящего от вида напряженного состояния, т. е. 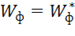. Величина может быть определена из опыта на одноосное растяжение. При этом 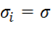и при достижении предела текучести 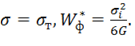Приравнивая 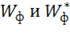, получим 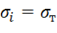или в развернутом виде с учетом выражения (11.19)

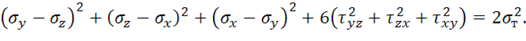
Соотношение (11.39) и является искомым условием пластичности. Для плоского напряженного состояния 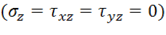условие пластичности Мизеса имеет вид

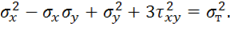
Для геометрической интерпретации условия Мизеса запишем его в главных напряжениях . Из (11.40) имеем

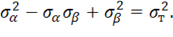
Уравнение (11.41) на плоскости () определяет эллипс, показанный пунктиром на рисунке 2.

Преимуществом условия Мизеса является то, что оно может быть записано в форме (11.39), (11.41) в произвольной декартовой системе координат. Для чистого сдвига при нагружении до предела текучести 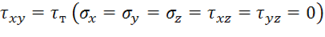из (11.39) имеем 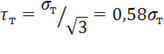. Сравнивая этот результат с экспериментальным – 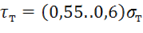, можно заключить, что условие Мизеса согласуется с экспериментом несколько лучше, чем условие Треска, для которого 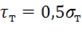. Однако, как следует из рисунка 2, различие между этими двумя условиями невелико и в практических расчетах используется, как правило, условие, с которым задача решается проще.

Помимо двух рассмотренных выше, можно сформулировать и другие, более сложные условия пластичности, причем все возможные варианты должны удовлетворять некоторым общим требованиям. Прежде всего условие пластичности должно устанавливать момент перехода материала в пластическое состояние в общем случае напряженного состояния и содержать экспериментальные параметры, которые могут быть найдены из простых опытов. Далее условие пластичности должно давать объективную информацию, не зависящую от принятой системы координат, т. е. оно должно быть записано через инвариантные характеристики напряженного состояния. И, наконец, поверхность, определяемая условием пластичности, должна быть выпуклой (т. е. отрезок прямой, соединяющей две любые точки поверхности, должен лежать внутри этой поверхности), а начало координат пространства напряжений должно находиться внутри этой поверхности.

Таким образом, подставляя величины напряжений, найденные в результате решения задачи для упругого материала, в условие пластичности, можно установить значение внешней нагрузки, при котором начинается пластическое деформирование материала. При дальнейшем увеличении нагрузки закон Гука, очевидно, уже неприменим и необходимо использовать более общие физические соотношения теории пластичности.

5 Определение остаточных напряжений и деформаций

В заключение рассмотрим вопрос об определении остаточных напряжений и деформаций, сохраняющихся после разгрузки конструкции в силу необратимости пластических деформаций. Предположим, что при некотором значении параметра нагрузки в теле имеют место напряжения 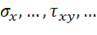и деформации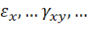

Представим разгрузку как приложение сил, обратных действующим, т. е. соответствующих параметру нагрузки – . Учитывая, что разгрузка осуществляется по закону линейной зависимости, найдем формально напряжения и деформации, возникающие в упругом теле при таком нагружении, т. е.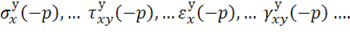

В силу линейности закона разгрузки можно использовать принцип суперпозиции, т. е. получить остаточные напряжения и деформации, сложив исходные величины с образующимися в процессе разгрузки (предполагается, что вторичных пластических деформаций в результате разгрузки не образуется):