Операторы импульса частицы
2. Операторы импульса частицы ![]() ,
, ![]() и
и ![]() выполняют операцию дифференцирования по соответствующей координате:
выполняют операцию дифференцирования по соответствующей координате:
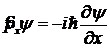 ,
, 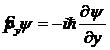 ,
, 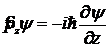 . (12.11)
. (12.11)
3. Операторы момента импульса ![]() частицы выполняют одновременно операции умножения на координаты и дифференцирование по координатам:
частицы выполняют одновременно операции умножения на координаты и дифференцирование по координатам:
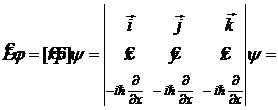
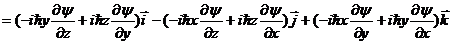 . (12.12)
. (12.12)
4. Оператор потенциальной энергии ![]() выполняет операцию умножения на классическую потенциальную энергию U(x,y,z) частицы
выполняет операцию умножения на классическую потенциальную энергию U(x,y,z) частицы
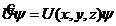 . (12.13)
. (12.13)
5. Оператор кинетической энергии ![]() выполняет операцию дифференцирования по всем координатам
выполняет операцию дифференцирования по всем координатам
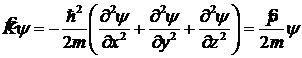 . (12.14)
. (12.14)
Здесь m – масса частицы и
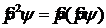
-последовательное двукратное применение оператора импульса ![]() .
.
6. Оператор полной энергии частицы (оператор Гамильтона) ![]() есть сумма операторов кинетической и потенциальной энергий частицы
есть сумма операторов кинетической и потенциальной энергий частицы
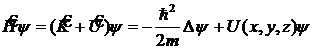 , (12.15)
, (12.15)
где
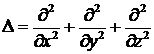
— оператор Лапласа.
Согласно формализму квантовой механики среднее значение измеряемой величины А, которой поставлен в соответствие оператор ![]() , находится с помощью выражения
, находится с помощью выражения
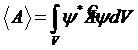 , (12.16)
, (12.16)
где ![]() — волновая функция того состояния частицы, для которого проводится измерение, оператор
— волновая функция того состояния частицы, для которого проводится измерение, оператор ![]() действует только на волновую функцию ψ, стоящую справа от него. Среднее значение квадрата измеряемой величины равно
действует только на волновую функцию ψ, стоящую справа от него. Среднее значение квадрата измеряемой величины равно
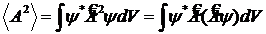 . (12.17)
. (12.17)
Среднеквадратичное отклонение ![]() измеряемой величины описывается известной формулой
измеряемой величины описывается известной формулой
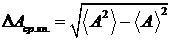 . (12.18)
. (12.18)
Даже в том случае, когда измерения динамической характеристики частицы в точно заданном состоянии осуществляются идеальным прибором без приборной погрешности, среднеквадратичное отклонение может быть отлично от нуля, что связано с квантовым (волновым) движением частицы. Таким образом, законы квантовой механики накладывают фундаментальные ограничения на точность измерения динамических величин, характеризующих движение частиц.
Только в том случае, когда частица находится в состоянии, описываемом собственной функцией ![]() оператора
оператора ![]() , и выполняется соотношение
, и выполняется соотношение
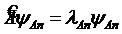 , (12.19)
, (12.19)
где ![]() — вещественное число, называемое собственным значением оператора
— вещественное число, называемое собственным значением оператора ![]() , измеренная величина А имеет нулевую дисперсию:
, измеренная величина А имеет нулевую дисперсию:
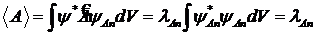 ,
,
и
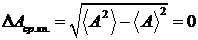 . (12.20)
. (12.20)
Таким образом, в этом случае все измерения динамической величины А идеальным прибором дают для неё одинаковые значения.
При измерении динамических характеристик квантовой системы возникает специфическое взаимодействие между этой микроскопической системой и макроскопическим прибором, которое описывается формальным алгоритмом, называемым редукцией, или коллапсом волновой функции. Согласно данному алгоритму волновая функция ![]() начального состояния системы необратимым образом трансформируется в другую волновую функцию
начального состояния системы необратимым образом трансформируется в другую волновую функцию ![]() , которая и определяет измеренную величину. Эта редукция волновой функции уже не описывается уравнением Шредингера.
, которая и определяет измеренную величину. Эта редукция волновой функции уже не описывается уравнением Шредингера.
Допустим, что измеряется динамическая величина А системы, состояние которой характеризуется волновой функцией ![]() . Для описания результатов измерения волновую функцию необходимо представить в виде разложения
. Для описания результатов измерения волновую функцию необходимо представить в виде разложения
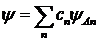 (12.21)
(12.21)
по собственным функциям ![]() оператора
оператора ![]() , соответствующего величине А (см. уравнение (12.19)), где коэффициенты разложения cn удовлетворяют условию нормировки (12.9).
, соответствующего величине А (см. уравнение (12.19)), где коэффициенты разложения cn удовлетворяют условию нормировки (12.9).
Благодаря взаимодействию с макроскопическим измерительным прибором система с вероятностью
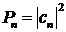 (12.22)
(12.22)
может перейти в состояние, описываемое собственной функцией ![]() , а результат измерения величины окажется равным соответствующему собственному значению
, а результат измерения величины окажется равным соответствующему собственному значению
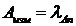 . (12.23)
. (12.23)


