лабораторная работа по электротехнике и электронике
1. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТ. 4
2. ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ОТЧЕТАМ.. 4
ПРИ ВЫПОЛНЕНИИ ЛАБОРАТОРНЫХ РАБОТ. 5
ИССЛЕДОВАНИЕ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПОСТОЯННОГО ТОКА.. 7
ИЗУЧЕНИЕ ВЛИЯНИЯ ПАРАМЕТРОВ НЕРАЗВЕТВЛЕННОЙ ЦЕПИ.. 18
НА АПЛИТУДНО-ФАЗОВЫЕ СООТНОШЕНИЯ.. 18
МЕЖДУ НАПРЯЖЕНИЯМИ ЕЕ УЧАСТКОВ.. 18
РЕЗОНАНС ТОКОВ. ПОВЫШЕНИЕ КОЭФФИЦИЕНТА МОЩНОСТИ ЭЛЕКТРОУСТАНОВОК.. 29
ТРЕХФАЗНАЯ ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ ПРИ СОЕДИНЕНИИ ПРИЕМНИКОВ ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ ЗВЕЗДОЙ.. 39
ЦЕПЬ ТРЕХФАЗНОГО ТОКА С ТОКОПРИЕМНИКАМИ, СОЕДИНЕННЫМИ ТРЕУГОЛЬНИКОМ.. 53
Приложение к лабораторной работе № 1………………………………………..64
Приложение к лабораторным работам № 2 и 3…………………………………67
Приложение к лабораторным работам № 4 и 5……………………………………. 70
1. Лабораторные работы выполняются бригадой из 2-3 студентов согласно установленного графика.
2. Студент допускается к выполнению последующей работы после представления и защиты отчета по предыдущей.
3. Перед началом выполнения лабораторной работы преподаватель устно проводит краткий опрос студентов (допуск к занятию). При неудовлетворительной подготовке к теме занятий студент не допускается к выполнению лабораторной работы.
4. Студенты, пропустившие занятия в лаборатории, допускаются к выполнению пропущенной работы в свободное от занятий время в часы работы лаборатории.
5. При выполнении работы студент обязан:
5.1. При сборке схем сначала собрать последовательные (токовые) цепи, а затем присоединить параллельные цепи (вольтметры, обмотки напряжения ваттметров, счетчиков электроэнергии, цепи управления и сигнализации). Собранная схема обязательно проверяется всеми студентами, выполняющими данную работу, обратив особое внимание на соответствие пределов измерения приборов фактическим электрическим величинам в цепи, на положение рукояток управления, защиты, автоматизации и ползунка реостатов. Они должны находиться в отключенном состоянии, а ползунок реостата в крайнем положении, соответствующем максимальному значению сопротивления;
5.2. Определить цену деления амперметров, вольтметров и ваттметров;
5.3. Получить разрешение от преподавателя на включение собранной схемы в сеть.
5.4. Находиться только на своем рабочем месте, не трогать оборудование и приборы, не относящиеся к работе, соблюдать тишину и порядок;
5.5. По окончании выполнения лабораторной работы представить преподавателю таблицу наблюдений с контрольными расчетами и получить от него подтверждение правильности результатов опытов. В случае неправильности полученных результатов опыт повторить заново.
6. Результаты измерений и наблюдений, полученные в процессе выполнения, обрабатывают в лаборатории и только в отдельных случаях заканчивают дома. По этим данным составляют отчет о выполненной работе в соответствии со всеми пунктами, указанными в методических рекомендациях.
2. ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ОТЧЕТАМ
1. Отчет составляется каждым студентом индивидуально в тетради в клетку.
2. Содержание отчета:
2.1. Номер, название и дата выполнения работы.
2.2. Цель работы.
2.3. Перечень и характеристики (паспортные данные) используемых в работе приборов и оборудования.
2.4. Принципиальные электрические схемы исследуемых цепей.
2.5. Таблицы измеренных и вычисленных величин, основные расчетные формулы и соотношения.
26. Графики зависимостей, потенциальные диаграммы, построенные по таблицам, векторные диаграммы.
2.7. Выводы о результатах проделанной работы, включающие объяснения полученных экспериментальных и расчетных данных.
3. Отчет должен быть написан кратко, аккуратно.
4. Электрические схемы, графики и таблицы выполняются с помощью чертежных инструментов.
5. Электрические схемы выполняются в соответствии с правилами начертания и обозначения элементов согласно ЕСКД.
6. Графики могут быть выполнены на миллиметровой бумаге. Координатные оси должны иметь обозначения изображаемых величин, размерность (единица измерения) и масштаб (шкала, сетка).
7. Отчет представляет каждый студент в отдельности в день выполнения (в отдельных случаях на следующем занятии).
8. При сдаче отчета (защита работы) преподаватель опрашивает студента в объеме материала выполненной работы. В помощь студенту в конце каждой работы приводиться примерный перечень вопросов. Работа зачитывается в том случае, если студент показывает знание цели, физической сущности, методики выполнения работы, использованных аппаратов и оборудования и может объяснить и проанализировать полученные результаты и показать их практическую значимость.
9. Студент, выполнивший все работы и своевременно защитивший их, получает зачет по лабораторной части курса и допускается к сдаче экзамена.
3. ТЕХНИКА БЕЗОПАСНОСТИ
ПРИ ВЫПОЛНЕНИИ ЛАБОРАТОРНЫХ РАБОТ
1. Лабораторные работы проводятся на стенде типа ЛЭС-5, в котором находятся блоки конденсаторов, резисторы с выключателями, 3-х ламповые реостаты, трехфазные маломощные трансформаторы, полупроводниковые диоды, часть которых по мере необходимости используется в той или иной работе. Измерительные приборы применяются в настольном исполнении.
2. Перед началом сборки исследуемой схемы следует убедиться, что питание лабораторного стенда, осуществляемое через автоматический выключатель (автомат), расположенный на левом торце лабораторного стола, отключено.
3. Разрешается подключать собранную схему к напряжению только после проверки ее преподавателем или лаборантом.
4. Перед началом работы переключатели пределов измерения приборов должны быть установлены в положение максимального значения, ручка лабораторного автотрансформатора (ЛАТР) в крайнее положение против часовой стрелки, ползунок реостата — максимальному значению сопротивления, ламповые реостаты должны быть отключены.
5. При включении схемы (медленно поднимая напряжение, при питании через ЛАТР) внимательно следят за показаниями приборов и состоянием исследуемой цепи. Если стрелка какого-нибудь прибора зашкаливает или слышно запах гари, есть потрескивания питание немедленно отключают и о случившемся сообщают преподавателю
6. При включенной схеме запрещается прикасаться к неизолированным токоведущим участкам экспериментальной установки.
7. Запрещается оставлять без присмотра включенное оборудование.
8. По окончании измерений следует отключить напряжение питания стенда, согласовать результаты измерений, разобрать схему экспериментальной установки, навести порядок на рабочем месте.
Лабораторная работа № 1
ИССЛЕДОВАНИЕ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПОСТОЯННОГО ТОКА
Цель работы:
1. Ознакомление с элементами простейшей электрической цепи и с основными величинами, характеризующими работу цепи при различных режимах.
2. Изучение распределения потенциала в неразветвленной электрической цепи.
ПРОГРАММА РАБОТЫ
1. Ознакомиться с оборудованием и приборами лабораторной установки.
2. Собрать электрическую схему (рис. 1.5) и уяснить назначение отдельных ее элементов. Определить цену деления приборов.
3. Выполнить эксперимент по определению основных величин, характеризующих работу цепи в режиме холостого хода и номинальном режиме.
4. Расчетами определить основные величины цепи в режимах согласованной работы и короткого замыкания.
5. Построить по экспериментальным и расчетным точкам совмещенные графики зависимостей U1=U(I), U2=U(I) и Pг=P(I), ΔP=P(I), Рн=Р(I), η= η(I) (см. рис. 1.2 и 1.3).
6. Определить распределение потенциала электрической цепи для указанного преподавателем значения тока.
7. Построить потенциальную диаграмму цепи (см. рис. 1.4).
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
1. Элементы и режимы работы электрической цепи
1.1. Элементы цепи
Основными элементами электрической цепи являются источники и потребители электрической энергии, линии электропередач (ЛЭП) или соединительные провода.
В качестве источников постоянного тока широкое распространение получили генераторы постоянного тока, гальванические элементы и выпрямительные блоки питания, характеризующиеся электродвижущей силой (ЭДС) Е и внутренним сопротивлением Rо.
Потребителями электрической энергии являются нагреватели, электрические двигатели, электрические лампы и т. д., в которых электрическая энергия преобразуется соответственно в тепловую, механическую, световую и другие виды полезной энергии.
Все остальные элементы электрической цепи: электроизмерительные приборы, коммутационная аппаратура и т. д. являются вспомогательными. Любая электрическая цепь характеризуется током, электродвижущей силой и напряжением.
Рассмотрим простейшую электрическую цепь (рис. 1.1) с источником электрической энергии (ИЭ) и потребителем (П) линией электропередач (ЛЭП).
Предположим, что в источнике ИЭ преобразуется какой-то вид энергии в электрическую. Это происходит за счет так называемых сторонних (не электрических: механических, химических, тепловых, световых и т. д.) сил, которые производят внутри источника разделение зарядов, создавая ЭДС. Величина, численно равная работе W, совершаемой сторонними силами (механические, химические и др.) при перемещении единицы заряда q внутри источника, называется ЭДС,
Е=W / q.
Единицей измерения ЭДС является вольт (В).[Е]=Дж/Кл=В.
Если цепь замкнуть (ключом S), то разделенные заряды под воздействием электрического поля стремятся объединиться. Вследствие движения зарядов в цепи возникает ток I, и в потребителе П сопротивлением нагрузки Rн преобразовывается энергия, запасенная источником, в какой-то другой вид полезной энергии (тепловую,
световую, механическую и т. д.). В то же самое время внутреннее сопротивление источника Rо, и сопротивление линии электропередач 2Rлбудут нагреваться этим током, что приводит к бесполезной затрате энергии источника.
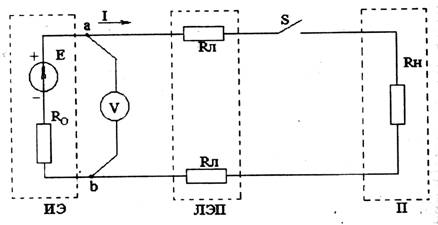
Рис. 1.1
Вдоль пути вне источника (на пассивном участке цепи), где нет сторонних сил, величина, численно равная работе, которую совершает источник по переносу единицы заряда по данному участку цепи, называется напряжением U. Единица напряжения та же, что и ЭДС
[U] = Дж/Кл = В.
Из определений очевидно, что ЭДС источника равна сумме напряжений на внешнем и внутреннем участках цепи
E=Uвш+Uвн,
где Uвш – напряжение на нагрузке Rн и ЛЭП 2Rл (на внешнем участке цепи);
Uвн – напряжение на внутреннем сопротивлении Rо источника (на внутреннем участке цепи).
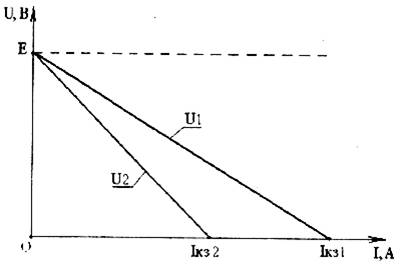
Рис. 1.2
Эта формула выражает закон сохранения энергии для электрических цепей. Измерить напряжение на различных участках цепи можно только при замкнутой цепи. ЭДС измеряют между зажимами источника при разомкнутой цепи.
Напряжение на пассивном участке цепи часто называют еще падением напряжения.
Электрическое напряжение вдоль пути вне источника между точками а и вназывают также разностью потенциалов между этими точками
Uab = Ua-Ub.
Чтобы определить разность потенциалов, необходимо потенциал одной из точек приравнять к нулю, тогда потенциал другой точки будет равен падению напряжения между этими точками.
Для количественной оценки электрического тока служит величина называемая силой тока (или просто током), равная величине заряда в 1 кулон (Кл), прошедшей через данноесечение проводника за единицу времени t(c),
I =q / t.
Единицейсилы тока является ампер (А), [I] = Кл/с = А.
Ток в цепи (рис. 1.1) по закону Ома
I=E/(Ro+2Rл+Rн)=E/(R∑ +Rн) (1.1)
где Ro — внутреннее сопротивление источника электроэнергии;
2Rл — сопротивление линии электропередач;
RΣ=Rо+2Rл — суммарное сопротивление источника и ЛЭП;
Rн — сопротивление нагрузки.
Из соотношения (1.1) имеем
E=I(R∑ +Rн )=Uвн+Uл+Uн, (1.2)
где Uвн — падение (потеря) напряжения на источнике электроэнергии, Uвн=RoI.
Uн — падение напряжения на нагрузке (преобразование в полезную работу), Uн=IRн;
Uл — падение (потеря) напряжения на ЛЭП, Uл=2RлI.
Мощность Рн, потребляемая нагрузкой, называется полезной мощностью электрической энергии и она равна
Рн=I2Rн. (1.3)
Другая часть мощности источника электрической энергии, затрачиваемая на пути движения тока к нагрузке (в источнике и ЛЭП), называется мощностью потерь и равна
ΔР = I2(Ro + 2Rл) = I2RΣ . (1.4)
Баланс мощностей для электрической цепи
Рг=Рн+ΔР=I2Rн+I2RΣ, (1.5)
где Рг — мощность, вырабатываемая источником электрической энергии
Рг = ЕI. (1.6)
Коэффициент полезного действия электрической цепи есть отношение полезной мощности Рнк мощности, вырабатываемой источником Рг, и равен
h=(Рн/Рг)*100%=((Рг-DР)/Рг)*100%=
=((1-DР)/Рг)*100%=((1-I2RΣ)/ EI)*100%(1.7)
1.2. Режимы работы электрической цепи
Электрическая цепь (рис. 1.1 и 1.5) в зависимости от значения сопротивления нагрузки может работать в следующих режимах:
— режиме холостого хода (РХХ);
— номинальном режиме (HP);
— режиме согласованной нагрузки (РСН);
— режиме короткого замыкания (РКЗ).
1.2.1. Режим холостого хода
В режиме холостого хода внешняя цепь разомкнута (выключатель S2отключен) и ток I=Iхх=0. Так как реальный источник электрической энергии имеет внутреннее сопротивление Rо, которое на схеме обычно показывается в виде отдельного элемента, то при отсутствии тока в цепи нет падения напряжения на внутреннем сопротивлении. В этом случае вольтметр V1, подключенный к выводам источника (точка а и в), покажет численное значение ЭДС Е источника, т. е.
U = Uxx = Е.
1.2.2. Номинальный режим
Для получения максимального коэффициента полезного действия η электрической цепи элементы цепи должны работать в условиях, соответствующих проектным данным и параметрам, т. е. в номинальном режиме. Номинальные значения тока, напряжения, мощности и КПД указываются в паспортах изделий
Iном, Uном, Рном, ηн
1.2.3. Режим согласованной нагрузки
В этом режиме работы электрической цепи сопротивление нагрузки Rнравно суммарному сопротивлению RΣ (источника электроэнергии Rо и линии электропередач 2Rл).
Покажем, что мощность приемника будет максимальной, если Rн=RΣ=Ro+2Rл.
Мощность приемника (нагрузки)
Рн=RнI2=Rн(Е/(RΣ+Rн))2 (1.8)
Приравняв к нулю первую производную мощности по сопротивлению нагрузки, найдем условие, когда мощность приемника будет максимальной
dРн/dRн= 0,
откуда Rн = RΣ.
Нетрудно установить, что в режиме согласованной нагрузки (когда Rн=RΣ) из равенств (1.2 и 1.8)
Uн = 0,5 Е; Рн=Е2 / 4Rн.
При этом η=Rн / (RΣ +Rн)= 0,5, т. е. имеет невысокое значение.
Из-за низкого КПД согласованный режим применяется, главным образом, в маломощных цепях (например, в устройствах радиоэлектроники, в автоматике и измерительной технике), когда КПД не имеет существенного значения, а требуется лишь получить максимально возможную мощность в приемнике. Этот режим является для них номинальным.
В цепях же большой мощности Ro<<Rн и КПД близок к единице. Поэтому для мощных цепей работа в согласованном режиме экономически не выгодна.
1.2.4. Режим короткого замыкания
Режим короткого замыкания возникает тогда, когда выводы источника или приемника по каким-либо причинам накоротко соединены между собой. В случае замыкания выводов приемника напряжение на приемнике Uн=0, а сопротивление всей цепи равно 2Rл+Rо. Тогда ток в цепи (ток короткого замыкания) будет равен
Iкз2=Е / (2Rл +R0).
В случае замыкания выводов источника сопротивления ЛЭП исключаются из сопротивлений цепи, и ток короткого замыкания будет равен
Iкз1=Е / R0.
Это значение тока будет максимально возможным для данного источника, и вся энергия источника целиком преобразуется в тепло в своем сопротивлении Ro, что может вызвать перегрев источника и даже повреждение.
Для защиты источников электрической энергии от тока короткого замыкания устанавливают:
— в маломощных цепях — плавкие предохранители;
— в более мощных — плавкие предохранители или автоматические выключатели с электромагнитными расцепителями;
— в высоковольтных цепях — специальные высоковольтные выключатели.
Из особенностей работы электрической цепи в рассмотренных выше режимах следует, что зависимость напряжения U1 на клеммах источника энергии имеет вид
U1 = U1(I) = E-IRо (1.9)
и представляет собой в координатах U-I прямую линию, пересекающую ось U при РХХ (I =0, U1=Е) и ось I при РКЗ (I =Iкз1; U1 =0) (рис.1.2). Здесь Iкз1 = Е/Rо — ток короткого замыкания на клеммах источника (между точками а и в, рис. 1.5).
Функция U2=U2(I) на нагрузке RH определяется выражением
U2 = U2(I) = Е — I RΣ (1.10)
и представляет собой прямую линию, пересекающую ось U при РХХ (I=0; U2=E) и ось I при РКЗ (I=Iкз2; U2=0) (рис. 1.2). Здесь Iкз2=E/RΣ – ток короткого замыкания на клеммах нагрузки (между точками с и d, рис. 1.5).
Зависимость ΔP=P(I)=I2RΣпредставляет собой параболу, проходящую через начало координат при РХХ /I=0; ΔР=0/ и имеющей максимум при РКЗ /I=Iкз2;Р=Iкз2Е/ (рис. 1.3). В последнем случае вся энергия расходуется только на нагрев источника и ЛЭП.
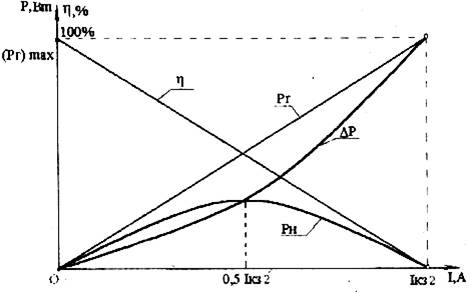
Рис. 1.3
Мощность, потребляемая нагрузкой,
Pн=Pн(I) = I2Rн=EI — I2RΣ
изменяется нелинейно, пересекая ось I при РХХ (I =0; Рн=0) и при РКЗ (I=Iкз2, Рн=0) (рис. 1.3). Максимум мощности имеет место при РСН (I=Е/2RΣ;
Рн=Е2 / 4RΣ), когда Rн=R∑. В режиме согласованной нагрузки Рн=DР.
КПД электрической цепи для любого режима работы
h=(1-(IRΣ/E))*100%
представляет собой прямую, проходящую через координаты: при PXX(I=0; h=100%) и при Pкз(Iкз2=Е / RΣ;h=0) (см. рис. 1.3).
2. Распределение потенциала в неразветвленной электрической цепи
При анализе электрических цепей часто необходимо знать разность потенциалов между отдельными точками и распределение потенциала в цепи. Для этого строится потенциальная диаграмма — график зависимости U(R), построенный при обходе контура против направления тока (рис. 1.4).
В идеальном источнике ЭДС потенциал изменяется скачком, поэтому источнику ЭДС соответствует вертикальный участок потенциальной диаграммы (прямая an). Линия nb — падение напряжения на внутреннем сопротивлении источника. Напряжение на выводах источника (Uab) показывается наклонной линией (штриховая линия аb).
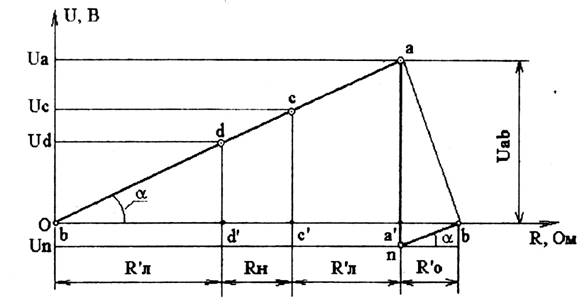
Рис 1.4
По закону Ома падение напряжения на сопротивлении Rл составит Udb=IRл=Ud-Ub или, если принять потенциал точки b равным нулю, то Ub=0иUd=RлI>Ub (ток в сопротивлении протекает от точки с большим потенциалом к точке с меньшим потенциалом). Падение напряжения на сопротивлении Rн равно Ucd=IRн=Uc-Ud, откудаUc=Ud+IRн. Аналогично:
Uac=IRл=Ua-Uc, откуда Uа=IRл+ Uc;
Una=-E=Un-Ua, откуда Un=Ua-E;
Ubn=IPo=Ub-Un, откуда Ub=Un+IRo.
На участках с сопротивлениями Ro, Rн, Rл (рис. 1.4) имеет место постепенное изменение потенциала, причем угол наклона, характеризующий эти изменения, везде одинаков, так как в неразветвленной цепи ток один и тот же, и
tgα=(Mu/MR)*(U/R)=(Mu/MR)*I=const,
где Mu, Mr — масштабы соответствующих величин.
СХЕМА УСТАНОВКИ
Схема установки представлена на рис. 1.5.
Она включает в себя:
1 — источник постоянного тока с выпрямительным блоком питания, который может обеспечить ступенчатое регулирование выпрямленного напряжения до 75 В при номинальном токе в цепи Iн = 4 А;
2 — ЛЭП — физическая модель линии электропередач, состоящая из двух проводников Rл высокого сопротивления (нихром);
3 — нагрузка, представляющая собой регулируемый реостат на 10 Ом, спаренный из двух половин, последовательно включенных между собой;
SI, S2 — выключатели;
SF — автомат стенда;
А — амперметр на 5 А;
VI, V2 — вольтметры на 75 В.

Рис 1.5
МЕТОДИКА И ПОСЛЕДОВАТЕЛЬНОСТЬ ВЫПОЛНЕНИЯРАБОТЫ
1. Собрать электрическую цепь согласно рис. 1.5. Установить сопротивление нагрузки Rн на максимальную величину. После проверки схемы преподавателем, при выключенных автомате стенда SFи ключей S1иS2, запитать шнур блока питания от розетки.
2. Включить автомат SFстенда и ключ S1.
При отключенном выключателе S2 вольтметром VI измерить ЭДС Е источника электрической энергии. Обратить внимание на одинаковые показания вольтметров VI и V2, равные величине ЭДС источника.
4. Замкнуть ключ S2, и реостатом Rн последовательно устанавливать по амперметру А значения тока в цепи I=1 А; 2 А;3 А; 4 А. При этом производить замер напряжений вольтметрами V1и V2, отмечая неодинаковые изменения их показаний по мере роста тока I. Результаты замеров занести в табл. 1.1.
Таблица 1.1
|
№ п/п |
Измерено |
Вычислено |
||||||||
|
E |
U1 |
U2 |
I |
R0 |
R∑=R0+2Rл |
Рг |
DР |
Рн |
h |
|
|
В |
А |
Ом |
Вт |
% |
||||||
|
1 |
||||||||||
|
2 |
||||||||||
|
3 |
||||||||||
|
4 |
||||||||||
|
5 |
||||||||||
|
Среднеарифметические значения сопротивлений |
R0= |
R∑= |
— |
— |
— |
— |
||||
|
6 |
I6=Iкз2=E/R∑= |
|||||||||
|
7 |
I7=Iкз2/2= |
|||||||||
|
8 |
I8=Iкз1=E/R0= |
5. Последовательность измерений для построения потенциальной диаграммы.
5.1.В схеме рис. 1.5. включить автомат SFстенда и ключ S1, при отключенном выключателе S2 замерить Е источника электрической энергии (аналогично п. п.2. и 3.).
5.2.При включенном ключе S2 для одного значения тока (по указанию преподавателя) с помощью универсального переносного вольтметра измерить напряжения указанных точек (а, с, d, п)относительно точки в, потенциал которой принимаем равным нулю.
Данные измерений заносим в табл. 1.2.
Таблица 1.2
|
Измерено |
Вычислено |
||||||||||||
|
I |
E |
Udb |
U2=Ucd |
Ucb |
U1=Uab |
Unb |
Rн |
||||||
|
Дел |
А |
дел |
В |
дел |
В |
дел |
В |
дел |
В |
дел |
В |
В |
Ом |
ОБРАБОТКА ОПЫТНЫХ ДАННЫХ
1. Величины R0 и R0+2Rл в табл. 1.1 для каждого замера находят по формулам
R0=(E-U1)/ I
R0+2 Rл= (E-U2)/ I
2. По полученным результатам R0 и R∑=R0+2Rлопределяютих среднеарифметические значения R0 и R∑.
3. Рассчитывают токи для остальных режимов (п. 6-9) (табл. 1.1) по формулам
I6=Iкз2=Е/R∑, I7=Iкз2/2, I8=Iкз1=Е/R0,
4. Для измеренных и рассчитанных значений токов определяют остальные электрические параметры цепи (табл. 1.1).
5. По экспериментальным и расчетным точкам строят совмещенные графики:
5.1 .напряжений U1(I) и U2(I) (см. рис. 1.2);
5.2.мощностей Рг(I), ΔР(I), Рн(I) и h(I) (см. рис. 1.3).
6. По полученным графикам проводят анализ работы электрической цепи.
7. По полученным результатам табл. 1.2 рассчитывают неизвестные величины
Unb=I Ro; Rн=U2/I.
Значения RoиRлберутся из табл. 1.1(Rл= (R∑-R0) / 2).
8. Строят потенциальную диаграмму электрической цепи всистеме координат U-R. По оси абсцисс откладывают отрезки, соответствующие (в выбранном масштабе) сопротивлениям участков цепи:
bd’ = R’л;d’c’ = Rн; с’а’ = Rл и a’b = R’0.
9. По оси ординат откладывают найденные величины ЭДС и напряжений, приняв потенциал точки bравным нулю(Ub=0).
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. До начала занятий
1.1. Охарактеризуйте типовые режимы работы электрической цепи.
1.2. Напишите формулу закона Ома для замкнутой цепи, для участков цепи, указанных преподавателем.
1.3. Чем отличается ЭДС источника от напряжения? Как измерить ЭДС?
1.4. Что такое падение напряжения, потеря напряжения? Чем они отличаются друг от друга?
1.5. Что такое потенциал точки? Разность потенциалов точек?
2. После выполнения работы
2.1. Укажите на графиках точки, соответствующие типовым режимам работы электрической цепи. Выделите среди них согласованный режим.
2.2. Объясните характер изменения графиков напряжений U1(I), U2(I).
2.3. Проанализируйте закономерность изменения мощностей электрической цепи.
2.4. Объясните смысл КПД и характер его изменения с ростом тока.
2.5. Проанализируйте полученную потенциальную диаграмму и рассчитайте потенциал точки, указанный преподавателем.
2.6. Объясните назначение потенциальной диаграммы.
Лабораторная работа № 2
ИЗУЧЕНИЕ ВЛИЯНИЯ ПАРАМЕТРОВ НЕРАЗВЕТВЛЕННОЙ ЦЕПИ
НА АПЛИТУДНО-ФАЗОВЫЕ СООТНОШЕНИЯ
МЕЖДУ НАПРЯЖЕНИЯМИ ЕЕ УЧАСТКОВ
Цель работы:
1. Установить влияние параметров цепи на амплитудные и фазовые значения напряжений на участках.
2. Ознакомиться с явлением резонанса напряжений.
ПРОГРАММА РАБОТЫ
1. Ознакомиться с оборудованием и приборами лабораторной установки ЛЭС-5.
2. Собрать электрическую схему (рис. 2.7.) и уяснить назначение отдельных ее элементов. Определить цену деления приборов.
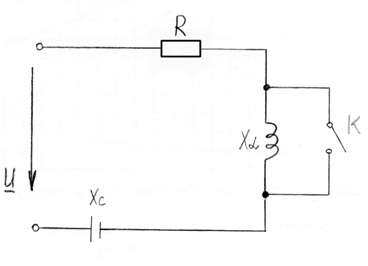
3. Выполнить эксперимент по определению влияния параметров неразветвленной цепи на амплитудно-фазовые соотношения между напряжениями ее участков и тока цепи. Рассмотреть три характерных случая: преобладание индуктивного (Xl>Xc), емкостного (Xl<Xc) сопротивлений и резонанс напряжений (Xl=Xc).
4. Для каждого характерного случая (по указанию преподавателя) по результатам измерений построить векторные диаграммы (рис. 2.2 — 2.4). По полученным данным построить в одной системе координат совмещенные графики двух групп функций:
рис.2.5.: Z=Z(LK); XL=X(LK); X=X(LK); R=R(LK); XC=X(LK) и
рис.2.6.: Z=Z(XL); I=I(Xl); UL=U(Xl); Uc= U (Xl); cosj = cosj (Xl).
5. При полностью вставленном сердечнике в катушку, постепенно уменьшая емкость конденсаторной батареи, убедиться в возможности достижения резонанса напряжений изменением только емкости цепи.
ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ
При анализе цепей синусоидального тока, в отличие от цепей постоянного тока, необходимо учитывать не один, а три пассивных элемента: резистивный, индуктивный и емкостный. Они характеризуются соответственно активным сопротивлением R(в комплексном виде R),индуктивным сопротивлением Xl=wL(в комплексном виде XL=jwL) и емкостным сопротивлениями Хс=1/wC) (в комплексном виде Хс=-j1/wC),
гдеw — угловая частота тока, равная 2pf, рад/с,
f — линейная частота тока, f=50 Гц.
Резистор является необратимым преобразователем электромагнитной энергии в полезные виды энергии (лучистую, тепловую, механическую, звуковую и т. д.), конденсатор накапливает энергию электрического поля, а катушка индуктивности — энергию магнитного поля.
Индуктивность катушки определяет ее способность создавать магнитное поле при прохождении через нее тока:
L=Фw/I, Гн, (2.1)
где Ф — магнитный поток одного витка, Вб;
w — число витков катушки;
I — ток, А.
Индуктивность катушки зависит от числа ее витков и магнитного сопротивления магнитопровода Rm, на который она намотана:
L=w2/(Rm), (2.2)
где Rm=1/(mm0S) — магнитное сопротивление, 1/Гн;
1 — средняя длина магнитопровода, м;
S — площадь его сечения, м2;
m — относительная магнитная проницаемость материала сердечника, показывающая во сколько раз магнитное поле в сердечнике больше, чем в вакууме (для электротехнической стали m>500);
mо — абсолютная магнитная проницаемость вакуума или магнитная постоянная, равная 4p10-7 Гн/м.
Из выражения индуктивности (2.2) видно, что ее можно регулировать при постоянном числе витков магнитным сопротивлением, изменяя положение сердечника относительно катушки.
В свою очередь емкость конденсатора определяется его конфигурацией и относительной диэлектрической проницаемостью диэлектрика, помещенного между его пластинами. Для плоского конденсатора
C=(ee0S)/l, Ф, (2.3)
где S — площадь одной пластины, м2;
l — расстояние между пластинами, м;
e0= 1/(4p·9·109) — абсолютная диэлектрическая проницаемость вакуума или электрическая постоянная, Ф/м;
e — относительная диэлектрическая проницаемость.
ИндуктивноеXL и емкостное Хс сопротивления определяют не только значения токов и напряжений в цепи, но также сдвиг фаз между напряжениями и токами.
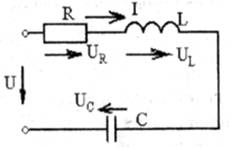
Рис. 2.1
При последовательном соединении R, L, С элементов (рис.2.1) под действием синусоидального напряжения u=Umsin(wt+yu) (в комплексной форме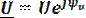 ) через все элементы цепи течет один и тот же синусоидальный ток i=Imsin(wt+yi) (в комплексной форме
) через все элементы цепи течет один и тот же синусоидальный ток i=Imsin(wt+yi) (в комплексной форме 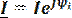 ),
),
где Um, Im — амплитудные значения напряжения и тока;
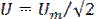 ,
, 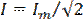 действующие значения напряжения и тока, регистрируемые соответственно вольтметром V1 и амперметром А (рис.2.7).
действующие значения напряжения и тока, регистрируемые соответственно вольтметром V1 и амперметром А (рис.2.7).
Необходимо иметь ввиду, что активное сопротивление R, показанное на схеме (рис.2.1) отдельно, может быть как сопротивлением специально включенного резистора, так и сопротивлением проводов реальной катушки (рис.2.7), последнее из которых и имеет место в этой работе.
На каждом элементе будет падать напряжение UR, UL, Uc, которые в комплексной форме запишутся
UR=IR, UL =jXLI, Uc =.-jXcI (2.4)
По второму закону Кирхгофа получим
U=UR+UL +Uc =U2+U3 =U1 (2.5)
где U2=UR+UL= IR+ jXLI — падение напряжения нареальной катушке индуктивности;
(2.6)
U3=UС= — jXСI-. (2.7)
падение напряжения на конденсаторе
Поэтому
U=UR+UL +Uc =U2+U3 =RI+jI(XL-Xc), (2.8)
тогда закон Ома для цепи переменного тока в комплексной форме:
I=U / [R+j(XL-Xc)]=U / Z, (2.9)
где Z=R+j(Xl-Xc)=R+JX — комплексное сопротивление цепи;
X=XL-Xc — реактивное сопротивление цепи.
Комплексное сопротивление в показательной форме:
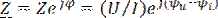 , (2.10)
, (2.10)
где
Z=U/I (2.11)
![]()
(полное сопротивление цепи); (2.12)
j=arctg(XL-Xc)/R аргумент комплексного сопротивления; (2.13)
j=yu-yi — угол сдвига фаз между напряжением и током. (2.14)
Из приведенных формул (2.9-2.14) можно сделать следующие выводы:
а) действующее значение тока в цепи Iс последовательно включенными элементами R, L и С пропорционально действующему значению приложенного напряжения U и обратно пропорционально полному сопротивлению цепи Z(2.11), т. е. I=U/Z;
б) угол сдвига фаз jмежду напряжением и током равен аргументу комплексного сопротивления (2.13);
в) знак угла сдвига фаз определяется знаком реактивного сопротивления X=XL-Xс. Если XL>Хс (для этой работы сердечник полностью вставлен в катушку и тем самым индуктивность L наибольшая) и UL>Uc, то цепь имеет активно-индуктивный характер, т. е. I по фазе отстает от напряжения U на угол 0<j< 90° (рис. 2.2 при yi=0);
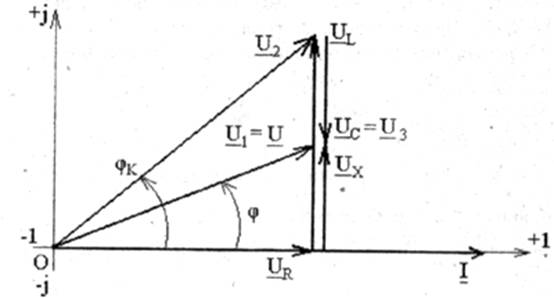
Рис. 2.2
г) если XL<Xc (сердечник полностью удален из катушки, а емкость конденсатора осталась без изменения) UL<Uc, то цепь имеет активно-емкостный характер, т. е. ток I по фазе опережает напряжение U на угол 0>j>-90° (рис. 2.3);
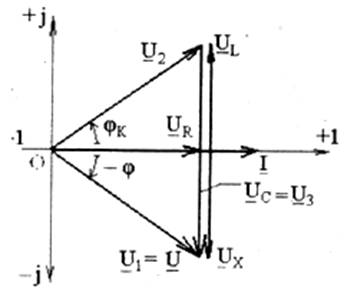
Рис. 2.3
д) когда XL=Xc (сердечник удален только частично) и UL = Uc, а j=0 наступает резонанс напряжений (рис.2.4).Этот режим имеет место, исходя из XL=wL и Хс=1/wC, угловая частота при этом равна
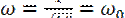 , (2.15)
, (2.15)
где w0 — резонансная (собственная) частота цепи.
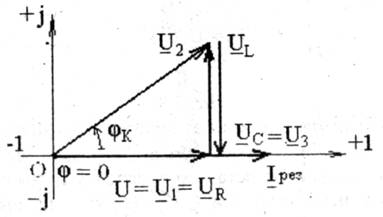
Рис. 2.4
Электрические цепи лучше всего "отзываются" на настройку в резонансе с электромагнитным колебанием с угловой частотой w0 за счет изменения частоты цепи, чем L и С. На использовании резонанса основана настройка приемных и передающих устройств на определенную частоту в технике связи и автоматике. В частности, при настройке приемника на частоту радиостанции изменяют конденсатор переменной емкости до тех пор, пока контур приемника, состоящий из L и С, не настроится в резонанс на частоту, с которой работает искомая радиостанция.
Резонансу напряжений сопутствуют ряд характерных особенностей, которые обусловили его широкое применение в радиотехнике, электротехнике, измерительной технике, автоматике и других областях. Они следующие:
1. Так как j=0, то cosj=1 (рис. 2.6). Полное сопротивление цепи количественно минимально и качественно равно активному (см. рис. 2.5)
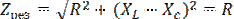 (2.16)
(2.16)
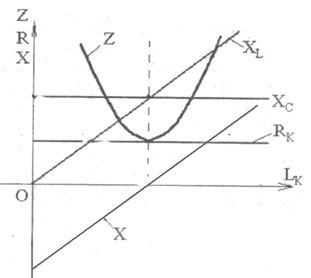
Рис 2.5
2.Ток Iрез=U/Zрез=U/R— максимален (рис. 2.6). Это свойствопозволяет обнаружить резонанс напряжений при изменении w, L или С. Однако резонансный ток при определенных условиях опасен, так как может привести к перегреву элементов цепи и выходу их из строя.
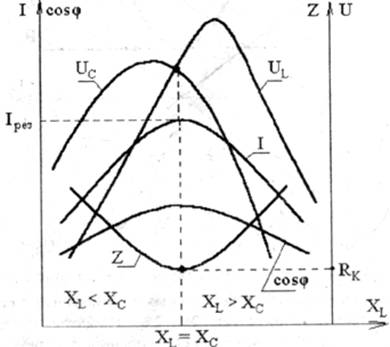
Рис.2.6
3. Напряжения на отдельных участках контура:
UR= RIрез = U, UL = ХLIрез, Uc= ХСIрез. (2.17)
Если XL= Хс>R, то UL= Uc>UR=U (причем 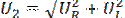 несколько больше U3, см. рис.2.7), т. е. напряжение на участках с реактивными элементами больше, чем напряжение источника (рис.2.4, 2.6). Свойство усиления напряжения является важнейшей особенностью резонанса напряжений и широко используется в технике. Коэффициент усиления напряжения ku равен добротности последовательного контура Q. Он характеризует собой отношение реактивной энергии I2pesXLt, накопленной в контуре в магнитном и электрическом полях, к активной (тепловой) энергии I2pesRt, расходуемой в активном сопротивлении R:
несколько больше U3, см. рис.2.7), т. е. напряжение на участках с реактивными элементами больше, чем напряжение источника (рис.2.4, 2.6). Свойство усиления напряжения является важнейшей особенностью резонанса напряжений и широко используется в технике. Коэффициент усиления напряжения ku равен добротности последовательного контура Q. Он характеризует собой отношение реактивной энергии I2pesXLt, накопленной в контуре в магнитном и электрическом полях, к активной (тепловой) энергии I2pesRt, расходуемой в активном сопротивлении R:
ku= UL/(U=UR)=(ХLIрез)/(RIрез)=(ХLI2резt)/(RI2резt)=XL / R = r/R=Q, (2.18)
где ρ=ХL=w0L= 1/(w0C) — характеристическое сопротивление последовательного контура.
Резонанс напряжений в электросистемах иногда возникает непредвиденно и приводит к тому, что на отдельных участках возникают перенапряжения, в несколько раз превышающие рабочие напряжения.
Такое значительное повышение напряжения на реактивных элементах при резонансе может привести к пробою изоляции и опасно для обслуживающего персонала. Это обстоятельство должно быть учтено при проектировании и эксплуатации электротехнических устройств с подобными контурами.
4. Активная мощность при резонансе максимальна, так как ток Iрез максимален, т. е. Р=RI2рез. Реактивные мощности равны, так как ХLI2рез=ХсI2рез, но мгновенные значения их противоположны по знаку. Это означает происходящий обмен реактивных энергий между магнитным полем индуктивности и электрическим полем емкости цепи, в котором источник питания не участвует, что является весьма важным свойством контуров.
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
Схема экспериментальной установки представлена на рис. 2.7,
где ЛАТР — лабораторный автотрансформатор
Rk, LK — активное сопротивление проводов и индуктивность реальной катушки
ZK — полное сопротивление катушки
C1 и С2 — конденсаторы соответственно на 30мкФи0…34, 75 мкФ.
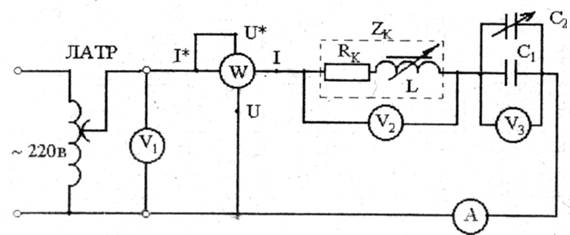
Рис. 2.7
Для проведении лабораторной работы на установке необходимы:
1.Лабораторный автотрансформатор ЛАТР (U=0…250 В иI=0..2 А) -1шт;
2. Вольтметр V1=(0…75 В) — 1шт;
3. Ваттметр W (I=2,5…5 A, U=150В) — 1 шт,
4. Катушка индуктивности с подвижным сердечником(W=1200 витков) — 1 шт;
5. Батарея конденсаторов (C1=30 мкф и С2=0…34,75 мкф) С=58 мкф — 1 шт;
6. Вольтметр V2 и V3 (0…150 В) — 2 шт;
7. Амперметр А (0… 1 А) — 1 шт.
Таблица 2.1
|
№ |
Измерено |
Вычислено |
Вид нагрузки |
|||||||||||||||
|
I |
P |
U1 |
U2 |
U3=Uc |
Z |
R |
X |
Xc |
XL |
Lk |
cosj |
j |
jk |
Ur |
UL |
|
||
|
А |
Вт |
В |
Ом |
Гн |
о. е. |
град |
град |
|
||||||||||
|
1 |
XL>Хс |
|
||||||||||||||||
|
2 |
|
|||||||||||||||||
|
3 |
XL= Хс |
|
||||||||||||||||
|
4 |
XL<Хс |
|
||||||||||||||||
|
5 |
|
ПОРЯДОК ПРОВЕДЕНИЯ ОПЫТОВ
1. Собирают электрическую цепь согласно рис. 2.7. Рукоятку ползунка ЛАТРа устанавливают на нулевое положение, мягко доведя против часовой стрелки до упора. Сердечник вставляют в катушку, переключатели измерительных приборов переводят на следующие положения: вольтметр V1 на 75 В, амперметр А на 1 А, катушка напряжения ваттметра на 75 В, катушка токовая на 2,5 А, вольтметры V2и V3на 150 В. С разрешения преподавателя включают питание и медленным поворотом по часовой стрелке ручки ЛАТРа, следя за показаниями приборов, устанавливают напряжение цепи U1=30…35 В и во время опыта поддерживают его постоянным.
2. Плавно выдвигая сердечник из катушки индуктивности до полного его удаления, убеждаются по показаниям амперметра А и ваттметра W в том, что ток цепи и потребляемая активная мощность сначала увеличиваются (Xl>Xc), достигая своего максимума (XL= Хс), а затем уменьшаются (XL<Хс).
3. Вставляют сердечник в катушку. Перемещая его как в п.2 производят измерения при пяти различных положениях сердечника.
4. Два измерения производят при нарастании тока, начиная с положения сердечника, когда он полностью вставлен в катушку.
5. Третье измерение при резонансе производят при максимальных токе и мощности. Причем показание вольтметра V2 при этом должно быть несколько больше, чем показание вольтметра V3.
6. Последующие два измерения проводят при убывании тока. Пятое измерение выполняют для полностью удаленного сердечника. Результаты измерений и расчетов заносят в табл. 2.1.
7. Полностью вставляют сердечник в катушку индуктивности. Постепенно уменьшают емкость конденсаторной батареи С, наблюдая за показаниями приборов, убеждаются что и при изменении только емкости также достигается резонанс напряжений.
ОБРАБОТКА ОПЫТНЫХ ДАННЫХ
1. Расчетные параметры определяются из следующих соотношений:
1.1.Полное сопротивление цепи Z=U1/I, Ом.
1.2.Активное сопротивление проводов катушки R=P/I2, Ом.
1.3.Емкостное сопротивление конденсатора Xc=Uc/I, Ом или Xc=1/(2pfC).
1.4.Реактивное сопротивление цепи
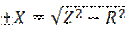 ,Ом.
,Ом.
При XL>XC (п. l, 2) X>0, если XL<Xc (п.4, 5) X<0.
1.5.Индуктивное сопротивление катушки Xl=±X+Xc, Om.
1.6.Индуктивность катушки
Lk=XL/(2pf), Гн,
где f=50 Гц.
1.7.Коэффициент мощности цепи cosj =P/S=P/(U1*I).
1.8. Угол сдвига по фазе напряжение катушки относительно тока
jк=arc tg (Xl/R)
1.9. Падение напряжения на активном и индуктивном сопротивлениях катушки
UR=IR и UL=IXL.
2. Векторные диаграммы строят для грех характерных случаев (п.1 или 2, п. 3, п.4 или 5 по указанию преподавателя) следующим образом.
Предварительно выбирают масштабы напряжений МU (В/см), тока M1 (А/см), проводят оси комплексной плоскости. За основной вектор (опорный) для последовательной цепи принимают вектор тока, так как значение тока на всех участках цепи одинаково. Ток располагают по вещественной оси (+1), принимая для удобства начальную фазу тока yi=0.Построение векторной диаграммы проводят на основании равенства U1=U2+U3.
Напряжение катушки U2 строят через его составляющие — активную UR, отложив ее вдоль тока, и индуктивную UL, отложив ее перпендикулярно току, согласно равенству U2 = UR+UL, где UR=IR, UL=IXL
К концу вектора U2, пристроив напряжение конденсатора под углом 90° относительно тока Iв направлении движения часовой стрелки, т. е. в противофазе с UL, получают общее напряжение U1. Напряжение U1 в соответствии с равенством U1 = UR-UX раскладывают на составляющие, где UX = UL-UC.
3. В общей системе координат Z=Z(LK) строят по данным табл. 2.1 совмещенные кривые изменения полного Z, индуктивного XL, емкостного Хс, реактивного X и активного R сопротивлений от индуктивности катушки Lk (рис. 2.5).
4. В функции от индуктивного сопротивления Xlстроят совмещенные графики полного сопротивления Z, тока цепи I, коэффициента мощности цепи cosj, емкостного Uc и индуктивного Ulпадений напряжений (рис.2.6).
5. По векторным диаграммам и указанным выше графикам функций проводят анализ работы неразветвленной цепи. По приведенным ниже вопросам дают ответы до выполнения (допуск к выполнению работы) и после выполнения лабораторной работы (защита).
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Перед выполнением работы
1.1.Какое явление называется резонансом напряжений? Каково условие наступления резонанса? По какому признаку определяют наличие резонанса?
1.2.Объясните сущность изменения индуктивности катушки от положения вставленного сердечника.
1.3.Какой вид имеет закон Ома для неразветвленной цепи?
1.4.Какие сопротивления имеют место в цепях переменного тока? Их физический смысл?
1.5.Как по показаниям приборов установить, какой именно характер нагрузки в цепи?
1.6.Почему напряжение на реальной катушке индуктивности при резонансе больше напряжения конденсатора?
1.7. Что собой представляет коэффициент усиления по напряжению контура? Физическая сущность добротности контура?
Характеристическое сопротивление последовательного контура.
2. После выполнения работы
2.1.Какие пути достижения резонанса существуют? Какой из них эффективнее настраивает контур в резонанс?
2.2.Область применения резонанса напряжений на практике.
2.3.Достоинства и недостатки резонанса напряжений.
2.4.Проанализируйте векторную диаграмму (по указанию преподавателя) для одного из 3-х характерных режимов нагрузки.
2.5.Объясните сущность изменения сопротивлений в зависимости от индуктивности катушки.
2.6.Объясните сущность изменения тока, полного сопротивления, коэффициента мощности, падений напряжений на индуктивности и емкости (по указанию преподавателя) в зависимости от индуктивного сопротивления катушки.
ЛАБОРАТОРНАЯ РАБОТА № 3
РЕЗОНАНС ТОКОВ. ПОВЫШЕНИЕ КОЭФФИЦИЕНТА МОЩНОСТИ ЭЛЕКТРОУСТАНОВОК
Цель работы:
1. Ознакомиться с явлением резонанса токов в цепях переменного тока с параллельным соединением приемников.
2. Ознакомиться с методом искусственного повышения коэффициента мощности электроустановок при помощи конденсаторов.
ПРОГРАММА РАБОТЫ
1. Ознакомиться с оборудованием и приборами лабораторной установки ЛЭС-5.
2. Собрать электрическую схему (рис.3.7) и уяснить назначение отдельных элементов. Определить цену деления приборов.
3. Выполнить эксперимент по определению влияния параметров параллельной цепи "на амплитудно-фазовые соотношения между токами ветвей. Рассмотреть три характерных режима: преобладание индуктивной проводимости (Bl>Bc), емкостной проводимости (Bl<Bc) и резонанс токов (Вl =Вс).
4. Изучить методы искусственного повышения коэффициента мощности электроустановок при помощи конденсаторов.
5. Для каждого характерного режима (по указанию преподавателя) по результатам измерений построить векторные диаграммы (рис.3.2.-3.4).
6. По данным измерений и расчетов построить совмещенные графики функций:
1)Y=Y(C), В=В(С); BL=B(C); ВС=В(С); G=G(C); Z=Z(C) (рис.3.5)
2) I= I (Bc); IL= I (Bc); Ic= I (Bc); IR= I (Bc); Ix= I (Bc); cosj=cosj (Bc) (рис.3.6).
ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ
1. Резонанс токов
При параллельном соединении сопротивлений напряжения на каждой ветви одинаковы, общий ток равен сумме токов ветвей (рис.3.1).
Для анализа и расчета параллельных цепей графоаналитический метод из-за громоздкости и невысокой степени точности не удобен. Поэтому обычно используют метод комплексных проводимостей.
В цепях переменного тока существуют три проводимости: полнаяY, активнаяG и реактивная В. Y=G±jB — здесь знак «+» при емкостной, знак «- » при индуктивной проводимостях. Важно отметить, что выражение активной проводимости при синусоидальном токе отличается от выражения проводимости при постоянном токе (g= 1 / R) и зависит как от активного R, так и от реактивного X сопротивлений. Причем только полная проводимость является величиной обратной полному сопротивлению последовательного участка (ветви) цепи Z
Y=1/Z=I/U, Y1=1/Z1=I1/U, Y2=1/Z2=I2/U (3.3)
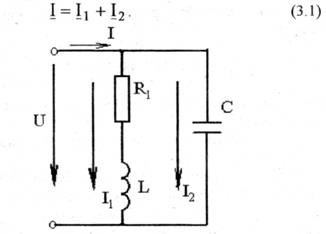
Рис. 3.1
Как известно, сопротивление ветви с катушкой индуктивности носит активно-индуктивный характерZ1=R1+jXL, с конденсатором, пренебрегая активным сопротивлением конденсатора из-за его небольшого значения -емкостный характер Z2 = R2- jXc = — jXc. Тогда комплексные проводимости ветвей соответственно равны Y1=G1-jBLиY2=jBc, а полная проводимость параллельной цепи определяется как их сумма
Y=Y1+Y2=G1-j(BL-Bc)=G-jB, (3.4)
гдеG1=R1/(R12+ XL2)=R1/ Z12, G2=R2/Z22 =0 иG=RЭ/(RЭ2+ XЭ2)–активные проводимости соответственно ветвей с индуктивностью L, емкостью С и всей цепи с эквивалентными активным Rэ и реактивным Хэ сопротивлениями;
BL=XL/(R12+XL2), Bc=Xc/(R22+Xc2)=1/Xc, иB=BL-Bc-реактивные проводимости соответственно ветвей с L и С и всей цепи.
Представим Y в показательной форме:
Y = Yejj, (3.5)
где Y=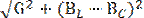 — полная проводимость;
— полная проводимость;
j=arctg((BL-BC)/ G) — аргумент полной проводимости (угол сдвига фаз).
Характер процессов, протекающих в параллельных цепях с индуктивностью и емкостью в ветвях, определяется соотношением между реактивными проводимостями этих ветвей. Это соотношение может принимать одно из следующих значений Bl>Bc, Bl=BcиBl<Bc. В этой работе изменение соотношения между проводимостями обеспечивается регулированием емкости, т. к. Вc=1/Xc=wC= 2pfC, где f и w — соответственно линейная и угловая частоты переменного тока.
1. В случае BL>Bc, т. е. XL/(R12+XL2)> 2pfC, что имеет место при изменении емкости ветви с 0 до С0 (рис.3.2; 3.5), всегда IL>Ic и реактивный ток Ix= IL — Ic> 0 индуктивный. Поэтому цепь обладает активно-индуктивной нагрузкой. Энергия, потребляемая из сети, расходуется на создание части магнитного поля катушки и нагрев активного сопротивления всех участков цепи.
Сдвиг по фазе 90° >j> 0, поэтому общий ток I цепи отстает по фазе от напряжения U (рис.3.2.).
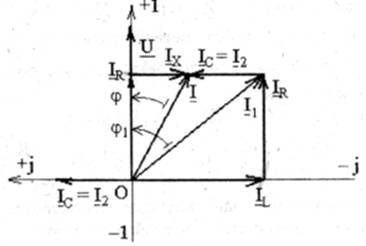
Рис. 3.2
2.В случае BL=Bc токи IL=Ic, угол сдвига фазы j=0 и cosj =1. Полная проводимость минимальна и равна активной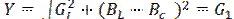 . Поэтому общий ток минимален и равен активномуIR=Icosj = I (рис.3.3, 3.5 и 3.6.), а реактивный ток Ix= IL-Ic=0. Характер нагрузки активный. Такой режим носит название резонанса токов. В этом случае токи в ветвях I1 и I2 значительно больше, чем ток в неразветвленной части цепи I (рис:3.6). Это свойство — усиление тока — является важнейшей особенностью резонанса токов и широко используется на практике.
. Поэтому общий ток минимален и равен активномуIR=Icosj = I (рис.3.3, 3.5 и 3.6.), а реактивный ток Ix= IL-Ic=0. Характер нагрузки активный. Такой режим носит название резонанса токов. В этом случае токи в ветвях I1 и I2 значительно больше, чем ток в неразветвленной части цепи I (рис:3.6). Это свойство — усиление тока — является важнейшей особенностью резонанса токов и широко используется на практике.
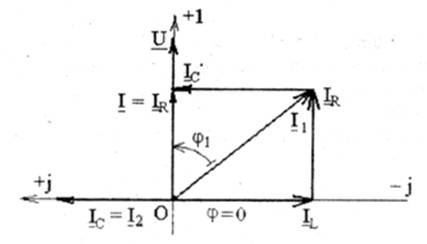
Рис. 3.3
Резонанс токов характерен тем, что энергия магнитного поля катушки индуктивности равна энергии электрического поля конденсатора, при этом происходит колебательный процесс их взаимного обмена внутри этой цепи, а энергия от источника расходуется только в активном сопротивлении R1.
Явление компенсации реактивного индуктивного тока используют для улучшения (компенсации) коэффициента мощности cosj в электроустановках.
3. В случае Bl<Вс, приС> С0, ток IL<Iс, а реактивный ток цепи Iх емкостной (Ix =Il–Ic<0) и цепь обладает активно-емкостным характером нагрузки (рис. 3.4-3.6). Полный ток цепи I опережает напряжение U на уголj при -90° <j< 0.
Энергия, потребляемая из источника, в этом случае расходуется на создание электрического поля конденсатора и нагрев активного сопротивления R1.
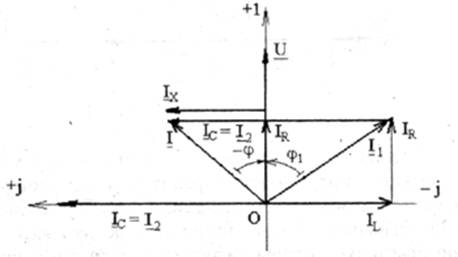
Рис. 3.4
2. Повышение коэффициента мощности электроустановок
Коэффициентом мощности называют отношение активной мощности Р к полной мощности S = UI
cosj=P/S=P/(UI). (3.6)
Коэффициент мощности показывает, какая доля электроэнергии необратимо преобразуется в активную, большая часть которой за вычетом потерь на нагрев идет затем на выполнение полезной работы (механической, лучистой, звуковой, тепловой и т. д.). Последнее учитывается через КПД установок.
Из приведенного отношения следует, что при одной и той же активной мощности Р приемников, если напряжение сети остается постоянным, то с уменьшением cosj потребляемый ток из сети возрастает за счет индуктивной составляющей. Тогда генераторы, трансформаторные подстанции загружаются полной мощностью за счет реактивной, но недоиспользуются по активной мощности. В то же самое время большой ток приводит к увеличенным потерям на нагрев проводов сети и обмоток генераторов (трансформаторов). Повышаются потери напряжения в сети, что нарушает нормальную работу других потребителей и тем самым вызывает необходимость замены проводов линии электропередач проводами увеличенного сечения, а генераторы на большую мощность, то есть приводит к дополнительным капитальным затратам.
Однако cosj предприятий сильно зависит как от характера нагрузки приемников (активный или активно-индуктивный), так и от степени их загрузки. Например, у асинхронных двигателей, трансформаторов при нормальной загрузке коэффициент мощности составляет 0,8. .0,9, который снижается до 0,2. .0,4при неполном использовании их мощности.
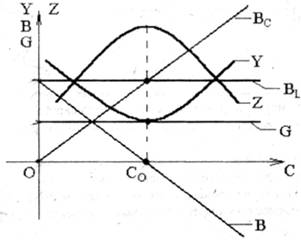
Рис. 3.5
До недавнего времени для предприятий нормировался минимально допустимый cosj в пределах 0,9…0,92. В настоящее время энергосистемой устанавливается допустимое значение реактивной мощности Qэ и нормируется tgjэ =Qэ/Рф. Фактическое значение tgjф определяется по показаниям счетчиков реактивной Wp и активной Wa энергии предприятия tgjф = Wp/Wa.
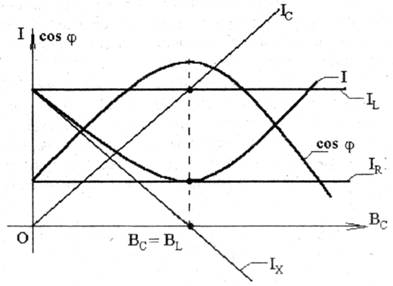
Рис. 3.6
Для повышения cosj электрических установок применяют ряд мер, направленных на компенсацию реактивной мощности. Увеличение cosj можно добиться следующими способами:
1) заменой малозагруженных двигателей (загрузка менее 45 %от номинальной) двигателями меньшей мощности;
2) понижением напряжения на обмотках малонагруженных двигателей, работающих треугольником, переключением их на звезду;
3) выключением двигателей и трансформаторов, работающих на холостом ходу;
4) включением в сеть специальных компенсирующих устройств, представляющих собой статические конденсаторы или синхронные компенсаторы (облегченные синхронные двигатели).
Наиболее простым и удобным аппаратом для улучшения cosj является статический конденсатор, включаемый параллельно с активно-индуктивной нагрузкой (рис. 3.1.). При включении конденсатора емкостный ток Iс, находящийся в противофазе с индуктивным током ILнагрузки, приводит к их взаимной частичной (рис. 3.2) или полной (рис. 3.3) компенсации. Общий ток I со значения I1 (конденсатор отключен) уменьшается до Ir (резонанс токов). Причем активная составляющая тока Ir, а тем самым и активная мощность Р, остаются без изменения. При этом угол сдвига фазjсоставляет 0£j<j1, а коэффициент мощности cosj повышается от cosj1 (см. рис. 3.2)до cosj=1 (при резонансе токов, см. рис.3.3).
Обычно мощные специальные конденсаторы называют косинусными и их маркируют не по току, а по реактивной мощности Q (квар) при определенном напряжении. Косинусные конденсаторы устанавливают на трансформаторные подстанции предприятия или у рубильников распределительных шкафов, шинных сборок цеха. Мощность компенсирующего устройства (батарей) Qб определяется как разность между фактической реактивной мощностью предприятия Qфи задаваемой энергосистемой оптимальной реактивной мощностью Qэ, т. е.Qб = Qф-Qэ= wCU2 = 2pfCU2 или Qб= Pф(tgjЭ — tgj1), вар, где Рф — фактическая активная мощность, Вт. (3.7)
Тогда требуемая емкость компенсирующих устройств
nC=(Pф106)/(2pfU2) (tgjэ-tgj1),мкФ (3.8)
где n — число фаз переменного тока;
U — напряжение на фазе (клеммах) конденсатора.
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
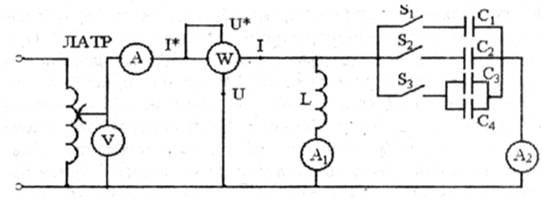
Рис. 3.7
Лабораторная работа проводится на установке ЛЭС-5, где необходимо задействовать (рис.3.7):
1.Лабораторный автотрансформатор ЛАТР (U=0…250 В и I£ 2 А) — 1 шт.
2.Вольтметр V (0…75.0 В) — 1 шт.
3.Катушка индуктивности без ферромагнитного сердечника (w=1200 витков) — 1 шт.
4.Батарея конденсаторов 0…94,75 мкФ (C1=0…34,75 мкФ; С2=30 мкФ, С3=20 мкФ, С4=10 мкФ). — 1шт
5.Однополюсные выключатели S1…S3 — 3 шт.
6.Амперметр 0…2,5 А (А, А1, А2) — 3шт.
7.Ваттметр W (I=2,5 A, U=75,0 В) — 1 шт.
ПОРЯДОК ПРОВЕДЕНИЯ ОПЫТОВ
1. Собирают электрическую схему согласно рис. 3.7. Ручку ЛАТРа устанавливают в исходное положение (до упора против часовой стрелки). Отключают выключатели S1, S2, S3. Переключатель пределов измерения вольтметра V и катушки напряжения ваттметра переводят на 75 В, амперметры А, А1, А2 устанавливают на 2,5 А, а токовую катушку ваттметра W подключают на 2,5 А.
2. После проверки схемы преподавателем или лаборантом включают питание ЛАТРа. Наблюдая за показаниями приборов, плавно повышают рукояткой ЛАТРа напряжение по вольтметру V до 50. . . 60 В. Записывают показания приборов в табл. 3.1.
3. Подключая конденсаторы с шагом 15…20 мкФ до суммарной емкости 94 мкФ, по амперметру А наблюдают за изменением общего тока цепи I. Общий ток сперва уменьшается (Bl>Bc), достигает минимального значения (BL=Bc — резонанс токов) и затем увеличивается (Bl<Bc). Отключают конденсаторы.
4. Повторно подключая конденсаторы с установленными по п. 3 значениями для соответствующих характерных режимов, записывают показания приборов в табл. 3.1.
Таблица 3.1
|
№ |
C |
U |
P |
I |
I1 |
I2=Ic |
Cosj |
Sinj |
j |
Характер режима |
|
мкФ |
В |
Вт |
А |
о. е. |
град |
|||||
|
1 2 3 |
0 20 40 |
BL>Bc |
||||||||
|
4 |
58 |
BL=Bc |
||||||||
|
5 6 |
75 94 |
BL<Bc |
5. Плавно снижают напряжение ЛАТРом и выключают питание. Через несколько минут выключатели S1, S2, S3 переводят в положение «Выкл.».
Таблица 3.2
|
№ |
BL=B1 |
Bc=B2 |
Y |
B |
G |
Z |
IL |
IR |
Ix |
|
Сим |
Ом |
А |
|||||||
|
1 |
|||||||||
|
2 |
|||||||||
|
3 |
|||||||||
|
4 |
|||||||||
|
5 |
|||||||||
|
6 |
ОБРАБОТКА ОПЫТНЫХ ДАННЫХ
1. Расчетные параметры в табл.3.1. и 3.2 определяют из следующих соотношений:
1.1 Коэффициент мощности цепи
cosj=P/UI, cosj1= P/UI (по данным, при С=0).
1.2. Реактивная (индуктивная) проводимость ветви с катушкой индуктивности
BL = (I1/U)sinj1= const, Сим,
гдеsinφ1находят по данным п.1.1 при С=0.
1.3.Реактивная (емкостная) проводимость ветви с конденсатором
Вс= I2/U, Сим.
1.4.Полная проводимость цепи
Y=1/Z = I/U, Сим.
1.5. Реактивная проводимость цепи
± В = BL — ВC, Сим.
1.6. Активная проводимость цепи
G = Y cosj, Сим.
1.7. Полное сопротивление цепи
Z=1/Y=U/I, Ом.
1.8. Реактивный индуктивный ток цепи (ветви с катушкой)
Il= I1sinj1 = const, А.
1.9. Активный ток цепи (ветви с катушкой)
IR= I cosj = I1cosj1= const, А.
1.10.Реактивный ток цепи±Ix = IL-Ic, А.
2. Векторные диаграммы строят для трех характерных режимов: резонанса токов, дорезонансного режима (BL>Bc) и после резонансного (Bl<Bc) (по пунктам табл.3.1. согласно указанию преподавателя) следующим образом.
Предварительно выбирают масштабы напряжения Мu (В/см) и токов MI (А/см), для наглядности оси вещественных чисел (+1) проводят вертикально, мнимых чисел (+j) — горизонтально влево. Для параллельной цепи опорным вектором является одинаковый для всех ветвей вектор напряжения источникаU=Uej0,совпадающий для удобства с вещественной осью(yu=0).
Построение векторной диаграммы начинают с вектора тока ветви с катушкой индуктивности I1= IR + IL. Для этого по вещественной оси откладывают ток IR, по мнимой — IL и достраивают вектор I1, . Откладывают по мнимой оси от начало координат вектор емкостного тока I2=Ic, который затем параллельно самой себе пристраивают к концу вектора I1. Из начала координат проводят до конца вектора Icвектор общего тока I = I1+Ic. Достраивают вектор тока Ix=Il-Ic. Обозначают углы сдвига фаз jи j1.
3. По данным табл.3.2 строят совмещенные графики функций проводимостей Y; В; BL; Вс; G, полного сопротивления Zв зависимости от емкости конденсатора С (рис. 3.5).
4. По данным таблицы 3.1 и 3.2 строят совмещенные графики функций токов I; IL; Ic;Ir;Ix и cosj в зависимости от реактивной емкостной проводимости Вс (рис.3.6).
5. По векторным диаграммам для характерных режимов и графикам функций в зависимости от емкости и реактивной емкостной проводимости проводят анализ работы параллельной цепи.
6. По полученным результатам опытов уясняют метод искусственного повышения коэффициента мощности электроустановок с активно-индуктивной нагрузкой при помощи конденсаторов (рис.3.2; 3.3; 3.5; 3.6) . По заданному преподавателем cosjэ, на базе опытных данных, определяют реактивную мощность конденсаторной батареи Qби требуемую для этого емкость конденсаторов как для однофазной, так и трехфазной цепи.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Перед выполнением опытов
1.1.Какова особенность цепей с параллельным включением приемников?
1.2.Какие проводимости имеют место в параллельных цепях постоянного и переменного токов?
1.3.Явление резонанса токов. Условие наступления резонанса токов. По какому признаку определяется возникновение резонанса токов?
1.4.Какие характерные режимы работы имеют место в параллельных цепях и как их практически установить? Какие из них чаще всего встречаются на практике?
1.5.Почему при резонансе ток ветви с катушкой несколько больше тока конденсатора?
1.6.Определение и физический смысл коэффициента мощности.
1.7. Какие способы повышения коэффициента мощности существуют?
2. После выполнения работы
2.1. Какие пути достижения резонанса токов существуют? Применение этого явления на практике.
2.2.Достоинства и недостатки резонанса токов.
2.3.По указанию преподавателя проанализируйте векторную диаграмму для конкретного характерного режима работы параллельной цепи.
2.4.Объясните сущность изменения емкостной, реактивной и полной проводимостей, а также полного сопротивления цепи от изменения емкости конденсаторной батареи.
2.5.Проанализируйте характер изменения, указанных преподавателем, токов цепи, их составляющих и коэффициента мощности в функции от реактивной емкостной проводимости.
ЛАБОРАТОРНАЯ РАБОТА № 4
ТРЕХФАЗНАЯ ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ ПРИ СОЕДИНЕНИИ ПРИЕМНИКОВ ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ ЗВЕЗДОЙ
Цель работы:
Изучить влияние изменения нагрузки на примере однофазных активных приемников на параметры трехфазной цепи.
ПРОГРАММА РАБОТЫ
1. Ознакомится с оборудованием, приборами лабораторной установки, записать их паспортные данные.
2. Собрать электрическую схему установки и уяснить назначение ее отдельных элементов (см. рис.4.8). Определить цену деления приборов.
3. Исследовать режимы, указанные в таблице. Установить влияние нулевого провода на работу системы.
4. Построить для каждого режима работы совмещенные топографическую (потенциальную) диаграмму напряжений и векторную диаграмму токов.
5. Проанализировать полученные результаты.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Совокупность трех однофазных цепей, в каждой из которых действуют синусоидальные ЭДС одинаковой частоты и амплитуды, отличающиеся по фазе одна от другой на 1200 и индуктируемые в одном источнике энергии, называется симметричной трехфазной системой или трехфазной цепью. Каждая из однофазных цепей называется фазой трехфазной системы. Необходимо иметь ввиду, что фазой также принято обозначать угол сдвига одного электрического параметра относительно другого.
Трехфазная цепь состоит из трехфазного синхронного генератора
(рис. 4.1), создающего трехфазную систему ЭДС, линии передач и приемников (потребителей энергии или нагрузки), которые могут быть как трехфазными (например, электродвигатель), так и однофазными (например, лампы накаливания).
Три одинаковые по частоте и амплитуде, сдвинутые по фазе на 120 °, ЭДС получаются в трехфазных синхронных генераторах, установленных на подавляющем большинстве крупных электростанций. Простейший синхронный генератор имеет на статоре 1 три одинаковые фазные обмотки (А-Х, B-Y, C-Z), сдвинутые в пространстве на угол 120° относительно друг друга. При вращении ротора 2, выполненного в виде постоянного электромагнита (обмотка ротора, непоказанная на рисунке, включена в цепь постоянного тока), в обмотках статора индуцируется три синусоидальные ЭДС (еА, еВ, еС) одинаковой частоты и с равными амплитудами, сдвинутые по фазе относительно друг друга на 120° (рис. 4.2).
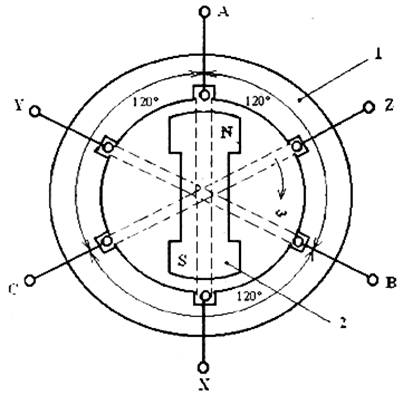
Рис. 4.1
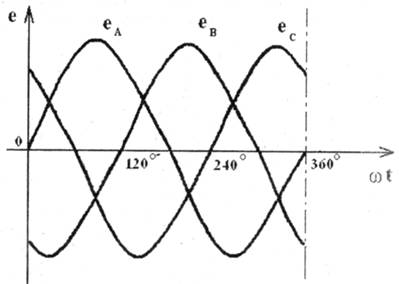
Рис. 4.2
Если начальную фазу ЭДС еА принять равной нулю, то мгновенные значения ЭДС можно записать:
еА =Еmsinwt;
еВ = Еmsin (wt — 120°);
еС = Еmsin (wt + 120°).
В комплексной форме действующие значения этих ЭДС:
EA=Eej0;
Ев=Ее-j120°;
Ес=Ееj120°.
Так как комплексному числу соответствует вектор на комплексной плоскости, то трехфазная система ЭДС может быть изображена в виде трех векторов (рис.4.3), сдвинутых на угол 1200 относительно друг друга. (Ось действительных величин +1 при расчете трехфазных систем принято направлять вертикально).
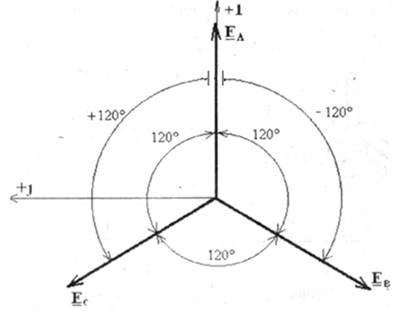
Рис. 4.3
Обмотки фаз генератора обычно соединяют звездой, т. е. концы обмоток X, Y, Z соединяют в общую точку N, называемую нулевой или нейтральной. При этом от трехфазного генератора отходят 4 провода: три линейных от точек А, В, С и нейтральный от точки N. В трехфазных четырех проводных сетях нейтральный провод заземляют.
Однофазные приемники также могут соединяться звездой, т. е. их концы х, у, z соединяют в общую точку п (рис.4.4) и присоединяют к нейтральному проводу, отходящему от точки N генератора, к свободным началам фаз приемника а, в, с подводят энергию по линейным проводам Аа, Вв, Сс от трехфазного генератора. Напряжения Ua, Ub, Uc между линейными и нейтральным проводом, т. е. между началом и концом фазы генератора (А-Х, B-Y, C-Z), называются фазными напряжениями генератора (источника). Причем UA+ Uв + Uc = 0.
Напряжения Ua, Ub, Uc между линейными и нейтральным проводом, т. е. между началом и концом фазы приемника (а-х, b-y, c-z), называются фазными напряжениями нагрузки.
Напряжения Uab, Ubc, Uca между линейными проводами, т. е. между началами фаз генератора, называются линейными напряжениями генератора. Соответственно для линейных напряжений приемника имеем: Uab, Ubc, Uca.
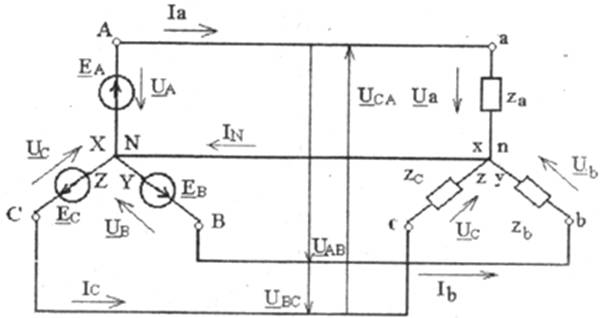
Рис. 4.4
Как видно из рис.4.5 напряжение Uab ( разность потенциалов точек А и В) равно ЕА — Ев (потенциал точки А равен ЕА, точки b равен Ев) или
Uab = Ua-Ub. (4.1)
Аналогично получаем выражения для двух других напряжений:
Uac = Ub–Uc; Uca = Uc–Ua. (4.2)
В соответствии с (4.1) построим векторную диаграмму линейного напряжения Uab на комплексной плоскости (суммируя вектор UAс вектором-UB) (рис.4.6).
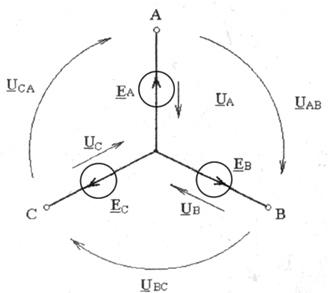
Рис. 4.5
Аналогично строим векторы Ubc и Ucaв соответствии с (4.2). Из векторной диаграммы видно, что векторы линейных напряжений также образуют симметричную трехфазную систему, т. е. их действующие значения Uл одинаковы и сдвинуты относительно друг друга по фазе на угол 120°. В комплексной форме линейные напряжения можно записать:
UAB=Uлеj30°; UBС=Uле-j90°; UСА=Uлеj150°, (4.3)
где Uл — действующие значение линейного напряжения.
Связь между линейными и фазными напряжениями можно получить, выделив на векторной диаграмме (рис.4.6) треугольник, образованный векторами Uab, Ua, Ub. Стороны этого равнобедренного треугольника соответственно равны Uл и Uф, откуда следует, что
Uл=2Uфcos 30° = Uф![]() (4.4)
(4.4)
От векторной диаграммы можно перейти к топографической (потенциальной) диаграмме напряжений, приняв потенциал точки N равным нулю.
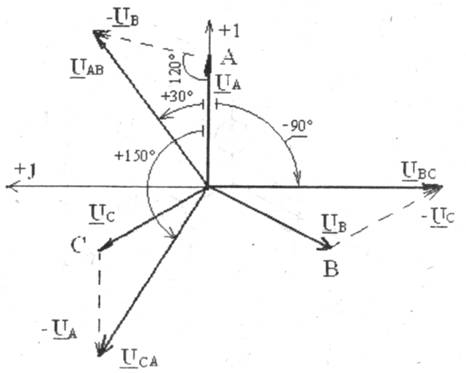
Рис. 4.6
Перенесем вектор линейного напряжения Uab (рис. 4.6) параллельно самому себе так, чтобы начало вектора переместилось в точку А (рис. 4.7). Аналогично перенесем векторы Ubс и Uсa. Векторы Uab, Uвси Uсаобразуют замкнутый треугольник линейных напряжений, при этом каждой точке на схеме соответствует потенциал на комплексной плоскости (обратите внимание, что на схеме рис.4.5 стрелка, показывающая положительное направление напряжения между двумя точками, например, Uab направлена от точки Ак точке В, а на комплексной плоскости вектор UАВ направлен от точки В к точке А, т. е. в точку большего потенциала, как и должно быть на топографической диаграмме. То же самое относится и к фазным напряжениям на топографической диаграмме).
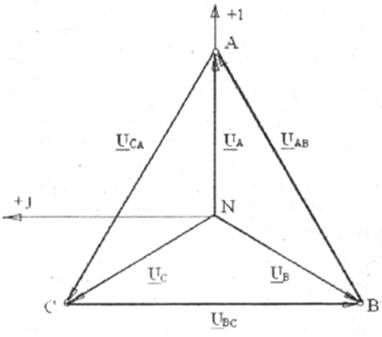
Рис. 4.7
Токи, протекающие в линейных проводах, называются линейными Iл, в обмотках генератора или фазах приемника фазными Iф. При соединении звездой обмотки генератора, линейный провод и фаза приемника соединяются последовательно, поэтому Iл=Iф. Применяя к узлу N первый закон Кирхгофа, получаем ток в нулевом проводе
IN=Ia+Ib+Ic. (4.5)
Трехфазный приемник электрической энергии также соединен звездой, причем система может быть четырехпроводной (когда концы обмоток генератора, соединенные в общую точку N, соединяются проводом с точкой n, в которой соединены концы фаз приемника) или трехпроводной, когда отсутствует нулевой провод.
1. Схема соединений звезда-звезда с нейтральным (нулевым) проводом
Для четырехпроводной системы, представленной на рис. 4.8. (ключ S3 замкнут), фазные напряжения приемника равны фазным напряжениям генератора (конечно, если сопротивлениями линейных и нейтрального проводов можно пренебречь), т. е. Uа = UA; Ub = Uв; Uс = Uc. Соответственно равны между собой и линейные напряжения генератора и приемника.
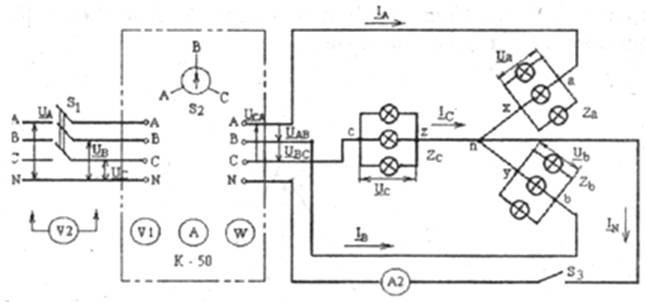
Рис. 4.8
Режим работы каждой фазы приемника не зависит от режима работы двух других фаз — ток определяется параметрами приемника только этой фазы.
Ia=Ua/Za;Ib=Ub/Zb; IC=UC/ZC,
где Za,Zb,Zc — комплексные сопротивления фаз приемника. Ток в нейтральном проводе равен сумме трех фазных токов
IN=Ia+Ib+Ic.
Векторная диаграмма токов, совмещенная с топографической диаграммой напряжений, имеет вид, представленный на рис 4.9, а. Ток в нейтральном проводе находится согласно уравнению (4.5), графическая интерпретация которого представлена на этом же рисунке (4.9, б).
Частным случаем нагрузки трехфазной системы является случай симметричной (равномерной) нагрузки, когдаZa = Zb = Zc=Zфеjj. В этом случае токи в фазах будут одинаковыми и сдвинутыми по фазе относительно соответствующих фазных напряжений на один и тот же угол φ. Векторная диаграмма токов, совмещенная с топографической диаграммой напряжений, имеет вид, представленный на рис.4.10. Ток в нейтральном проводе отсутствует, т. к. нагрузка симметричная. Поэтому нейтральный провод для таких потребителей не применяется (трехфазные двигатели, нагреватели и т. д.).
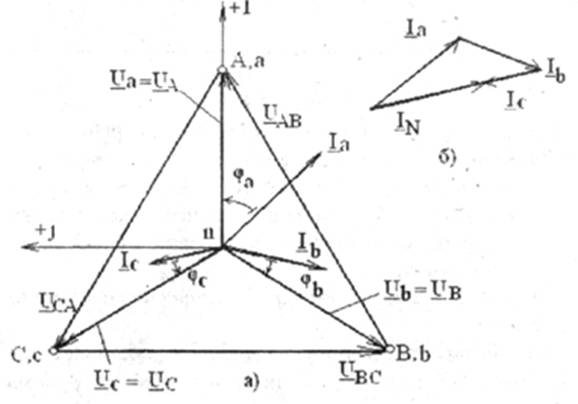
Рис. 4.9
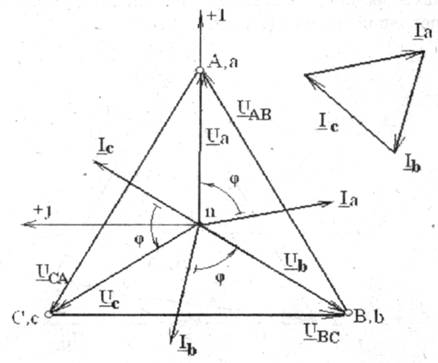
Рис. 4.10
2.2. Схема соединений звезда-звезда без нейтрального провода
Отсутствие нейтрального провода (см. рис.4.8 при отключенном ключе S3) значительно нарушает симметрию фазных напряжений приемника при несимметричной нагрузке, хотя при симметричной нагрузке совмещенная топографическая и векторная диаграмма ничем не отличается от четырех-проводной системы (см. рис.4.10).
В случае несимметричной нагрузки в той фазе, где комплексное сопротивление больше, фазное напряжение приемника повышается относительно фазного напряжения генератора. И наоборот, напряжение снижается на фазных приемниках, у которых сопротивление меньше.
Такое отклонение напряжения на приемниках является не нормальным, так как в первом случае оно может за счет повышенного напряжения вывести из строя потребители, а во втором случае может привести к нарушению технологического режима работы оборудования (снижение оборотов у двигателей, недонакал ламп и т. д.).
Потенциал нейтральной точки приемника уже не будет равен нулю (см. рис. 4.11, 4.12, 4.13).
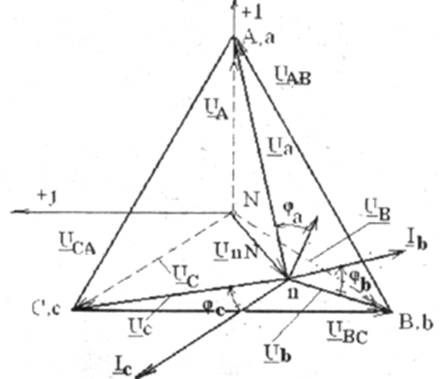
Рис. 4.11
Его можно найти методом двух узлов (пи N), но в комплексной форме, пренебрегая из-за малости проводимостями соединительных проводов и обмоток источника
UnN=(YaUA+YbUb+YcUC)/(Ya+Yb + Yc), (4.6)
гдеYa=1/Za;Yb = 1/Zb,Yc = 1/Zc — комплексные проводимости фаз приемника.
Комплексные значения напряжений на нагрузке при нарушениях симметрии напряжения определяются следующими равенствами:
Ua=UA-UnN;Ub=UB-UnN;Uc=UC-UnN.
Фазные токи при этом равны:
Iа=Uа/Zа;Ib=Ub/Zb;Ic=Uc/Zc
и связаны между собой уравнением
Iа+Ib+Ic=0.
Для исключения нарушения симметрии напряжений на фазных приемниках (несимметричный режим, включая обрыв фазы, характерный для осветительной и бытовой нагрузки) на практике предусматриваются меры, исключающие обрыв нейтрального провода. При этом в цепь нейтрального провода не ставят выключатели, предохранители и другие устройства, которые могли бы привести к его разрыву.
Крайними случаями нарушения симметрии, фазных напряжений нагрузки являются обрыв (на рис.4.12 обрыв фазы «а» Za=¥) и короткое замыкание фазы (на рис.4.13 короткое замыкание фазы «о» Za=0).
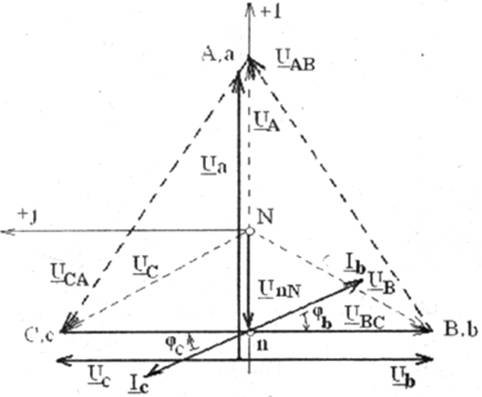
Рис. 4.12
Проводимость оборванной фазы Ya=0, проводимости неповрежденных фаз не изменяются. Смещение нейтральной точки согласно (4.6), при Yb=Yс
UnN=(UA*0+UBYb+UCYc)/(0+Yb+Yc)=
=Yф(UB+UC)/(2Yф)=-UA/2=-(127/2)ejo=-63,5 ejoB.
В случае короткого замыкания (рис. 4.13) напряжение на приемниках возрастает до значения линейного напряжения, т. е. в 1,73 раза, т. к. потенциал точки «n» равен потенциалу точки «а» и на топографической диаграмме точка «n» совпадает с точкой «а» иUnN=Ua=127ejoB.
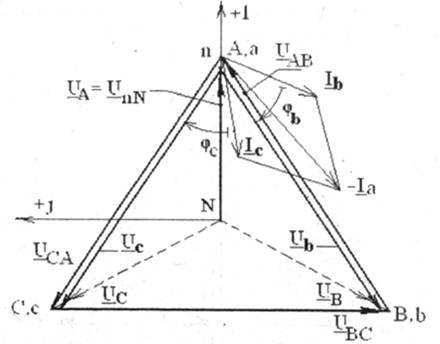
Рис. 4.13
ОПИСАНИЕ ЭКСПЕРЕМЕНТАЛЬНОЙ УСТАНОВКИ
Схема экспериментальной установки для исследования трехфазной электрической цепи приведена на рис. 4.8. Трехфазный приемник представляет собой активную нагрузку, соединенную звездой, в каждой фазе которой использованы ламповые реостаты с выводами а-х, в-у, c-z. С пятью параллельно включенными лампами одинаковой мощности и напряжения.
Для измерения фазных токов IA=Iа, IB=Ib, IC=Ic, активных мощностей фазных приемников РA=Ра, РB=Рв, РC=Рс(только при наличии нейтрального провода) и напряжений генератора UA, UB, UC применяется измерительный комплект К-50, который переводится для измерения вышеуказанных параметров с одной фазы на другую переключателем S2 (приборами Al, W и V1). Вольтметром V2 со свободными концами поочередно измеряют:
— трехфазные напряжения нагрузки Ua, Ub, Uc на зажимах а-х, в-y, c-z приемников;
— линейные напряжения Uab=UAB, Ubc=UBC, Uca=UCA на зажимах а-в, в-с, с-а приемников (или А-В, В-С, С-А измерительного комплекта К-50);
— напряжение UNn между нейтральными точками генератораN и нагрузки nпри отключенном ключе S3.
Амперметром А2 при включенном ключе S3 измеряют ток Inв нулевом проводе.
ПОРЯДОК ПРОВЕДЕНИЯ ОПЫТОВ
1. Собирают схему согласно рис. 4.8.
2. Убедившись в правильности собранной схемы, включают S1 питание приемника. Проводят измерения, для удобства изменяя сопротивление только в одной фазе, например, Raпри следующих режимах работы цепи:
— равномерная (симметричная) нагрузка фаз Ra=Rb=Rc;
— неравномерная (несимметричная) нагрузка фаз Ra>Rb=Rc
— обрыв в фазе "а", когда Ra=¥, Rb=Rc;
— короткое замыкание фазы "а", когда Ra=0, Rb=Rc.
Указанные режимы добиваются параллельным включением между собой по фазам ламп накаливания одинаковой паспортной мощности и напряжения. Наличие или отсутствие нейтрального (нулевого) провода достигается соответственно замыканием или размыканием цепи нейтрального провода с помощью ключа S3. Обрыв фазы "а" соответствует случаю, когда в этой фазе все лампы отключены. Режим короткого замыкания в фазе "а" достигается замыканием (шунтированием) зажимов а-х соединительным проводом. Необходимо помнить, что режим короткого замыкания проводится при отключенном нейтральном проводе, когда ключ S3 разомкнут. В противном случае в цепи произойдет аварийное короткое замыкание.
Все данные заносят в таблицу.
ОБРАБОТКА ОПЫТНЫХ ДАННЫХ
1.По результатам измерений вычисляют активную мощность трехфазного приемника при различных режимах работы, как сумму активных мощностей фазных нагрузок, полученных при наличии нейтрального провода
Р=Ра+Рb+Рс.
2.Находят проводимости фаз приемника
Ya=l/Za=Ia/Ua;Ya=Ia/Ua;
Yb=1/Zb=Ib/Ub; Yb=Ib / Ub;
YC=1/Zc = Ic/Uc; Yc=Ic/Uc,
где Ia, Ib, Ic, Ua, Ub, Uc — действующие значения фазных токов и напряжений соответственно, измеряемые приборами.
3.По опытным и расчетным данным таблицы определяют расчетное значение напряжения между нейтральнымиточками генератора и нагрузки
UnN= (YaUA+YbUB+YcUC) / (Ya+Yb+Yc).
4. По данным таблицы строят совмещенную топографическую и векторную диаграммы напряжений и токов для всех четырёх режимов при отключенном нейтральном проводе. Построение диаграммы начинают, приняв удобный масштаб напряжений, с построения равностороннего треугольника векторов линейных напряжений Uл=Uab:=Ubc:=Uca, которые не зависят от режима нагрузки (табл.4.1). В треугольнике достраивают векторы фазных напряжений генераторов Uф=Uaв=Ubс=Ucа, началом которых является центр тяжести точки N равностороннего треугольника. С вершин равностороннего треугольника делают засечки радиусами, равными в масштабе соответствующим фазным напряжениям нагрузки Ua, Ub, Uc. Из точки N (нейтральная точка генератора) делают засечку радиусом UnhОбщая точка пересечения дуг (точка пна рис.4 14, 4.15, 4.16, 4.17) определяет потенциал точки п нагрузки относительно точки N генератора.
Для активной нагрузки, каковыми являются лампы накаливания, векторы токов в фазах совпадают с векторами соответствующих фазных напряжений по фазе (jа=jb=jс=0). При отсутствии нейтрального провода векторная сумма фазных токов, сходящихся в узле п, равна нулю, т. е. Ia+Ib+Ic=0 (см. рис. 4.14…4.17).
5. На основании построенных совмещенных топографических и векторных диаграмм определить углы (yu)a, (yu)в, (yu)с и (yu)N и сравнить их с расчетами:
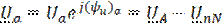 ,
,
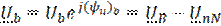 ,
,
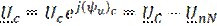 ,
,
![]()
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. До выполнения работы
1.1.Дайте определение схемы соединения приемников звездой. В каких случаях потребители соединяются звездой?
1.2.Покажите на схеме, где течет линейный и фазный токи?’ Каково соотношение между ними?
1.3.Почему опыт короткого замыкания должен проводиться при строго отключенном нулевом проводе?
1.4.Покажите на схеме, между какими точками измеряют линейное и фазное напряжения, напряжение между нейтральными точками?
Каково соотношение между ними для генератора?
2.После выполнения работы
2.1.Какова роль нейтрального провода? Сформулируйте требования к нему.
2.2.Как отличаются между собой векторные диаграммы с нейтральным проводом и без него при режимах:
— симметричный,
— несимметричный,
— обрыв фазы,
— короткое замыкание в фазе.
2.3. Как определяется мощность в трехфазной цепи? Какова она при различных режимах?
2.4 В чем преимущество трехфазных цепей по сравнению с однофазными?
Таблица
|
Режимы нагрузки (лампы по фазам na-nb-nc) |
Состояние нейтрального провода (ключ S3) |
Измерено |
Вычислено |
||||||||||||||||||||
|
Напряжения |
Токи |
Активная мощность |
∑P |
Проводимость |
Uл / Uф |
||||||||||||||||||
|
Линейные Uл |
Фазные Uф |
UnN |
Io |
Pa |
Pb |
Pc |
Ya |
Yb |
Yc |
||||||||||||||
|
UAB |
UBC |
UCA |
источника |
нагрузки |
IA |
IB |
IC |
||||||||||||||||
|
UA |
UB |
UC |
Ua |
Ub |
Uc |
||||||||||||||||||
|
В |
А |
Вт |
Сим |
||||||||||||||||||||
|
Равно-мерная (5-5-5) |
Вкл |
||||||||||||||||||||||
|
Выкл |
|||||||||||||||||||||||
|
Нерав-номерная (3-5-5) |
Вкл |
||||||||||||||||||||||
|
Выкл |
|||||||||||||||||||||||
|
Обрыв в фазе «а» (0-5-5) |
Вкл |
||||||||||||||||||||||
|
Выкл |
|||||||||||||||||||||||
|
Короткое замык-ание в фазе «а» (5-5-5) |
Вкл |
||||||||||||||||||||||
|
Выкл |
ЛАБОРАТОРНАЯ РАБОТА № 5
ЦЕПЬ ТРЕХФАЗНОГО ТОКА С ТОКОПРИЕМНИКАМИ, СОЕДИНЕННЫМИ ТРЕУГОЛЬНИКОМ
Цель работы:
Ознакомиться с работой 3-х фазной цепи, состоящей из однофазных ламповых приемников, соединенных треугольником, при различных режимах.
ПРОГРАММА РАБОТЫ
1. Собрать электрическую схему (см. рис.5.1).Определить цену деления.
2. Провести измерения при следующих режимах работы:
— равномерная нагрузка фаз;
— неравномерная нагрузка фаз;
— обрыв одной из фаз при равномерной нагрузке;
-обрыв одного линейного провода при равномерной нагрузке.
Результаты измерений занести в таблицу
3. Для каждого режима работы построить совмещенные топографические диаграммы напряжений и векторные диаграммы токов.
4. Проанализировать полученные результаты.
ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ
На рис.5.1 показана схема соединения приемников треугольником. Сопротивлениям фаз приемника при этом присваивается двойной индекс Zab, Zbc, Zca.
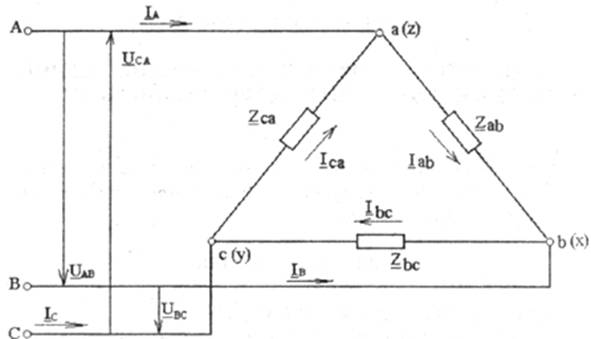
Рис 5.1
Каждая фаза приемника оказывается включенной на линейное напряжение генератора, поэтому фазные напряжения приемника равны линейным напряжениям генератора:Uab=UAB; Ubc=UBC; Uca=UCA.
Токи в проводах между генератором и приемником IA,IB,ICназываются линейными, их положительное направление — от генератора к приемнику. Токам в фазах присваивается двойной индекс Iab,Ibc,Iса, и положительные направления токов принимаются по часовой стрелке (по направлению фазных напряжений приемников).
Линейные и фазные токи связаны между собой первым законом Кирхгофа:
для узла "a" IA + Ica — Iab = 0,
для узла "в" Iab + IB — Ibc =0, (5.1)
для узла "с" IC + Ibc-Ica = 0.
3.1. При симметричной нагрузке фаз
Zab=Zbc=Zca=Zф=Zфejj,
действующие значения фазных напряжений равны действующим значениям линейных напряженийUав = UAB = Uл, Uвс=UBC=Uл, Uса=UCA=Uл.
Комплексные фазные напряжения при этом:
Uав = UAB = Uл e+ j30°,
Uвс=UBC=Uл e — j90°, (5.2)
Uса=UCA=Uл e+ j150°.
Действующие значения фазных токов одинаковы Iab=Ibc=Iсаи в зависимости от характера сопротивлений фаз отстают или опережают соответствующие фазные напряжения на один и тот же угол (или совпадают с последним при активной нагрузке, что и имеет место при ламповой нагрузке)
Iab=Uав / Zab
Ibc=Uвс / Zbc (5.3)
Iса=Uса/ Zca
Линейные токи располагаются согласно (5.1).
Диаграмма для симметричной нагрузки представлена на рис.5.2 для случая активно-индуктивной симметричной нагрузки.
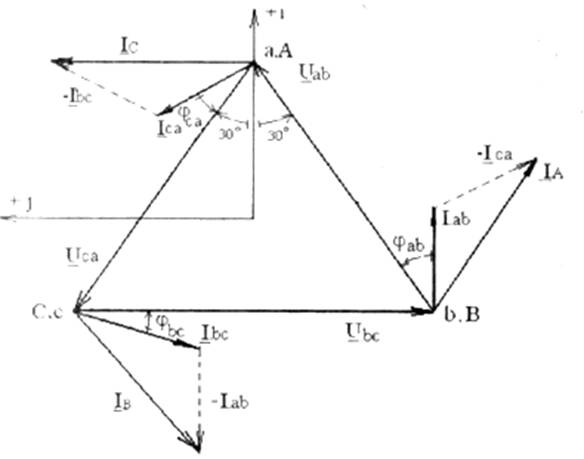
Рис. 5.2
3.2.При неравномерной нагрузке фаз
Zab¹Zbc¹Zca
действующие значения фазных напряжений равны между собой и равны линейным напряжениям
Uab=Ubc = Uca=Uл,
и в комплексной форме соответствуют (5.2).
Фазные токи определяются по (5.3), и их действующие значения уже не равны между собой, как это было в случае симметричной нагрузки. Угол сдвига фаз между векторами фазного тока и фазного напряжения для каждой фазы будет свой. В этом случае совмещенная диаграмма примет иной вид (см. рис.5.3).
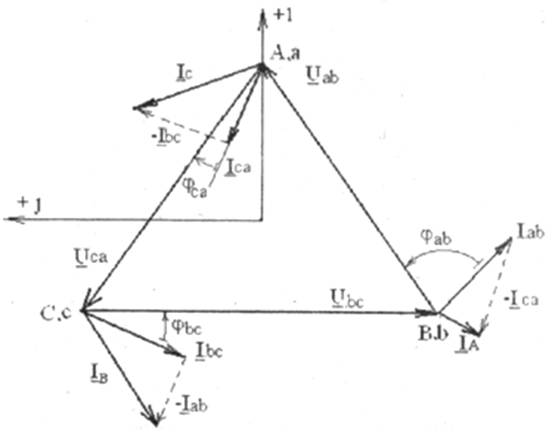
Рис. 5.3
3.3.При обрыве одной из фаз
При обрыве фаз (например, фазы "ав") у симметричного трехфазного приемника (рис.5.4) токи в неповрежденных фазах не изменятся, так как фазные напряжения, равные линейным, не меняются.
Линейные токи из (5.1), при Iab= 0
IA=-Ica; IB=Ibc; IC=Ica-Ibc (5.4)
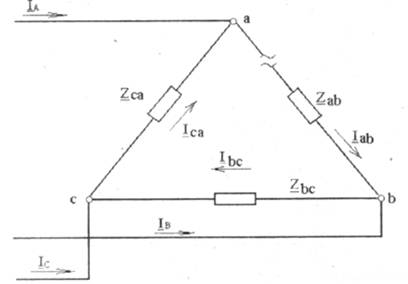
Рис. 5.4
Из этих уравнений следует, что действующие значения линейных токов IА и IB равны своим фазным токам, а действующее значение линейного тока IC не изменится и будет таким же, как и при отсутствии обрыва фазы "ав" (рис.5.5).
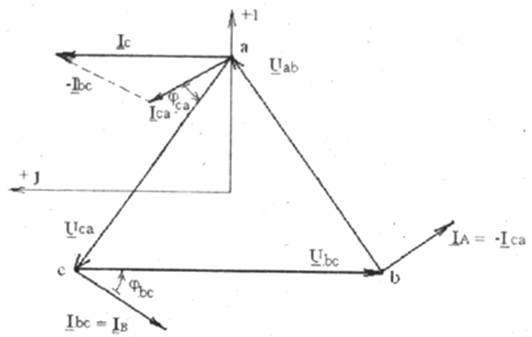
Рис. 5.5
3.4. Обрыв линейного провода
При обрыве линейного провода (например, в линии А-а) в симметричном трехфазном приемнике (рис.5.6), к приемнику будет подводиться только напряжение Ubc=UBC=Uлe-j90°. При этом сопротивление фазы "bc" подключено на полное напряжение Ubc, а равные сопротивления фаз "ab" и "са" подключены последовательно, и к каждому из них подведена половина линейного напряжения
Uab=Uca=-Ubc / 2=(Uл / 2) e — j90°.
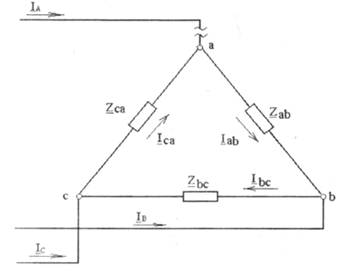
Рис. 5.6
Ток в фазе "bc" не меняется
Ibc=Ubc / Zbc,
а токи в других фазах и линейные токи находят из (5.1), при
Ica=Iab =Ubc / (2Zф):
Совмещенная диаграмма для этого случая представлена на рис. 5.7.
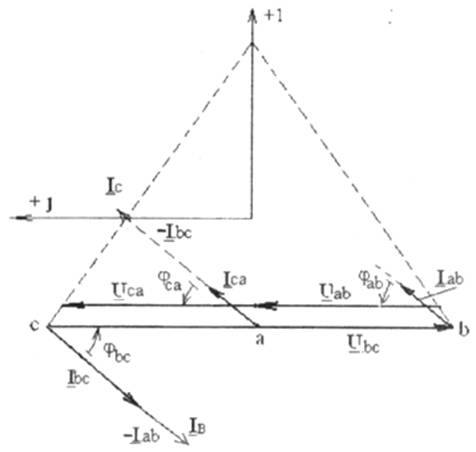
Рис. 5.7
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
Схема экспериментальной установки приведена на рис.5.8. Трехфазный приемник представляет собой активную нагрузку, соединенную треугольником, в каждой фазе такой нагрузки использован ламповый реостат с выводами а-х, в-у, c-z. Для измерения линейных токов IА, Iв, Iс, фазных напряжении генератораUA, Ub, Uc, активных мощностей фаз источника Ра, Рв, Рс применяется измерительный комплект К-50, который переводится с одной фазы на другую переключателем S2. С помощью амперметров Al, А2, A3 измеряются фазные токи соответственно Iab, Ibc, Icaв приемниках, вольтметром V2 со сводными концами поочередно измеряют три фазных напряжения нагрузки Uab, Ubc, Uca на зажимах а-х (в), в-у (с), c-z (а) приемников.
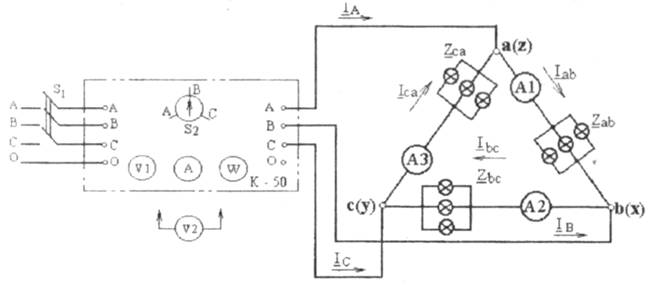
Рис. 5.8
ПОРЯДОК ПРОВЕДЕНИЯ ЭКСПЕРИМЕНТА
1. Собрать схему согласно рис. 5.8.
2. Убедившись в правильности собранной схемы, ключом S1 включить питание приемника. Измерения проводятся при следующих режимах работы электрической цепи:
— равномерная (симметричная) нагрузка фаз обеспечивается параллельным включением между собой в каждой фазе одинакового количества ламп «n» одной и той же мощности и напряжения (nab=5; nbc=5; nca=5)
Rab=Rbc=Rca;
— неравномерная (несимметричная) нагрузка фаз (nab=3; nbc=5; nca=5)
Rab¹Rbc=Rca;
-обрыв фазы "ab" при равномерной нагрузке остальных фаз (nbc=5; nca=5).
— обрыв линейного провода "A" при равномерной нагрузке фаз (nab=5; nbc=5; nca=5).
Обрыв фазы "ab" осуществляется размыканием цепи этого фазного приемника при отключенном напряжении источника при равномерной нагрузке в остальных фазах.
Обрыв линейного провода "А" достигается размыканием линии А-а (предварительно отключив питание) при равномерной нагрузке фаз.
Результаты измерений заносятся в таблицу 5.1.
ОБРАБОТКА ОПЫТНЫХ ДАННЫХ
1. По результатам измерений вычисляют активную мощность приемника, которая равна активной мощности источника питания, а она складывается из активных мощностей отдельных фаз источника, т. е.
P=Pab+Pbc+Pca=PA+PB+PC
2. Рассчитывают активные сопротивления фазных приемников Rab, Rbc, Rca
Rab=Uab / Iab, Rbc=Ubc / Ibc, Rca=Uca / Ica.
3. По данным таблицы для каждого режима работы цепи строят совмещенные топографические и векторные диаграммы напряжений и токов.
Для построения векторных диаграмм выбирается масштаб напряжений и токов. Построение векторной диаграммы напряжений начинают с построения равностороннего треугольника векторов линейных напряжений источника, которые не зависят от режима нагрузки
UAB = Uлe+j30°,
UBC=Uлe-j90°,
UCA=Uлe+j150°.
Следовательно, для первых 2-х режимов (равномерной и неравномерной нагрузок) треугольник фазных напряжений приемника будет таким же, как треугольник линейных напряжений источника.
5.1. При равномерной (симметричной) нагрузке фазные токи приемника равны и совпадают по направлению с фазными напряжениями, т. к. нагрузка активная (рис.5.9), то линейные токи находим согласно (5.1).
5.2.
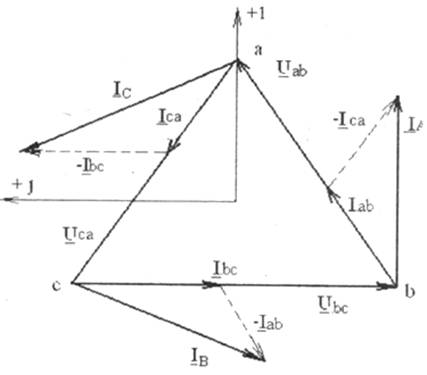
Рис. 5.9
3.2. Отличие векторной и топографической диаграмм при неравномерной нагрузке будет лишь в том, что токи в фазах уже неравны, что приведет к неравенству линейных токов.
3.3. При обрыве одной из фаз, в нашем случае фазы "ab" (см. рис. 5.4.), при равномерной нагрузке в двух других фазах, треугольник напряжений не изменится, и при Iab=0 построение ведется согласно (5.4) (см. рис. 5.10).
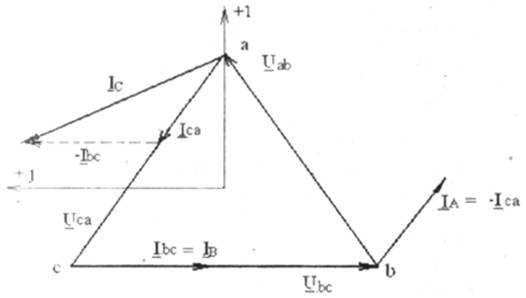
Рис. 5.10
3.4. При обрыве линейного провода, в нашем случае в линии А-а (см. рис.5.6), при равномерной нагрузке приемника к приемнику будет подводиться только, напряжение Ubc=UВС, а равные сопротивления фаз "ab" и "са" оказываются подключенными последовательно, на напряжение 0,5 Uл.
ПриIА=0 Ica=Iab=Ubc/2Zф,
и совпадают по направлению с соответствующими напряжениями в фазах приемника; ток в фазе "bc" не меняется
Ibc=Ubc/2Zbc,
а линейные токи строят согласно (5.5) (см. рис.5.11).
Обрыв линейного провода может быть опасным для работы электродвигателей. В этом случае напряжение на двух фазных обмотках становиться меньше номинального в два раза.
Такой режим работы приводит к резкому снижению вращательного момента двигателя, уменьшению оборотов, увеличению потребляемого тока и, как следствие, к перегреву двигателя. На практике обычно используют устройства, отключающие трехфазную цепь при обрыве одного из линейных проводов. Режимы работы трехфазной цепи, при обрыве одного из линейных проводов, на практике могут возникнуть в результате перегорания одного из предохранителей из-за короткого замыкания какой-либо фазы.
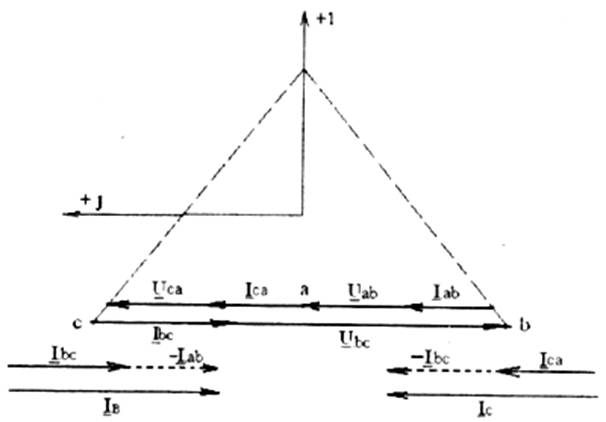
Рис. 5.11
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.До выполнения работы
1.1. Каково соотношение между фазными и линейными токами, при соединении нагрузки треугольником?
1.2.Какая нагрузка считается равномерной (симметричной), неравномерной (несимметричной)?
1.3.Покажите на схеме участки цепи, где проходят линейные и фазные токи и где действуют линейные и фазные напряжения.
2. После выполнения работы
2.1.В чем достоинства и недостатки схемы соединения треугольником по сравнению со схемой соединения звездой?
2.2. Как будут изменяться линейные токи при изменении сопротивления одной из фаз?
2.3. В каком случае применяется использование соединения потребителей треугольником?
Таблица
|
Режим нагрузки (количество ламп по фазам) (nab-nbc-nca) |
||||||||||||||||
|
Uab |
Ubc |
Uca |
IA |
IB |
IC |
Iab |
Ibc |
Ica |
Pab |
Pbc |
Pca |
Rab |
Rbc |
Rca |
Pзф |
|
|
Фазные напряжения приемников |
Линейные токи |
Фазные токи |
Активные мощности фазных приемников |
Ом |
Вт |
|||||||||||
|
В |
А |
Вт |
||||||||||||||
|
Равном. (сим.) нагрузка фаз (5-5-5) |
||||||||||||||||
|
Неравн. (несим.) нагрузка фаз (3-5-5) |
||||||||||||||||
|
Обрыв фазы «ab» (0-5-5) |
||||||||||||||||
|
Обрыв линейн. провода «А» при равном. нагрузке фаз (5-5-5) |
||||||||||||||||
Приложение к лабораторной работе № 1
Задачи для самостоятельного решения.
Задача 1.
Определить эквивалентное сопротивление всей цепи для следующих случаев:
— все выключатели (1, 2 и 3) отключены;
— Включен только выключатель 1;
— включены выключатели 1 и 2;
— включены выключатели 1 и 3;
— включены все выключатели (1, 2 и 3)
Задача 2.
Дано: U=100В; R1=4Ом; R2=6Ом; R3=2Ом; R4=8Ом; R5=15Ом.
Найти ток в резисторе R5.
Задача 3.
Дано: U=150В; R=30Ом.
Чему равны показания всех четырех амперметров?
Задача 4.
При каком положении ключа К, показание вольтметра будет больше и почему? Пояснить расчетами.
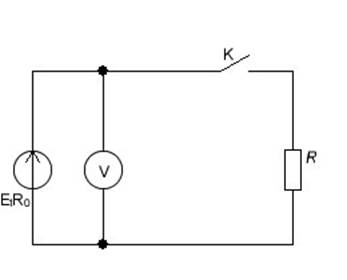
Задача 5.
Написать формулы для расчетов токов I1 и I2.
Задача 6.
Написать формулу для определения тока I1
Приложение к лабораторным работам № 2 и 3
Задачи для самостоятельного решения.
Задача 1.
Указать характер нагрузки цепи, если XL=XC=R
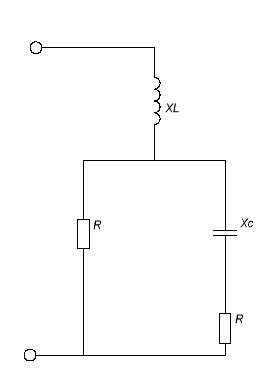
Задача 2.
По какой причине в последовательной цепи с R и C элементами, диаграмма переходит из состояния 1 в состояние 2?
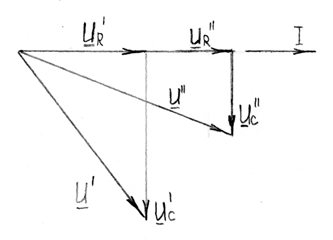
Задача 3.
Как изменится напряжение на активном сопротивлении R, если в результате изменения частоты тока f источника при неизменном напряжении U оказалось, что XL=XC?
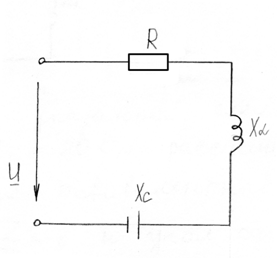
Задача 4.
Как изменится напряжение на участках R и C при замыкании ключа К, если XL=1,5XC и U останется неизменным?
Задача 5.
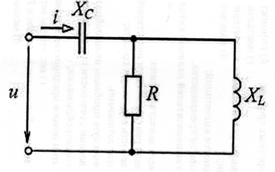
Для указанной схемы при R=XL=XC=20Ом рассчитать комплексное значение эквивалентного сопротивления цепи Zэкв и угол сдвига фаз φ между напряжением и током.
Задача 6.
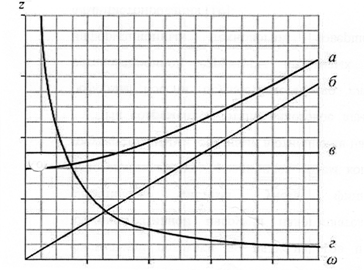
На рисунке изображены зависимости полных сопротивлений z от угловой частоты ω. Каким элементам соответствуют эти зависимости? (индуктивному, активному, емкостному)
Задача 7.
Включенные измерительные приборы показали: вольтметр – 120 В, амперметр – 12А, ваттметр – 846 Вт.
Рассчитать величину сопротивления XL, R
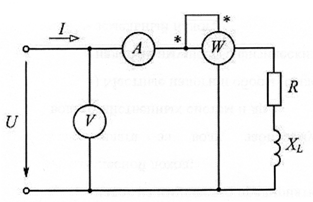
Задача 8.
При каком соотношении параметров токI на входе цепи будет опережать напряжение U?
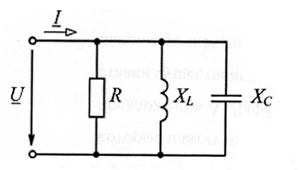
Приложение к лабораторным работам № 4 и 5
Задачи для самостоятельного решения.
Задача 1.
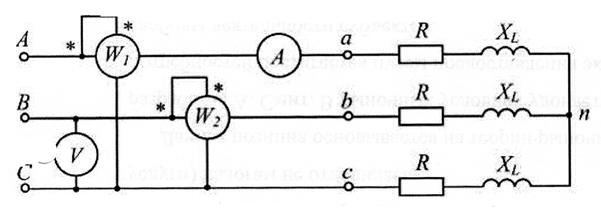
К трехпроводной трехфазной сети подключен электродвигатель, фазы которого соединены звездой. Приборы в схеме показали: U=380В, I=4.4А, PW1=653Вт, PW2=1660Вт.
Вычислить:
1. Индуктивное сопротивление XL фазы двигателя;
2. Активное сопротивление RФ фазы двигателя;
3. Комплексное сопротивление ZФ фазы двигателя;
4. Потребляемая каждой фазой активная мощность.
Задача 2.
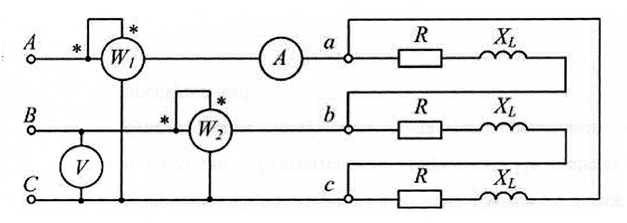
К трехпроводной трехфазной сети подключен электродвигатель, фазы которого соединены треугольником. Приборы в схеме показали: U=220В, I=7,6А, PW1=653Вт, PW2=1660Вт.
Найти:
1. Активное сопротивление RФ фазы двигателя;
2. Полное сопротивление ZФ фазы двигателя;
3. Ток Iф в каждой фазе двигателя;
4. Полною мощность трехфазной цепи.
Задача 3.
При обрыве линейного провода Aaток в каком проводе не изменится и почему?
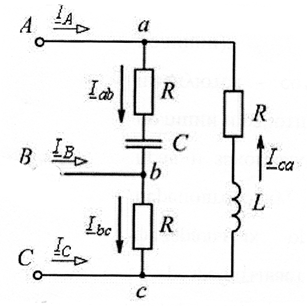
Задача 4.
Симметричный приемник с ZФ=10еj30Ом включен треугольником в трехфазную сеть с UЛ=220В. Чему равны токи в линейных проводах? Чему равна потребляемая приемником активная мощность?
Задача 5.
Определить потребляемую приемником активную мощность.
Задача 6.
Для предложенной схемы построить положения векторов токов Iab, Ibc, Ica относительно векторов фазных напряжений приемника.
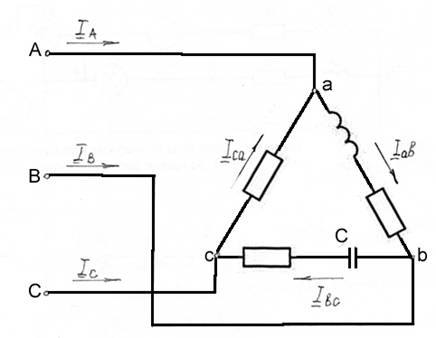
Задача 7.
В приложенной схеме при IA=3ej0 А; IB=3e-j120 А; IC=6ej120 А найти ток IN в нулевом проводе.
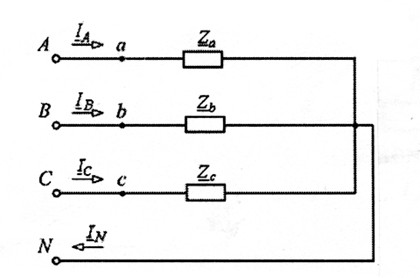
1. Алиев И. И. Справочник по электротехнике и электрооборудованию: Учеб. пособие для вузов / И. И. Алиев,-2-е изд., доп. – М.: Высш. шк., 2000. – 255 с.
2. Борисов Ю. М. и др. Электротехника: Учебник для вузов. – 2-е изд., перераб. и доп. – М.: Энергоатомиздат, 1985. – 552 с.
3. Волынский Б. Э., Зейн Е. Н. Электротехника: Учеб. пособие для вузов. – 2-е изд., перераб и доп. – М.: Энергоатомиздат, 1985. – 552 с.
4. Данилов И. А. Общая электротехника с основами электроники: Учеб. пособие / И. А. Данилов. – М.: Высш. шк., 2008. – 663 с.
5. Касаткин А. С. Курс электротехники: Учеб. пособие для вузов / А. С. Касаткин, М. В. Немцов. – 10-е изд. стер. – М.: Высш. шк., 2009. – 542 с.
6. Липатов Д. Н. Вопросы и задачи по электротехнике для программированного обучения. Учеб. пособие для студентов вузов. – Изд. 2-е, исправл. и доп., М.: Энергия, 1977. – 304 с.
ЯРУЛЛИН Ринат Бариевич
ГАЛЕЕВА Роза Абубакировна
ЭЛЕКТРОТЕХНИКА И ЭЛЕКТРОНИКА
Часть I
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
Лабораторный практикум
Издание 2-е, дополненное, переработанное
Подписано в печать 12.01.2014. Формат 60х84 1/16.
Бумага писчая. Гарнитура «Таймс».
Усл. печ. л. 4,3. Уч.-изд. л. 5. Тираж 200 экз.
Цена свободная. Заказ № 2.
Отпечатано на ризографе в редакционно-издательском отделе
Уфимского государственного университета экономики и сервиса
450078, г. Уфа, ул. Чернышевского, 145, к. 206; тел. (347) 241-69-85.