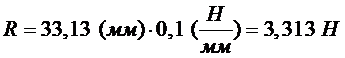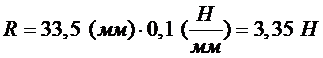Аналитический способ приведения системы сходящихся сил к простейшему виду
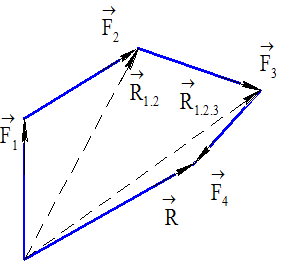
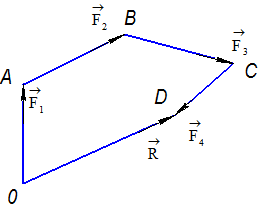
Многоугольник, сторонами которого являются векторы силы данной системы, называется силовым многоугольником (фигура OABCD рисунок 15а и 15б).
|
|
|
|
Рисунок 15а |
Рисунок 15б |
В силовом многоугольнике конец одной из сил служит началом другой.
Замыкающая сторона этого многоугольника представляет собой равнодействующую (главный вектор)![]() данной системы сходящихся сил, равную их геометрической сумме.
данной системы сходящихся сил, равную их геометрической сумме.
Необходимо обратить внимание на то, что равнодействующая сила всегда направлена от начала первого слагаемого к концу последнего слагаемого. Иными словами, стрелка равнодействующей силы всегда направлена навстречу обхода контура силового многоугольника, соответствующему последовательному сложению всех сил. Последовательность, в которой силы сходящейся системы складываются, не влияет на результат ни в случае правила параллелограмма, ни в случае построения силового многоугольника.
2.1.1Упражнения и консультации
Примечание:
Консультацией пользуйтесь в том случае, когда затрудняетесь ответить на вопросы или хотите проверить правильность своего ответа.
Задание Консультация
|
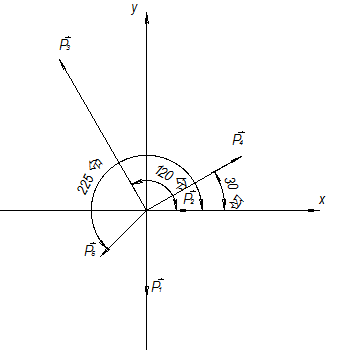
1.Задана система сходящихся сил и углы наклона сил относительно положительного направления оси Оx: Р1= 4 Н; Р2= 2 Н; Р3= 8 Н; Р4= 5 Н; Р5= 3 Н;α1= 270 о; α2= 0 о; α3= 120 о; α4= 30 о; α5= 225 о. Какими способами геометрического сложения можно определить равнодействующую силу R? Сделайте вывод о результате приведения системы сходящихся сил. Что можно сказать о линии действия равнодействующей силы? |
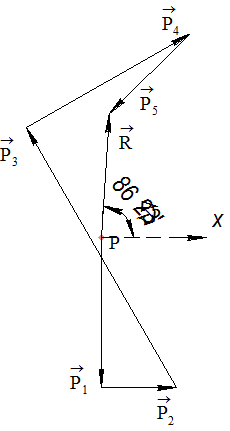
Решение: 1. Выбираем масштабный коэффициент для построения: 1Н=10мм, т. е. масштабный коэффициент при построении будет равен: ml=0,1 2. Вводим координатные оси и согласно заданию откладываем все заданные силы из начала координат (рисунок 16).
Рисунок 16 3. Равнодействующая сила определяется векторным равенством:
и ее можно определить двумя способами. 4. Определение равнодействующей силы по правилу параллелограмма. Сложим все силы, используя правило параллелограмма в следующей последовательности:
Рисунок 17
Рисунок 18
Рисунок 19
Рисунок 20 Определяем равнодействующую силу по модулю, используя формулу:
Получим:
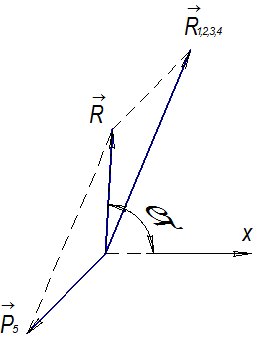
Линия действия равнодействующей силы проходит через начало координат и составляет с положительным направлением оси Ох угол φ=86,390. Модуль равнодействующей силы равен 3,313 Н. 5. Определение равнодействующей силы способом построения силового многоугольника. Строим силовой многоугольник (рисунок 21) согласно векторному равенству
Рисунок 21 Определяем равнодействующую силу по модулю, используя формулу:
Получим:
Выводы: Система сходящихся сил приводится к одной силе — равнодействующей. Для определения направления равнодействующей силы измеряем угол между линией действия равнодействующей силы и положительным направлением оси Ох. Линия действия равнодействующей силы проходит через начало координат и составляет с положительным направлением оси Ох уголφ=86,230 Определяем относительную ошибку при определении модуля равнодействующей силы двумя графическими методами:
|
2.2Аналитический способ приведения системы сходящихся сил к простейшему виду (аналитическое определение равнодействующей силы).
Многие задачи статики решаются аналитическим методом, при котором используются не сами силы, а их проекции на оси координат.
Каждая из сил, геометрическая сумма которых дает равнодействующую силу, может быть представлена через ее проекции на координатные оси и единичные векторы (орты):
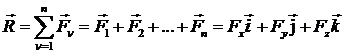 (4)
(4)
Определение равнодействующей системы сходящихся сил аналитическим способом проводится в следующей последовательности:
— выбираются оси координат;
— записывается векторное выражение равнодействующей силы;
— определяются проекции всех заданных векторов на координатные оси;
— по известным проекциям на координатные оси определяется модуль вектора;
— направление вектора определяется по направляющим косинусам.
Пример 1
Пусть задана плоская система сходящихся сил (рисунок 22).Равнодействующая этих сил определяется выражением:
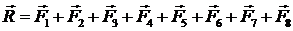 (5)
(5)
Поместим начало прямоугольной системы координат в точку пересечения линий действия сил.
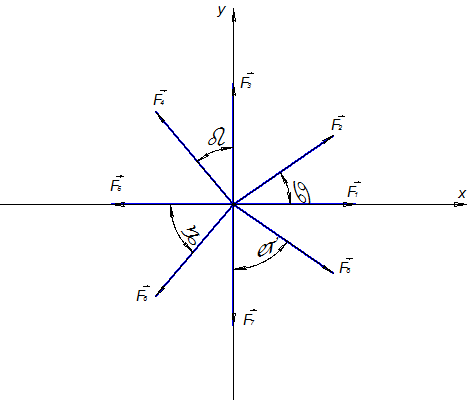
Рисунок 22
Каждую из сил можно задать ее проекциями на две перпендикулярные оси координат Ох и Оу, учитывая, что проекция геометрической суммы векторов на какую-нибудь ось равна алгебраической сумме проекций составляющих векторов на ту же ось.
При решении задач удобнее вычислять абсолютное значение проекции силы как произведение модуля силы на косинус (синус) острого угла между линией действия силы и осью, определяя знак проекции непосредственно по чертежу.
Проектируя векторное равенство (5) на оси координат получим:
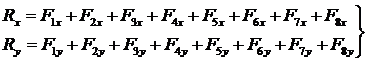 (6)
(6)
где Fkx, Fky – проекции сил на координатные оси, а Rx, Ry – проекции равнодействующей силы на те же координатные оси.
Проекции каждой силы на оси координат Ох и Оу соответственно равны:
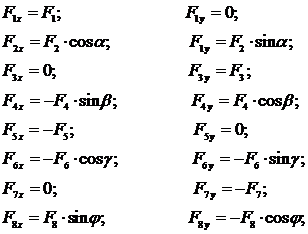 (7)
(7)
Так как составляющие равнодействующей системы сил Rx, Ry взаимно перпендикулярны, то модуль равнодействующей силы определяется через проекции составляющих сил на координатные оси по формуле:
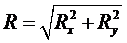 ; (8)
; (8)
Направление силы определяется по направляющим косинусам:
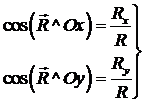 ; (9)
; (9)
Эти выводы справедливы как для плоской, так и для пространственной системы сходящихся сил.
Для пространственной системы сходящихся сил, соответственно, получим:
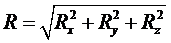 (10)
(10)