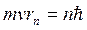Боровская теория атома

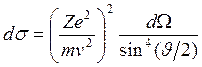– формула Резерфорда.

Экспериментальная проверка полученной зависимости основана на следующих соображениях.

Если акты рассеяния независимы, т. е. происходят на разных атомах, число атомов-рассеивателей в единице объема мишени, объем, в котором происходит рассеяние, то число частиц, рассеянных в единицу времени в телесный угол , можно найти, используя формулу Резерфорда

.

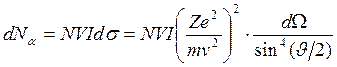Отсюда следует, что для заданного элемента телесного угла 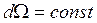должно выполняться условие

,

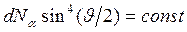что и было получено в эксперименте.

Этот результат дал опытное обоснование модели атома Резерфорда. Однако эта модель противоречила представлениям классической физики:

1.  Если заряды неподвижны, то такая система неустойчива (теорема Ирншоу). Поэтому Резерфорду пришлось отказаться от статической модели атома.

2.  Если заряды движутся по искривленным орбитам, то тратится энергия на излучение при ускоренном движении и электроны должны в итоге упасть на ядро.

2.Спектры атомов.

Важный вклад в развитие представлений о структуре атомов внесли оптические исследования.

Из опыта известно, что накаленные твердые тела имеют сплошные спектры излучения. У газов же, наряду со сплошными спектрами, наблюдались линейчатые и полосатые спектры. К 1900 г. было, в основном, выяснено, что полосатые спектры соответствуют излучению молекул, а линейчатые – атомов и ионов.

Более того, оказалось, что в атомных спектрах линии располагаются не хаотически, а подчиняются некоторой закономерности.

Наилучшим образом эти закономерности прослеживались в спектре атома водорода (и до некоторой степени у щелочных металлов), который измерил А. Ангстрем (1863 г.). В 1885 г. Бальмер установил аналитическую зависимость распределения излучения по длинам волн в спектре атома водорода.

,

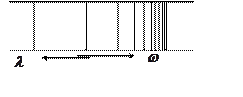
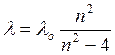или, переходя к частотам, ()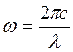

,

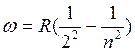где — постоянная Ридберга (1890 г.), 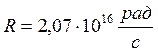, — целое число: 3, 4, 5,…

Если переписать выражение в виде

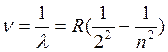, то .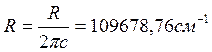

Здесь в согласии с принятой в спектроскопии традицией обозначает волновое число, т. е. число длин

волны, укладывающихся в одном сантиметре.

При изучении спектров излучения атомов было найдено, что спектральные линии могут быть объединены в группы, названные сериями. В пределах каждой серии положение линии подчиняется общей закономерности, которая носит название обобщенной формулы Бальмера .

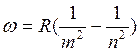, где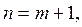

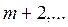
Спектральные группы линий получили названия по именам исследователей:

— серия Лаймана (1916 г.) – ультрафиолетовые лучи;

— серия Бальмера (1885 г.) – видимый свет;

— серия Пашена (1908 г., предсказал Ритц) – инфракрасные лучи;

— серия Брэккета (1922 г.) – инфракрасные лучи;

— серия Пфунда (1924 г.) – инфракрасные лучи;

…………………………………………………………………………………

Наблюдаемые спектральные закономерности не укладывались в рамки классической теории, согласно которой параметры орбиты и угловая скорость движения по ней электрона могут принимать любые значения и как следствие обусловливать непрерывные спектры излучения атомов.

3.Боровская теория атома.

Выход из создавшегося тупика был найден Н. Бором в 1913 г., ценой введения предположений, противоречащих классическим представлениям.

Постулаты Бора.

А) Существование стационарных состояний атома.

Электроны движутся в атоме по определенным стационарным орбитам, которые удовлетворяют определенным квантовым условиям. Электрон, находясь на этих орбитах не излучает. Энергия атома может принимать только дискретные значения

Б) Правило частот Бора.

При переходе из одного стационарного состояния в другое атомы испускают или поглощают излучение строго определенной частоты: .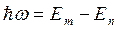

Условие квантования.

Для одномерного движения: 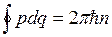, 2, 3,…

— обобщенный импульс; обобщенная координата.

Круговая орбита – пример одномерного движения, при котором в качестве обобщенной координаты выступает угол, т. е. а роль обобщенного импульса играет момент количества движения

,

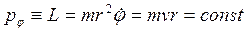который сохраняется, поскольку движение происходит в центральном поле. Тогда

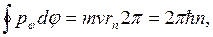или .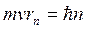

Дополнив условие квантования основным уравнением динамики, описывающим движение электрона в электростатическом поле заряда ядра , получим систему уравнений для определения радиуса электронной орбиты :