Цепь переменного тока с активным и индуктивным сопротивлениями

Из сказанного можно сделать вывод, что емкостное сопротивление обратно пропорционально емкости.

Таким образом. емкостное сопротивление:

где Хс — емкостное сопротивление, ом;

ώ — угловая частота переменного тока, рад/сек;

С —емкость, ф.

Известно, что угловая частота . Поэтому емкостное сопротивление можно определить так:

где f— частота переменного тока, гц.

Если включенная емкость измеряется в микрофарадах, то ем­костное сопротивление

Если емкость измеряется в пикофарадах, то

Следует подчеркнуть, что имеется существенное различие меж­ду емкостным и активным сопротивлениями. Как известно, актив­ная нагрузка безвозвратно потребляет энергию генератора пере­менного тока.

Если же к источнику переменного тока присоединена емкость, то, как было рассмотрено выше, энергия генератора расходуется при заряде конденсатора на создание электрического поля между пластинами и возвращается обратно генератору при разряде кон­денсатора.

Следовательно, емкостная нагрузка не потребляет энергию ге­нератора, а в цепи с емкостью происходит «перекачивание» энергии из генератора в конденсатор и обратно. По этой причине емкостное сопротивление, как и индуктивное, называется реактивным.

Пример. Конденсатор емкостью С=2 мкф включен в цепь переменного тока, частота которого 50 гц. Определить:

1)  его емкостное сопротивление при частоте f=50 гц;

2)  емкостное сопротивление этого конденсатора переменному току, частота которого 500 гц.

Решение. Емкостное сопротивление конденсатора переменному току при частоте f=50 гц

При частоте f=500 гц

 Из приведенного примера видно, что емкостное сопротивление конденсатора уменьшается с повышением частоты, а с уменьшением частоты переменного тока емкостное сопротивление возрастает. Для постоянного тока, когда напряжение на зажимах цепи не изме­няется, конденсатор практически обладает бесконечно большим со­противлением и поэтому он постоянного тока не пропускает.

§ 55. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С АКТИВНЫМ И ИНДУКТИВНЫМ СОПРОТИВЛЕНИЯМИ

Любая проволочная катушка, включенная в цепь переменного тока, обладает активным сопротивлением, зависящим от материала, Длины и сечения проволоки  ,  и индуктивным сопротивлением, которое зависит от  индуктивности катушки и частоты переменного тока, протекающего по ней (ХL=ωL=2πfL). Такую катушку можно рассматривать как приемник энергии, в котором активное и индуктивное сопротивления соединены последовательно.

Рассмотрим цепь переменного тока, в которую включена катуш­ка индуктивности (рис. 56, а) с активным r и индуктивным ХL со­противлением. Падение напряжения на  активном сопротивлении

Падение напряжения на индуктивном сопротивлении

Построим векторную диаграмму тока и напряжения (рис. 56, б) для рассматриваемой цепи.

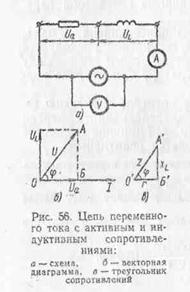
Отложим по горизонтали вектор тока  I в выбранном масштабе. Известно, что ток  и напряжение в цепи с активным сопротивлением совпадают по фазе, поэтому  вектор падения напряжения на активном сопротивлении откладываем по вектору  тока.

В цепи с индуктивностью ток отстает от напряжения на угол =90°.  Поэтому вектор падения напряжения на индуктивном сопротивлении откладываем на диаграмме вверх под углом 90° к  вектору тока.

Для определения общего напряжения, приложенного к цепи, сложим векторы  Ua. и UL Суммой этих векторов будет диагональ параллелограмма — вектор  U. Треугольник АОБ, стороны которого  выражают соответственно напряжения Uа, UL и общее напряжение и, называется треугольником напряжений. На основании теоремы Пифагора — в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов — следует, что общее напряжение на зажимах цепи

Пример. Падение напряжения на активном сопротивлении Ua=15в. Напря­жение  на индуктивном сопротивлении UL=26 в. Вычислить общее напряжение, приложенное к цепи.

Решение. Общее напряжение на зажимах цепи переменного тока с после­довательно соединенными активным и индуктивным сопротивлениями.

Чтобы определить полное сопротивление цепи переменного тока с активным и индуктивным сопротивлениями, следует разделить векторы Ua=Ir и UL =IXL на число I, выражающее силу тока в цепи, и построить треугольник А’О’В’ (рис. 56, в), стороны которого меньше сторон треугольника напряжений в I раз. Образованный треугольник называется треугольником сопротивлений. Его сторо­нами являются сопротивления r и ХL и полное сопротивление цепи Z.

Пользуясь теоремой Пифагора, можно написать что,

отсюда полное сопротивление цепи

Пример. Активное сопротивление катушки r=7 ом, а ее индуктивное сопро­тивление ХL=24 ом. Вычислить полное сопротивление катушки.

Решение. Полное сопротивление катушки переменному току

Сила тока в цепи с  активным и  индуктивным сопротивлениями определяется по закону Ома:

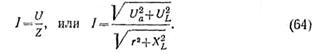
На векторной диаграмме видно, что в цепи переменного тока с активным и индуктивным сопротивлениями ток и напряжение не совпадают по фазе. Ток отстает от напряжения — на угол .

Угол сдвига между током и напряжением можно определить, если известен косинус этого угла.

Из треугольника напряжений косинус угла сдвига фаз

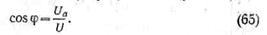
Теперь можно, пользуясь таблицей тригонометрических функ­ций, определить угол .

Пример. Падение напряжения на активном сопротивлении катушки Ua =30 в. Общее напряжение на ее зажимах U=60в. Определить угол сдвига фаз между током и напряжением в цепи.

Решение. На основании данных найдем

По таблице тригонометрических функций угол сдвига фаз при со =0,5 составляет 60°.