Чему равна длина волны амплитуды вероятности электрона
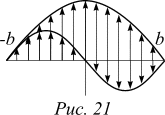 Распределение амплитуд должно удовлетворять требованию: в точках x=±b/2 амплитуда должна обращаться в ноль. Формула (4) допускает такую возможность, но не при любом значении k. Волновое число должно принимать только значения —
Распределение амплитуд должно удовлетворять требованию: в точках x=±b/2 амплитуда должна обращаться в ноль. Формула (4) допускает такую возможность, но не при любом значении k. Волновое число должно принимать только значения — ![]() (5)
(5)
Заметим, требованию равенства нулю амплитуды вероятности на границах ямы может удовлетворять не только функция (4), но и
y(x)=2y0sinkx (6)
при следующих значениях волнового числа: ![]() (7)
(7)
Итак, можно сделать вывод, что распределение амплитуд вероятности частицы в бесконечно глубокой потенциальной яме описывается либо законом синуса, либо законом косинуса. Объединение ограничений (5) и (7), налагаемых на волновое число, дает![]() (8)
(8)
Из условия (8) вытекает важное следствие: модуль импульса частицы p=ћk также может принимать только дискретный ряд значений:![]() (9)
(9)
где n принимает только целые значения: 1, 2, 3,… Полная энергия частицы E равна кинетической энергии, поэтому
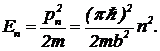 (10) Это энергетический спектр частицы. Выражение (10) показывает, что
(10) Это энергетический спектр частицы. Выражение (10) показывает, что 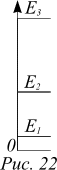 энергия частицы в потенциальной яме квантуется. Квантованный энергетический спектр называют дискретным.
энергия частицы в потенциальной яме квантуется. Квантованный энергетический спектр называют дискретным.
Зависимость от времени амплитуды вероятности частицы находиться в состоянии с определенным значением энергии сводится к вращению стрелок, изображающих амплитуды. Так что, глядя на рисунок 21 с примером распределения амплитуд, надо иметь в виду, что все стрелки и весь график распределения амплитуд вращаются. При этом модули амплитуд не изменяются во времени. Из этого следует, что вероятность застать частицу в состоянии с определенной энергией не изменяется со временем.
Вопрос 1. Пусть частица в яме находится в состоянии с определенным значением энергии. В этом случае, в соответствии с (10), можно считать, что p2 также имеет определенное значение — неопределенность значения импульса равна нулю. Но при этом неопределенность координаты не превышает b. Кажется, что возникает противоречие принципу неопределенности. На самом деле никакого противоречия нет. В чем ошибка рассуждений?
Задача 5. Частица массы m находится в бесконечно глубокой прямоугольной потенциальной яме ширины b в стационарном состоянии на энергетическом уровне №n. Найдите силу, с которой частица при этом давит на стенки ямы.
Решение. Сила направлена в сторону убывания энергии и равна минус производной от энергии по координате стенки ямы:
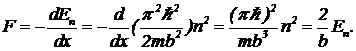 (11)
(11)
Сила давления растет с ростом номера уровня.
Задача 6. Частица массы m находится в прямоугольной потенциальной яме ширины b. Глубина потенциальной ямы равна U0. Какое число стационарных связанных состояний у частицы?
3.2 Обобщение
Строгая квантовая теория показывает, что частицы, находящиеся в ограниченной области пространства, всегда имеют дискретный энергетический спектр. Строгий расчет дает, что энергетический спектр электрона в атоме водорода точно такой же, какой дает теория Бора.
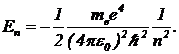 (12)
(12)
Атомные спектры также являются дискретными, так как электроны в атомах движутся в ограниченной области пространства.
Другой пример — спектр энергий гармонического осциллятора — 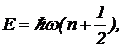 (13)
(13)
где w — собственная частота колебаний осциллятора, n=0, 1, 2, …
Гармонический осциллятор — чрезвычайно распространенная в природе физическая система. В курсе 9 класса показано, что несколько упруго связанных между собой осцилляторов ведут себя как ряд невзаимодействующих гармонических осцилляторов — мод, каждая из которых движется, как одномерный гармонический осциллятор. Например, натянутая с силой F струна, длины L и линейной плотностью r имеет целый ряд собственных частот, которые задаются формулой —
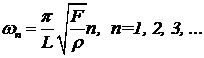 (14)
(14)
Она может колебаться с одной из этих частот (в одной моде). При этом струна имеет конфигурацию стоячей волны (моды струны — стоячие волны). Согласно квантовой механике, энергетический спектр струны представляет собой наложение спектров вида (13) всех мод.
Стоячие электромагнитные волны — тоже гармонические осцилляторы. Переходы стоячих волн на высшие уровни рассматриваются как рождение новых фотонов.
4. Домашнее задание
4.1 Теоретический материал
Проработать материал занятия по пособию, по своим конспектам и по учебнику “Физика 11” под ред. А. А.Пинского. §72. Сделать доклад “Частица в бесконечно глубокой потенциальной яме”
4.2 Решение задач
Задача 1. Волна амплитуды вероятности частицы в трехмерном потенциальном ящике размером Lx´Ly´Lz имеет волновой вектор с компонентами kx, ky, kz. Задача об описании состояний частицы в таком ящике распадается на три независимые одномерные задачи, решенные на настоящем занятии.
а) Найдите разрешенные значения проекций волнового вектора частицы.
б) Как выглядит энергетический спектр частицы?
в) В ящике находится N частиц. Полагая, что в состоянии теплового равновесия средние значения квадратов проекций волновых чисел равны между собой, определите давление частиц на стенки ящика. Выразите давление через среднее значение энергии одной частицы.
занятие 2.1.11
самостоятельная работа
2. Самостоятельная работа
Задача 1. Чему равна длина волны амплитуды вероятности электрона, с кинетической энергией 0,512 МэВ?
Задача 2. Если I0 — интенсивность поляризованного света, то интенсивность света, прошедшего через поляризатор с осью пропускания, повернутой под углом J к плоскости поляризации, равна I=I0cos2J (закон Малюса). Свет не проходит сквозь скрещенные поляризаторы (поляризаторы скрещены, если угол между осями пропускания составляет 900).
а) Чему равна амплитуда того, что поляризованный фотон пройдет через поляризатор с осью пропускания, ориентированной под углом J к плоскости поляризации фотона? Какая доля света поглощается?
б) Между двумя скрещенными поляризаторами поставили третий, ось пропускания которого составляет угол J с осью пропускания первого. Чему равна интенсивность света, прошедшего через систему трех поляризаторов, если интенсивность света, вышедшего из первого, равна I0?
в) Средний поляризатор повернули на 90о. Как изменится амплитуда прохождения фотона через него? Чему равны полные амплитуды прохождения при обеих установках среднего поляроида?
г) Поляризатор часть света поглощает. Почему же добавление в середину системы поляризатора увеличивает интенсивность света, прошедшего через систему? Опишите явление прохождения одного фотона на языке амплитуд вероятности.
Задача 3. Через три щели, расположенные на равных расстояниях b друг от друга, ширина каждой из которых меньше длины волны l, пропускают пучок электронов. Электроны попадают на экран, расположенный на расстоянии L от щелей. Амплитуды попадания электрона в каждую из щелей одинаковы. Рассмотрите ситуацию L>>l, b, x.
а) Определите частоту срабатывания детектора I, закрепленного на экране на расстоянии x от начала координат. Считайте, что частота срабатывания детектора, установленного в начале координат, равна I0. Полагайте также, что модуль амплитуды попадания электрона из щели на экран не зависит от x.
б) Получите приближенное выражение расстояния между центральным и первым максимумом интенсивности попадания электронов.
Задача 4. Оцените вращательную энергию основного состояния молекулы водорода. Выразите ее через момент инерции молекулы и постоянную Планка.
Задача 5. Частица массы m с импульсом p падает на потенциальную ступеньку высоты 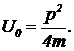 Как относятся частоты изменения амплитуды вероятности по обе стороны ступеньки, если частица находится в стационарном состоянии? Как относятся значения длины волны амплитуды вероятности по обе стороны ступеньки в стационарном состоянии?
Как относятся частоты изменения амплитуды вероятности по обе стороны ступеньки, если частица находится в стационарном состоянии? Как относятся значения длины волны амплитуды вероятности по обе стороны ступеньки в стационарном состоянии?
Задача 6. Волна амплитуды вероятности частицы в трехмерном потенциальном ящике размером Lx´Ly´Lz имеет волновой вектор с компонентами kx, ky, kz. Задача об описании состояний частицы в таком ящике распадается на три независимые одномерные задачи, решенные на занятии 2.1.10.
а) Найдите возможные значения проекций волнового вектора частицы.
б) Как выглядит энергетический спектр частицы?
в) В ящике находится N частиц. Полагая, что в состоянии теплового равновесия средние значения квадратов проекций волновых чисел равны между собой, определите давление частиц на стенки ящика. Выразите давление через среднее значение энергии одной частицы.


