Закон Ома в интегральной форме для элементарного участка

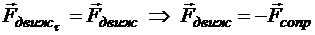
В наиболее распространённых случаях сила сопротивления пропорциональна скорости. Коэффициент пропорциональности запишем в виде , где r — характеристика проводящей среды, называемая удельным сопротивлением.

.

Подставляя во II-й закон Ньютона

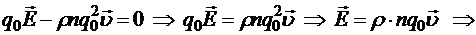
Þ

Þ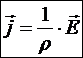

Это и есть закон Ома в дифференциальной форме:

внутри проводника стационарное векторное поле напряжённости порождает векторное поле плотности тока.

Ещё раз подчеркнём, что закон Ома приложим к средам, в которых сила сопротивления, действующая на носитель, пропорциональна его дрейфовой скорости.

§17.3. Закон Ома в интегральной форме для элементарного участка

Дальше будем исходить из предположения об однородности удельного сопротивления r и напряжённости поля движущих сил на поперечном сечении проводника (из однородности следует однородность ).

Пусть S — произвольное поперечное сечение цепи (из определения поперечного сечения следует, что параллельно ).

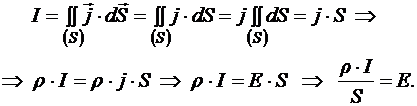
Умножим последнее равенство на элементарное перемещение dl вдоль вектора плотности тока, а значит, параллельное вектору :

.

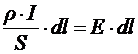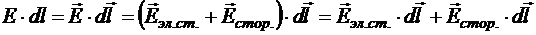
Первое слагаемое правой части — элементарный сброс потенциала электростатического поля. Второе слагаемое 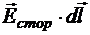— элементарная работа сторонних сил на перемещении единичного положительного заряда. Эту величину принято называть элементарной электродвижущей силой (ЭДС) и обозначать de. Тогда имеем:

.

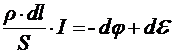Множитель

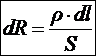
характеризует элементарный участок цепи постоянного тока dl независимо от силы тока, сброса потенциала и работы сторонних сил и называется элементарным сопротивлением. С учётом этого обозначения получаем интегральный закон Ома для элементарного участка цепи постоянного тока:

.

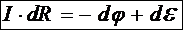Интегральность последнего соотношения связана с тем, что рассматривается всё поперечное сечение, а не одна его точка.

§17.4. Закон Ома для неоднородного участка цепи (II-я форма интегрального закона Ома)

Проинтегрировав это соотношение на конечном участке цепи постоянного тока между поперечными сечениями S1 и S2, получим интегральный закон Ома для участка цепи постоянного тока:

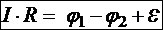
Здесь 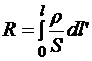называется сопротивлением участка. Если участок сделан из одного материала, имеет одинаковую температуру и поперечное сечение, то сопротивление участка выражается привычным со школы образом:

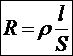
Участок цепи, содержащий источник ЭДС, называется неоднородным. Закон Ома для этого участка соотносит между собой три величины, каждая из которых связана с работой сил определённого класса.

·  — работа сторонних сил на перемещении единичного положительного заряда по данному участку цепи (от сечения S1 до сечения S2); эту величину называют электродвижущей силой (ЭДС) участка;

·  — работа электростатических сил на перемещении единичного положительного заряда по данному участку цепи; эту величину, как и в электростатике, мы будем называть напряжением участка и обозначать буквой U;

·  — абсолютная величина работы сил сопротивления на перемещении единичного положительного заряда по данному участку цепи; эту величину мы будем называть падением напряжения участка.

По определению падение напряжения всегда положительно и равно количеству тепла Q+1, выделившемуся на участке при протекании по нему единичного положительного заряда. ЭДС и напряжение могут быть как положительными, так и отрицательными (очевидно, что запрещён случай, когда обе эти величины отрицательны). Необходимо твёрдо помнить, что напряжение – это разность потенциалов между входным поперечным сечением участка и выходным. Поскольку при постоянном токе дрейфовая скорость единичного положительного заряда от сечения к сечению не меняется, то напряжение U является сбросом механической энергии единичного положительного заряда:

.

Следовательно, закон Ома для неоднородного участка цепи можно переписать так:

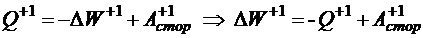
Отсюда ясно, что

интегральный закон Ома участка цепи представляет собой закон изменения механической энергии единичного положительного заряда на этом участке.

Электрическая схема неоднородного участка имеет следующий вид в случае положительной работы сторонних сил:

Рис.17.2

Для того чтобы записать интегральный закон Ома для данного неоднородного участка, на схеме необходимо показать направление протекания тока (направления вектора плотности тока), силу тока и потенциалы на входе и выходе участка. Две характеристики неоднородного участка: ЭДС и сопротивление, имеют свои схемотехнические обозначения. При этом символ ЭДС специально выбран так, чтобы показать полярность по отношению к направлению протекания тока. Обратим внимание, что на схеме участка символ «e» всегда обозначает абсолютную величину. Знак работы сторонних сил определяется по следующему правилу: если ток «втекает» в короткую черту, а «вытекает» из длинной, то сторонние силы совершают положительную работу. Если же наоборот, то сторонние силы совершают отрицательную работу. Значит, на последней приведённой схеме ЭДС включена положительно. Схема неоднородного участка с отрицательно включённой ЭДС будет иметь следующий вид:

Рис.17.3

Участок с положительно включённой ЭДС называется участком источника. Участок с отрицательно включённой ЭДС называется участком потребителя. На участке источника источник ЭДС отдаёт свою энергию носителям заряда, на участке потребителя источник ЭДС отбирает энергию у носителей заряда. В частности, если источник ЭДС — аккумулятор, то при отрицательном включении происходит его зарядка. В дальнейшем в записи интегрального закона Ома для неоднородного участка цепи мы будем в явном виде писать знак ЭДС, то есть будем записывать закон не в алгебраическом, а в арифметическом виде: