Поток вектора через поверхность

Рассмотрим (рис.13.5) элементарную поверхность , находящуюся в той же точке пространства, что и поверхность сферы радиуса r, и видимую под тем же телесным углом dW из точки О:

Рис.13.5

Очевидно, что орт нормали к поверхности dSсф (обозначим его ) можно определить так:

.

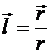Из-за малости угла dW все радиальные линии, пересекающие dSсф и dS считаются параллельными вектору и, следовательно, перпендикулярными dSсф. Это означает, что величина dSсф представляет собой проекцию вектора на направление радиального орта , то есть

,

следовательно,

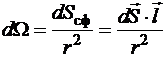
§13.3. Поток вектора через поверхность

Пусть точке пространства, в которой находится элементарная поверхность , соответствует вектор поля . Тогда по определению можно ввести понятие элементарного потока векторного поля через поверхность:

Интеграл элементарных потоков по поверхности S, погружённой в векторное поле , по определению называется потоком вектора через поверхность S:

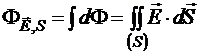
§13.4. Теорема ОГ

Если − напряжённость поля точечного заряда Q, то в точке пространства, отстоящей от источника на вектор ,

,

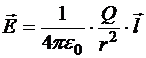где 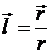. Тогда элементарный поток через поверхность , находящуюся в этой точке и направленную от заряда, имеет вид:

.

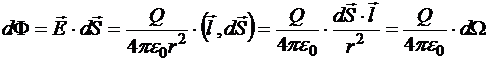Понятно, что dW − телесный угол, под которым видна поверхность из точки расположения источника. Отметим, что выражение потока напряжённости через телесный угол оказалось возможным исключительно благодаря обратной квадратичной зависимости напряжённости поля точечного источника от расстояния.

Подсчёт потока напряжённости поля точечного заряда через замкнутую поверхность S рассмотрим в двух случаях.

а) Заряд находится внутри поверхности S

Рис.13.6

Из рисунка 13.6 видно, что интегрирование в этом случае производится по полному телесному углу.

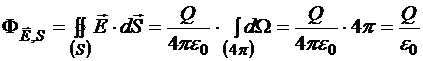
б) Заряд находится вне поверхности S

Рис.13.7

Под телесным углом DW (рис.13.7) из точки Q видны две поверхности, образующие замкнутую поверхность S: S1, нормали которой обращены к заряду, и S2, нормали которой обращены от него.

.

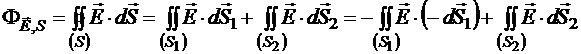Теперь в первом интеграле интегрирование производится по поверхности, нормали которой тоже обращены от источника, следовательно, теперь оба слагаемых могут быть выражены через телесный угол DW:

;

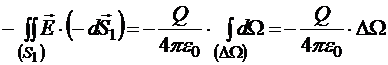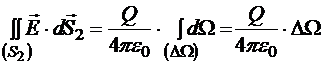
Тогда понятно, что полный поток через поверхность S равен 0.

Если имеется совокупность точечных зарядов, то в соответствии с принципом суперпозиции полей

,

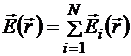где N − количество точечных источников. Следовательно, поток напряжённости их общего поля через произвольную замкнутую поверхность S:

,

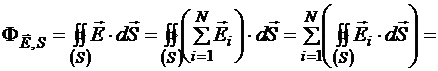
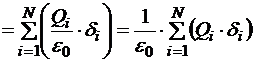где di=1, если Qi находится внутри замкнутой поверхности и di=0, если Qi находится за пределами замкнутой поверхности, следовательно, 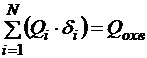− заряд, охваченный замкнутой поверхностью. Тогда окончательно:

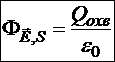
Поток напряжённости электрического поля через произвольную замкнутую поверхность в вакууме равен заряду, охватываемому этой поверхностью, делённому на электрическую постоянную вакуума.

§13.5. Применение теоремы ОГ

Теорема даёт возможность рассчитать электрическую напряжённость поля распределённого заряда в случаях простых, но важных пространственных конфигураций.

13.5.1. Напряжённость поля равномерно заряженной сферы

Рис.13.8

Равномерность заряда сферы означает, что её поверхностная плотность заряда одинакова во всех точках сферы:

,

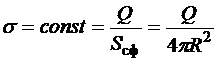где R − радиус сферы, а Q − её заряд (для простоты будем считать, что он положителен).

Сначала рассмотрим произвольную точку А внутри сферы заряда.

Рис.13.9

Рассмотрим два вертикальных малых телесных угла dW, под которыми из точки А видно два участка поверхности сферы заряда dS1 и dS2 (рис.13.9). Из рассмотренной выше связи площади и телесного угла, под которым она видна, следует:

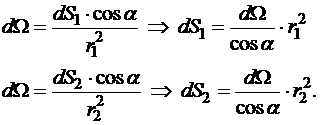
С каждой из этих элементарных поверхностей связан элементарный заряд

соответственно. Силы, действующие со стороны этих зарядов на пробный заряд q>0, помещённый в точку А (рис.13.10), в соответствие с законом Кулона равны по модулю:

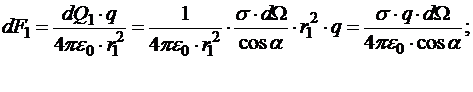
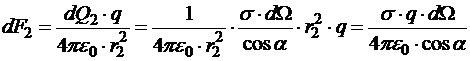
и противоположны по направлению.

Рис.13.10

Следовательно, полная сила, действующая со стороны поверхности сферы заряда на пробный заряд q и связанная с интегрированием по полному телесному углу, будет равна 0. А поскольку, 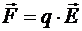, то из равенства 0 силы следует равенство 0 напряжённости в любой точке внутри сферы.