ВУЗы по физике
Готовые работы по физике
Как писать работы по физике
Примеры решения задач по физике
Решить задачу по физике онлайнПринцип суперпозиции полей в применении к потенциалу
Есть ещё одно более краткое обозначение, подчёркивающее векторный характер оператора. Это символ 
, называемый вектором набла. С его помощью операция взятия градиента скалярного поля 
обозначается как произведение вектора набла на скаляр j: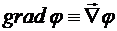 
.
Итак, мы можем записать:
.
Из собственного опыта мы знем, что физический смысл градиента достаточно труден для понимания. Поэтому нелишне будет воспроизвести здесь страницу из учебника математики и обсудить её.
Выберем в пространстве, натянутом на декартовы координаты, произвольное направление, задаваемое ортом 
, и введём координату по этому направлению L (рис.14.3).
Рис.14.3
Если мы не будем сходить с оси L, то скалярная функция положения будет зависеть только от координаты L:
Из рисунка легко сообразить, что
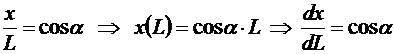
Аналогично:
; 
.
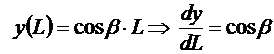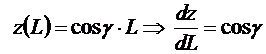Теперь найдем производную трёхмерной скалярной функции по направлению , то есть 
. По правилу дифференцирования сложной функции
.
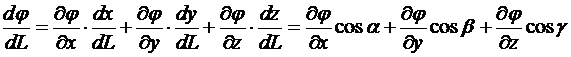Но проекция орта на направление 
определяется так: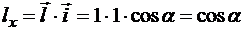 
, то есть
Тогда производная по направлению принимает вид:
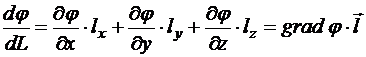
Итак, пространственная быстрота изменения скалярной функции от положения 
в направлении равна скалярному произведению градиента j на орт направления. Значит, есть такие направления, вдоль по которым j в данной точке пространства не меняется, то есть =0, следовательно,
.
Совокупность таких направлений в данной точке пространства образует поверхность 
Рис.14.4
С другой стороны, направление (рис.14.4) будет параллельно градиенту j, следовательно, вдоль по этому направлению быстрота пространственного изменения функции j будет максимальна и её абсолютная величина будет, как раз, равна модулю градиента. Отсюда «понятное» определение: градиент функции от пространства j в данной точке − это вектор максимальной пространственной быстроты изменения функции в этой точке. Тогда для напряжённости электростатического поля можно дать такое утверждение: вектор 
в данной точке пространства есть вектор максимальной пространственной скорости убывания потенциала в этой точке. Отсюда, кстати, проистекает наиболее часто применяемая размерность напряжённости: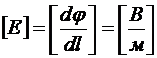 
.
Как следует из сказанного, поверхность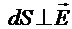 
в данной точке пространства — это поверхность, вдоль по которой потенциал не изменяется. Такая поверхность называется эквипотенциальной. Картина силовых линий − не единственный способ представления потенциального поля. Его можно представить совокупностью эквипотенциальных поверхностей, соответствующих значениям потенциала, отстоящих друг от друга на одинаковый (произвольно выбранный) сдвиг Dj:
|
Рис.14.5
Левый рисунок соответствует однородному полю, а правый − центральному полю точечного источника.
§14.4. Принцип суперпозиции полей в применении к потенциалу
Вспомним формулу выражения потенциала через напряжённость:
.
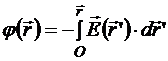Т. к. физический смысл имеет только разность потенциальных энергий, то это верно и в отношении потенциала. Поэтому выбирать точку начала отсчёта потенциала можно в любом месте. Если начало отсчёта потенциала поля каждого источника поместить в одну точку пространства О, то с учётом принципа суперпозиции для напряжённости:
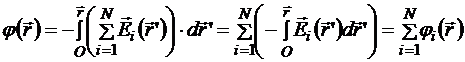
Перепишем кратко:
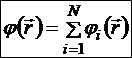
§14.5. Примеры расчёта потенциалов полей разных конфигураций
При ограниченном распределении источников поля в пространстве значительное упрощение математических выражений потенциала достигается, если ноль потенциала выбирать на бесконечном удалении от области расположения источников. При вычислении контурных интегралов
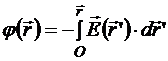
во всех приводимых примерах мы будем двигаться по силовой линии поля, то есть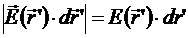 
.
14.5.1. Точечный заряд
Начало положения выбираем в точке положения источника поля.
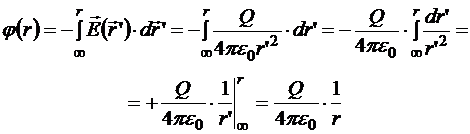
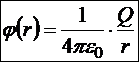
Несколько точечных источников всегда находятся в ограниченной области пространства, следовательно, можно удалиться на бесконечно большое расстояние от всех источников сразу. И эта точка, естественно, будет общим началом отсчёта потенциалов всех источников. Тогда по принципу суперпозиции потенциал общего поля в произвольной точке А
,
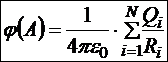где Ri — расстояние от точечного заряда Qi до точки А.
14.5.2. Равномерно заряженная сфера
Приведём (рис.14.6) график зависимости модуля напряженности от расстояния до центра сферы для сферы радиуса R с положительным зарядом Q (по материалам предыдущей главы).
Рис.14.6
Поскольку за пределами сферы поле не отличатся от поля точечного заряда, то и интегрирование от бесконечности до любой точки проходит точно также. Следовательно, в этой области пространства потенциал совпадает с потенциалом поля точечного заряда.
Рассмотрим произвольную точку внутри сферы (r<R). Контур интегрирования − радиальную линию, проходящую через избранную точку, разобьём на два участка: от бесконечности до R и от R до r. Тогда полный интеграл распадётся на два:
МГМИМО
Скидка 30% по промокоду Diplom2020
Получи промокод на скидку 20%
Дипломные