Цикл ренкина в pv и ts координатах
2 цикл Ренкина в pv и Ts координатах
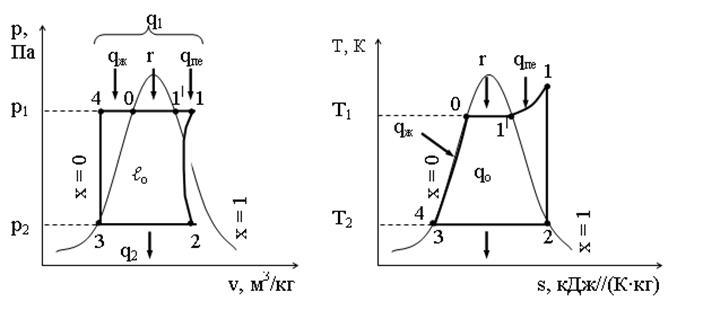
Рисунок 2 – Цикл Ренкина в pv — и Ts-координатах
· т. 4 – состояние воды при выходе из насоса 6 и входе в котел 1 при 0 °С и х = 0; степень сухости пара «х» (паросодержание) – отношение массы сухого насыщенного пара к массе смеси (воды и пара), кг;
· 4-0 – процесс изобарного подвода теплоты qж в котел 1 для нагрева воды от 0 °С до tк °С;
· т. 0 – состояние воды при tк °С;
· 0-1| – процесс изобарного и одновременно изотермического парообразования в котле 1 от х = 0 до х = 1 за счет скрытой удельной теплоты парообразования r – это количество теплоты, необходимое для перевода при р = const 1 кг жидкости (воды), нагретой до tнас в сухой насыщенный пар;
· т. 1| – состояние пара при выходе из котла 1 и входе в пароперегреватель 2;
· 1|-1 – процесс изобарного перегрева пара в пароперегревателе 2 с подводом теплоты qпе;
· т. 1 – состояние пара при выходе из пароперегревателя 2 и входе в паровую турбину 3;
· 1-2 – процесс адиабатного расширения пара в паровой турбине 3 с изменением давления от р1 до р2;
· т. 2 – состояние пара при выходе из паровой турбины 3 и входе в конденсатор 5;
· 2-3 – процесс изобарной конденсации пара в конденсаторе 5 с отводом теплоты q2 и изменением состояния рабочего пара от х = 1 до х = 0;
· т. 3 – состояние конденсата при выходе из конденсатора 5 и входе в насос 6;
· 3-4 – процесс изотермического нагнетания воды в котел 1 насосом 6 с повышением давления от р3 до р4.
3 расчет
3.1 термический КПД цикла Ренкина ηt
термический КПД цикла можно определить, как в любом цикле:
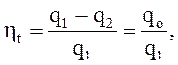 (1)
(1)
где q1, q2 – подведенная и отведенная удельная теплота в цикле, кДж/кг;
qo – удельная теплота цикла.
q1 = cp(t1 – t4) = i1 – i4; q2 = cp(t2 – t3) = i2 – i3.
Тогда термический КПД ηt цикла можно определить как:
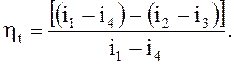 (2)
(2)
Если не учитывать ничтожного малого повышения температуры при адиабатном сжатии воды в насосе, то i3 = i4, а i3 – удельная энтальпия воды, кДж/кг, ![]() = срtводы, где ср – удельная теплота воды при постоянном давлении, кДж/(кг·К), ср = 4,19, тогда
= срtводы, где ср – удельная теплота воды при постоянном давлении, кДж/(кг·К), ср = 4,19, тогда 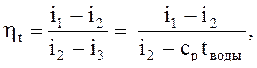 (3)
(3)
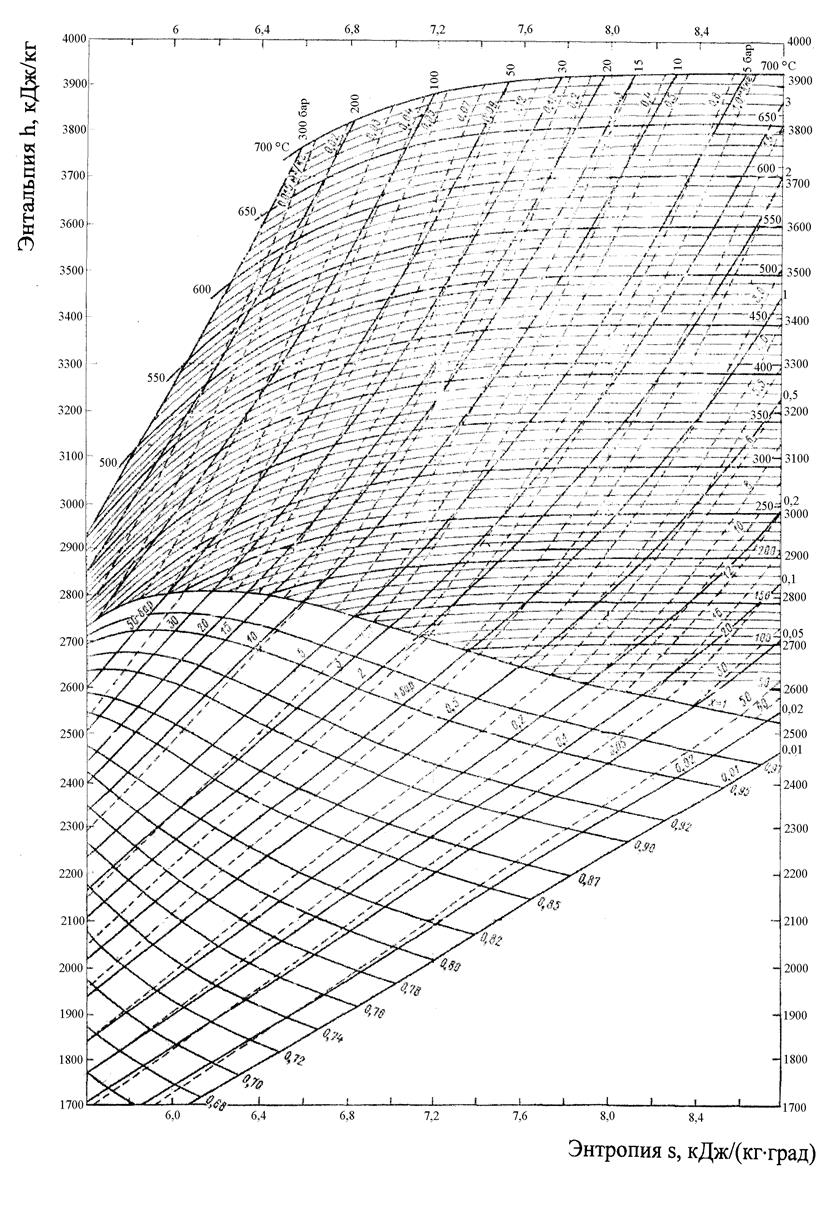
Значения энтальпий i1, i2 и температуру воды tводы (конденсата) находим по диаграмме is(sh), алгоритм нахождения приведен на рисунке 3.
i1 = 3 280 кдж/кг; i2 = 2 290 кДж/кг; t2 = 28 °С;
i2| = 4,19·28 = 117,32 кДж/кг.
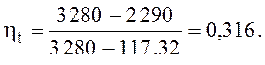
i1| = 3 550 кдж/кг; i2| = 2 200 кДж/кг; t2 = 28 °С; i3 = 4,19×28 = 117,32 кДж/кг.

3.2 удельный расход пара dо кг/(кВт-ч), идущего на выработку 1 кВт-ч энергии, 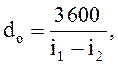 (4)
(4)
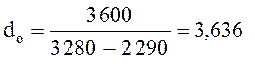 кг/ кВт·ч.
кг/ кВт·ч.
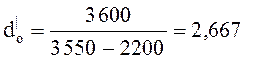 кг/кВт·ч;
кг/кВт·ч;
3.3 удельный расход пара d0 идущего на выработку единицы выполненной работы, кг /МДж,
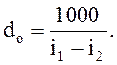 (5)
(5)
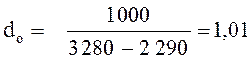 кг/МДж.
кг/МДж.
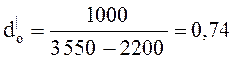 кг/МДж.
кг/МДж.
4 выкопировка из s—i (h) диаграммы расчетных процессов расширения пара в паровой турбине
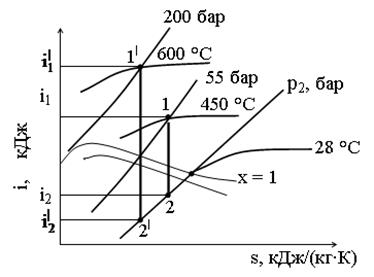
Рисунок 3 – Определение энтальпии пара в процессах цикла Ренкина по диаграмме в is
5 вывод о влиянии повышенных начальных параметров пара при поступлении в турбину
с повышением начальных параметров пара:
1) термический КПД цикла увеличивается;
2) количество пара dо, кг, уменьшается, идущего на выработку 1 кВт-ч энергии или на совершение 1 МДж работы;
3) идеальный цикл Ренкина в паросиловой установке по сравнению с идеальным циклом Карно:
· делает установку компактнее, так как насос по размерам значительно меньше компрессора;
· делает установку экономичнее, так как мощность насоса во много раз меньше мощности компрессора.
Задача № 5
цикл воздушно-компрессорной холодильной установки
Исходные параметры воздуха установки принять по таблице 1.
Таблица 1 – исходные данные для расчета цикла
|
№ п/п в жур-нале |
р1, мПа |
р2, мПа |
t1, ° C |
t3, ° C |
Q2, кВт |
№ п/п в жур-нале |
р1, мПа |
р2, мПа |
t1, ° C |
t3, ° C |
Q2, кВт |
|
1 |
0,1 |
0,4 |
– 10 |
17 |
100 |
16 |
0,1 |
0,5 |
– 10 |
18 |
160 |
|
2 |
0,1 |
0,4 |
– 12 |
16 |
110 |
17 |
0,1 |
0,5 |
– 9 |
20 |
150 |
|
3 |
0,1 |
0,4 |
– 14 |
20 |
120 |
18 |
0,1 |
0,5 |
– 8 |
21 |
140 |
|
4 |
0,1 |
0,4 |
– 8 |
22 |
130 |
19 |
0,1 |
0,5 |
– 7 |
22 |
130 |
|
5 |
0,1 |
0,4 |
– 6 |
25 |
140 |
20 |
0,1 |
0,5 |
– 6 |
23 |
120 |
|
6 |
0,1 |
0,4 |
– 4 |
19 |
150 |
21 |
0,1 |
0,5 |
– 5 |
24 |
110 |
|
7 |
0,1 |
0,4 |
– 2 |
18 |
160 |
22 |
0,1 |
0,5 |
– 4 |
25 |
100 |
|
8 |
0,1 |
0,4 |
– 5 |
23 |
170 |
23 |
0,1 |
0,5 |
– 2 |
15 |
90 |
|
9 |
0,1 |
0,4 |
– 7 |
15 |
180 |
24 |
0,1 |
0,7 |
– 3 |
19 |
100 |
|
10 |
0,1 |
0,4 |
– 9 |
26 |
190 |
25 |
0,1 |
0,7 |
– 4 |
20 |
100 |
|
11 |
0,1 |
0,6 |
– 10 |
27 |
200 |
26 |
0,1 |
0,7 |
– 5 |
21 |
110 |
|
12 |
0,1 |
0,6 |
– 12 |
25 |
180 |
27 |
0,1 |
0,7 |
– 6 |
22 |
120 |
|
13 |
0,1 |
0,6 |
– 14 |
23 |
160 |
28 |
0,1 |
0,7 |
– 7 |
23 |
130 |
|
14 |
0,1 |
0,6 |
– 15 |
20 |
150 |
29 |
0,1 |
0,7 |
– 8 |
24 |
140 |
|
15 |
0,1 |
0,6 |
– 13 |
18 |
140 |
30 |
0,1 |
0,7 |
– 10 |
20 |
150 |
1. Вычертить принципиальную схему воздушно-компрессорной установки, обозначить позициями ее основные элементы и записать их наименование.
2. рассчитать идеальной цикл воздушно-компрессорной холодильной установки.
2.1. определить неизвестные параметры в узловых точках цикла.
2.2. Определить изменение удельной энтропии ∆s, кдж/(кг·K).
2.3. определить удельную тепловую мощность теплообменника 3 q1, кДж/кг.
2.4. Определить удельную производительность холода холодильной камеры q2, кДж/кг,
2.5. определить расход воздуха М, кг/с.
2.6. определить удельную теоретическую потребляемую мощность (теплоту цикла) qо (кДж/кг) и полную мощность Qо (кВт).
2.7. определить холодильный коэффициент ε.
3. Вычертить цикл установки в pv и Ts-координатах по данным расчета, обозначить узловые точки цикла.
4. ответить на контрольные вопросы:
· что такое холодильный коэффициент?
· за счет чего работают компрессорные холодильные установки?
· чем определяется работа, затраченная на осуществление цикла в данной холодильной установке?
общие теоретические положения
процесс, в течение которого газ, претерпевает ряд изменений своего состояния и вновь возвращается в исходное состояние, называется круговым процессом или циклом.
Холодильные установки предназначены для искусственного охлаждения тел ниже температуры окружающей среды. Рабочее тело в холодильных установках совершает обратный круговой процесс, в котором затрачиваемая внешняя работа расходуется на отъем тепла от охлаждаемого тела. В воздушно-компрессорной холодильной установке рабочим телом является воздух.
Для получения низких температур (производства холода) в данном типе установки используют адиабатное расширение воздуха. Для этого его предварительно сжимают в компрессоре 1, а затем, так как при сжатии температура его повышается, охлаждают до температуры, например, окружающей среды в теплообменнике 2.
Если такой воздух заставить расширятся в расширительном сосуде 3 по адиабате, то он совершит работу за счет своей энергии, при этом его температура понизится и окажется ниже температуры окружающей среды. Охлажденный воздух поступает в холодильную камеру (охлаждаемое помещение) 4, отнимая теплоту от охлаждаемых тел, нагревается и вновь поступает в компрессор 1.
Схема воздушно-компрессорной холодильной установки представлена на рисунке 1.
Установка состоит из следующих элементов:
· компрессора 1, всасывающего воздух и сжимающий его;
· охладителя (теплообменника) 2, в котором охлаждается сжатый воздух водой;
· расширительного цилиндра 3, в котором воздух расширяется, совершая при этом работу и понижая свою температуру;
· холодильной камеры 4, в которой по трубопроводам циркулирует охлажденный воздух, отнимая теплоту от охлаждаемых тел, нагревается и вновь поступает в компрессор 1.

1 – компрессор; 2 – охладитель воздуха (теплообменник);
3 – расширительный цилиндр (детандер);
4 – холодильная камера
Рисунок 1 – Принципиальная схема воздушно-компрессорной
холодильной установки

Рисунок 2 – Теоретический цикл холодильной установки в координатах pv и Ts
На рисунке 2 (теоретический цикл воздушно компрессорной установки в pv и Тs координатах):
· точка 1 – состояние воздуха, поступающего в компрессор;
· линия 1-2 – адиабатный процесс сжатия в компрессоре;
· точка 2 – состояние воздуха, поступающего в охладитель (теплообменник);
· 2 -3 – изобарное охлаждение в теплообменнике;
· точка 3 – состояние воздуха, поступающего в расширительный цилиндр;
· 3 — 4 – адиабатный процесс расширения в расширительном цилиндре;
· точка 4 – состояние воздуха, поступающего в холодильную камеру;
· линия 4-1 –изобарное нагревание воздуха в холодильной камере;
· площадь 1-2-3-6-5- 4-1 – работа, затраченная компрессором на сжатие;
· площадь 3-6-5-4-3 – работа, полученная в расширительном цилиндре;
· площадь 1-2-3-4 – работа цикла.
На диаграмме в координатах Ts:
· площадь под кривой 4-1 – количество теплоты q2, переданной охлаждаемыми телами (пл. 1-4-6-5-1) воздуху в холодильной камере;
· площадь под кривой 3-2 – количество теплоты q1, отданной в охладителе (пл. 2-3-6-5-2) от воздуха воде;
· площадь 1-2- 3-4-1 – удельная теплота цикла qо1.
удельная производительность холода холодильной камеры 4 q2, кДж/кг.
q2 = cp m(T1 – T4), (1)
где T1 – температура воздуха, К, выходящего из холодильной камеры 4 и поступающего в компрессор 1;
T4 – температура воздуха, К, входящего в холодильную камеру 4;
cpm – удельная средняя теплоемкость воздуха при постоянном давлении, Дж/(кг·К).
удельная тепловая мощность теплообменника 2 q1, кДж/кг.
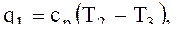 (2)
(2)
где T2 – температура воздуха, K, входящего в ![]() теплообменник 2;
теплообменник 2;
T3 – температура воздуха, K, входящего расширитель 3.
Удельная работа ℓк, Дж/кг, затраченная на привод компрессора 1:
ℓк = cp m(T1 – T2). (3.а)
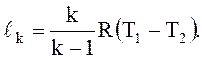 (3.б)
(3.б)
Удельная работа ℓр ц, Дж/кг, полученная в расширительном цилиндре 3:
ℓр. ц = cp m(T3 – T4). (4.а)
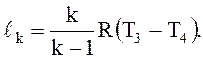 (4.б)
(4.б)
Удельная работа ℓо, Дж/кг, затраченная в цикле:
ℓо = ℓк – ℓр. ц. (5)
Расход холодильного агента (воздуха) М, кг/с,
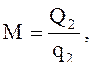 (6)
(6)
где Q2, q2 – соответственно холодопроизводительность установки, кДж, и удельная холодопроизводительность, кДж/кг.
Холодильный коэффициент:
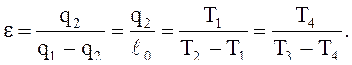 (7.а)
(7.а)
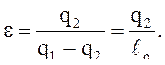 (7.б)
(7.б)
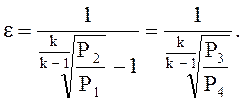 (7.в)
(7.в)
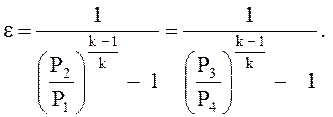 (7.с)
(7.с)
Пример расчета
Дано: р1 = 0,1 мПа; р2 = 0,7 мПа;
t1 = – 10 °C; T1 = 263 K; t3 = 20 ° C;
T3 = 293 K; Q2 (Qх) = 150 кВт.
решение

1 – компрессор; 2 – теплообменник (охладитель);
3 – расширительный цилиндр; 4 – холодильная камера
Рисунок 1 – Принципиальная схема воздушно-компрессорной холодильной установки
2 Расчет идеального цикла
2.1 определение неизвестных параметров в узловых точках цикла
точка 1: р1 = 0,1 МПа; Т1 = 263 K.
удельный объем v1 определим из уравнения состояния:
p1v1 = RT1, (1)
где р1 – давление в начале сжатия, Па; v1 – дельный объем в начале сжатия, м3/кг; R – газовая постоянная воздуха, Дж/(кг·К), R = 287; Т1 – температура в начале сжатия, К.
уравнение (1) выразим относительно удельного объема v1.
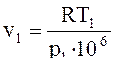 .
.
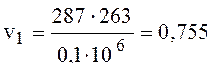 м3/кг;
м3/кг;
давление: р1 = 0,1 мПа. температура: Т1 = 263 K.
точка 2: р2 = 0,7 мПа; процесс 1-2 – адиабатное сжатие.
Уравнение адиабатного процесса: p1v1к = p2 v2к. (2)
где к – коэффициент адиабаты, к = 1,4.
удельный объем v2, м3/кг, определим из уравнения (2):
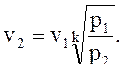
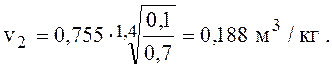
температуру Т2, К, определим из формулы (1) относительно точки 2. 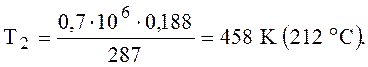
точка 3: р3 = р2 = 0,7 мПа, так как процесс 2-3 – изобарное охлаждение в теплообменнике; температура: T3 = 293 K.
удельный объем v3, м3/кг, определим по формуле (1) относительно точки 3.
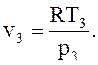
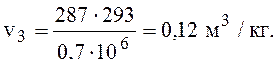
точка 4: р4 = р1 = 0,1 мПа, так как процесс 4-1 – изобарный нагрев в холодильной камере.
удельный объем v3, м3/кг, определим по формуле (2) относительно точки 4, так как процесс 3-4 – адиабатное расширение в детандере:
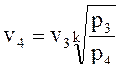 .
.
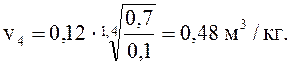
температуру Т4 определим по формуле (1) относительно точки 4:
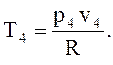
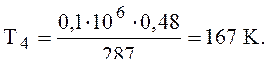
2.2 Определение изменение удельной энтропии ∆s
Процесс 1-2 – адиабатный, поэтому изменение энтропии ∆s1-2 = 0
Процесс 2-3 – изобарный, поэтому изменение удельной энтропии ∆s, кДж/(кг·К):
∆s2-3 = 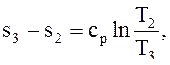 (3)
(3)
где ср – удельная теплоемкость воздуха при постоянном давлении, кДж/(кг·К), ср = 1,009.
∆s3-2 = 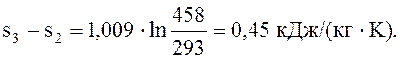
Процесс 3-4 – адиабатный, поэтому изменение удельной энтропии
∆s3-4 = 0.
Процесс 4-1 – изобарный, поэтому изменение удельной энтропии ∆s, кДж/(кг·К), определяем по формуле (3) относительно данного процесса.
∆s4-1 = 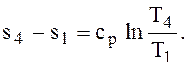 (4)
(4)
∆s1-4 = 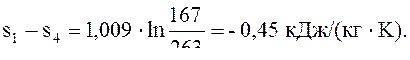
2.3 определение удельной тепловой мощности q1, кДж/кг, теплообменника 2.
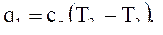 (5)
(5)
кДж/кг.
2.4 Определение удельной производительности холода холодильной камеры q2, кДж/кг, по формуле (5):
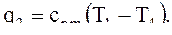 (6)
(6)
![]() Дж/кг.
Дж/кг.
2.5 определение расхода воздуха М
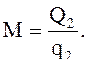 (7)
(7)
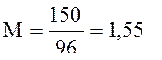 кг/с.
кг/с.
2.6 Определение удельной теплоты qо и теплоты Qо цикла
qo = q2 – q1. (8)
qo = 166,5 – 96 = 70,5 кДж/кг.
 . (9)
. (9)
Qо = 1,55 ×70,5= 109 кВт.
2.7 Определение холодильного коэффициента
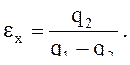 (10.а)
(10.а)
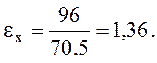
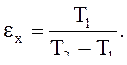 (10.б)
(10.б)
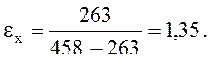
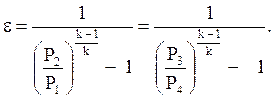 (10.в)
(10.в)
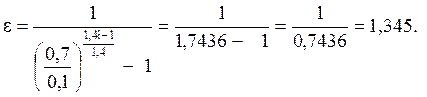
3 цикл установки в координатах pv и Ts

1-2 – адиабатное сжатие в компрессоре; 2-3 – изобарное охлаждение в теплообменнике; 3-4 – адиабатное расширение в детандере;
4-1 – изобарный нагрев в холодильной камере
Рисунок 2 – Цикл холодильной установки в pv и Ts координатах
Задача № 6
рекуперативный теплообменный аппарат типа «Труба в трубе»
Таблица 1 – Исходные данные
|
Пара-метры |
Номер варианта |
||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
|
400 |
370 |
450 |
415 |
385 |
460 |
510 |
500 |
480 |
390 |
400 |
370 |
450 |
415 |
385 |
|
|
165 |
200 |
215 |
250 |
260 |
270 |
280 |
230 |
250 |
225 |
165 |
200 |
215 |
250 |
260 |
|
|
5 |
5 |
5 |
5 |
5 |
10 |
10 |
10 |
10 |
15 |
15 |
15 |
15 |
15 |
15 |
|
|
80 |
80 |
80 |
80 |
80 |
140 |
75 |
75 |
75 |
70 |
70 |
65 |
65 |
65 |
65 |
|
М1, кг/с |
1,5 |
– |
1,8 |
– |
1,5 |
– |
1,8 |
– |
2,0 |
– |
2,0 |
– |
2,4 |
– |
2,4 |
|
М2, кг/с |
– |
4,5 |
– |
4,0 |
– |
3,5 |
– |
3,0 |
– |
2,5 |
– |
2,0 |
– |
1,5 |
– |
|
α1·10–1 |
42 |
42 |
40 |
40 |
38 |
38 |
35 |
35 |
32 |
32 |
30 |
30 |
28 |
28 |
26 |
|
α2·10–2 |
26 |
42 |
28 |
35 |
30 |
30 |
32 |
28 |
35 |
25 |
38 |
20 |
40 |
23 |
27 |
|
Распо-ложе-ние труб |
Г |
Г |
В |
В |
Г |
Г |
В |
В |
Г |
Г |
В |
В |
Г |
Г |
В |
|
матер. |
С |
Л |
С |
Л |
С |
Л |
С |
Л |
С |
Л |
С |
Л |
С |
Л |
С |
Продолжение таблицы 1
|
Пара-метры |
Номер варианта |
||||||||||||||
|
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
|
|
400 |
370 |
450 |
415 |
385 |
460 |
510 |
500 |
480 |
390 |
400 |
370 |
450 |
415 |
385 |
|
|
165 |
200 |
215 |
250 |
260 |
270 |
280 |
230 |
250 |
225 |
165 |
200 |
215 |
250 |
260 |
|
|
20 |
20 |
20 |
20 |
20 |
25 |
25 |
25 |
25 |
25 |
30 |
30 |
30 |
30 |
30 |
|
|
60 |
60 |
60 |
60 |
65 |
65 |
65 |
65 |
70 |
70 |
70 |
70 |
75 |
75 |
75 |
|
М1, кг/с |
0,5 |
– |
0,8 |
– |
1,5 |
– |
1,8 |
– |
2,0 |
– |
2,2 |
– |
2,4 |
– |
2,6 |
|
М2, кг/с |
– |
4,5 |
– |
4,0 |
– |
3,5 |
– |
3,0 |
– |
2,5 |
– |
2,0 |
– |
1,5 |
– |
|
α1·10–1 |
42 |
42 |
40 |
40 |
38 |
38 |
35 |
35 |
32 |
32 |
30 |
30 |
28 |
28 |
26 |
|
α2·10–2 |
26 |
42 |
28 |
35 |
30 |
30 |
32 |
28 |
35 |
25 |
38 |
20 |
40 |
23 |
27 |
|
Распо-ложе-ние труб |
Г |
Г |
В |
В |
Г |
Г |
В |
В |
Г |
Г |
В |
В |
Г |
Г |
В |
|
матер. |
С |
Л |
С |
Л |
С |
Л |
С |
Л |
С |
Л |
С |
Л |
С |
Л |
С |
Греющий теплоноситель – дымовые газы, которые движутся в межтрубном пространстве.
нагреваемый теплоноситель – вода, которая движется по внутренней трубе.
Теплообменник выполнен из металлических труб.
Параметры:
· ![]() – начальная температура греющего теплоносителя, ° С;
– начальная температура греющего теплоносителя, ° С;
· ![]() конечная температура греющего теплоносителя, ° С;
конечная температура греющего теплоносителя, ° С;
· ![]() – начальная температура нагреваемого теплоносителя, ° С;
– начальная температура нагреваемого теплоносителя, ° С;
· ![]() – конечная температура нагреваемого теплоносителя, ° С;
– конечная температура нагреваемого теплоносителя, ° С;
· М1 – расход греющего теплоносителя, кг/с;
· М2 – расход нагреваемого теплоносителя, кг/с;
· α1 – коэффициент теплоотдачи от греющего теплоносителя к поверхности внутренней трубы, Вт/(м2×К);
· α2 – коэффициент теплоотдачи от поверхности внутренней трубы к нагреваемому теплоносителю, Вт/(м2×К);
· d1, d2 – внутренний и наружный диаметр внутренней трубы, м, d1 = 33·10 –3, d2 = 38·10 –3, δ – толщина стенки труб, м, δ = 10 –3(38 – 33)/2 = 2,5·10 – 3 = 0,0025;
· материал труб: сталь – С; латунь – Л;
· расположение труб: горизонтальное – Г; вертикальное – В;
· λ – коэффициент теплопроводности материала стенки труб, Вт/(м×К): сталь – 50; латунь – 100.
Задание
1. определить
(для прямоточной и противоточной схемы движения теплоносителей):
1.1) тепловую мощность Q, Вт, передаваемую от греющего теплоносителя к нагреваемому теплоносителю;
1.2) неизвестный расход М, кг/с, одного из теплоносителей;
1.3) средний температурный напор ∆ tср;
1.4) коэффициент теплоотдачи k, Вт/ (м2×K);
1.5) площадь поверхности нагрева F, м2.
2. Вычертить по результатам расчета графики изменения температуры теплоносителей при прямоточной и противоточной схеме движения теплоносителей и принципиальную схему теплообменника.
3. выводы.
4. ответить на контрольные вопросы:
· какое устройство называется теплообменным аппаратом?
· какие типы теплообменных аппаратов вы знаете?
· схемы движения теплоносителей в теплообменных аппаратах?
· какие уравнения положены в основу теплового расчета теплообменнников?
· какие процессы передачи теплоты происходят в рекуперативном теплообменнике «труба в трубе»?
· в каком случае можно рассчитывать коэффициент теплопередач по формулам полоской пластины?
общие теоретические положения
Устройства, предназначенные для передачи теплоты от одной среды к другой, называют теплообменными аппаратами или теплообменниками.
Среды, участвующие в процессе теплообмена, называют теплоносителями. Теплоносителями могут быть газы, жидкости, пары.
1. По принципу действия и конструктивному исполнению все устройства подразделяются на теплообменники:
· поверхностные;
· контактные (смесительные);
· с внутренним источником теплоты.
Поверхностные теплообменники – устройства, в которых процесс передачи теплоты связан с поверхностью твердого тела, то есть теплообмен от одной среды к другой происходит через разделительную стенку. Они, в свою очередь, разделяются на теплообменники: рекуперативные; регенеративные.
Рекуперативные поверхностные теплообменники – такие устройства, где два теплоносителя с различными температурами текут в пространствах, разделенных твердой стенкой (калориферы, отопительные приборы, конденсаторы, парогенераторы).


