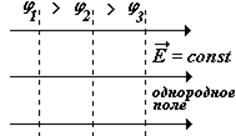Циркуляция вектора напряженности
|
|
Циркуляция вектора напряженности электростатического поля равна нулю. [6] Это является условием потенциальности поля. |
Работа консервативных (потенциальных) сил равна убыли потенциальной энергии тела. Следовательно, можно ввести еще одну характеристику электростатического поля – потенциал j.
|
(В = Дж/Кл) |
потенциал (скаляр) – энергетическая характеристика электростатического [7] поля — по смыслу это: 1) потенциальная энергия, которой обладает единичный положительный заряд, помещенный в данную точку поля или 2) работа, которую надо совершить, чтобы перенести единичный положительный заряд из данной точки 1 в бесконечность (¥). |
|
|
разность потенциалов – это работа, которую надо совершить, чтобы переместить единичный положительный заряд из точки 1 в точку 2 |
Найдем связь между напряженностью и потенциалом.
|
|
работа в потенциальном (консервативном) поле равна убыли потенциальной энергии |
|
|
|
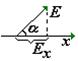
выразим элементарную работу через напряженность и разность потенциалов; сократим на q, обозначим проекцию вектора Е на направление х как Ех, получим: |
|
|
|
связь между Е и j в дифференциальной форме для одномерного случая, когда потенциал зависит только от координаты х — j (х) |
|
|
|
В трехмерном случае, когда потенциал является функцией j (х,y,z), запишем формулы для каждой проекции и, объединяя их в одно выражение, найдем (учитывая, что Е — вектор): |
|
Ñ («набла») — другое обозначение градиента |
Напряженность электростатического поля равна градиенту потенциала, взятому с обратным знаком. |
Градиент – это вектор, показывающий направление наибольшего роста скалярной функции (в нашем случае — потенциала).[8] В одномерном случае градиент напряженности dj / dx приобретает простой физический смысл: он показывает, на сколько изменяется потенциал на единице длины.
«-» в правой части формул означает, что вектор напряженности Е всегда направлен в сторону убывания потенциала.
Из приведенных выражений, зная j (х,y,z), можно, дифференцируя, найти напряженность поля. Производя обратную операцию – интегрирование, можно при известной напряженности найти потенциал. Рассмотрим случай зависимости
Е и j только от одной переменной х. Из формулы (··) находим:
|
|
Связь разности потенциалов с напряженностью в интегральной форме для одномерного случая, когда Е(х) |
Графическое изображение электростатического поля.
Электростатическое поле удобно изображать графически с помощью силовых линий и эквипотенциальных поверхностей.
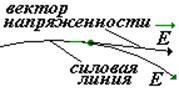 Силовая линия – это линия, в каждой точке которой касательная совпадает с направлением вектора напряженности (см. рис.). Силовым линиям придают направление стрелкой. Свойства силовых линий:
Силовая линия – это линия, в каждой точке которой касательная совпадает с направлением вектора напряженности (см. рис.). Силовым линиям придают направление стрелкой. Свойства силовых линий:
1) Силовые линии непрерывны. Они имеют начало и конец – начинаются на положительных и заканчиваются на отрицательных зарядах.
2) Силовые линии не могут пересекаться друг с другом, т. к. напряженность – это сила, а две силы в данной точке от одного заряда не могут быть.
3) Силовые линии проводят так, чтобы их количество через единичную перпендикулярную площадку было пропорционально величине напряженности.
4) Силовые линии «выходят» и «входят» всегда перпендикулярно поверхности тела.
5) Силовую линию не следует путать с траекторией движущегося заряда. Касательная к траектории совпадает с направлением скорости, а касательная к силовой линии – с силой и, следовательно, с ускорением.
Эквипотенциальной поверхностью называют поверхность, в каждой точке которой потенциал имеет одинаковое значение j = const.
Силовые линии всегда перпендикулярны эквипотенциальным поверхностям. Докажем это. Пусть вдоль эквипотенциальной поверхности перемещается точечный заряд q. Элементарная работа, совершаемая при этом равна dA=qE×cosa×dl = q×dj = 0, т. к. dj = 0. Поскольку q ,E и ×dl ¹ 0, следовательно
cosa = 0 и a = 90о.
|
|
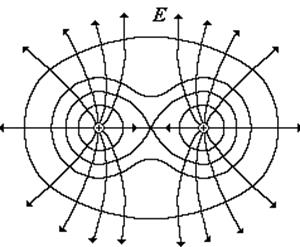
На рисунке изображено электростатическое поле двух одинаковых точечных зарядов. Линии со стрелками – это силовые линии, замкнутые кривые – эквипотенциальные поверхности. В центре осевой линии, соединяющей заряды напряженность равна 0. На очень большом расстоянии от зарядов эквипотенциальные поверхности становятся сферическими. . |
|
|
На этом рисунке показано однородное поле – это поле, в каждой точке которого вектор напряженности остается постоянным по величине и направлению Эквипотенциальные поверхности – это плоскости, перпендикулярные силовым линиям. Вектор напряженности всегда направлен в сторону убывания потенциала. |
Принцип суперпозиции.
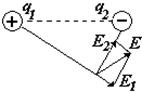
На основе опытных данных был получен принципа суперпозиции (наложения) полей: «Если электрическое поле создается несколькими зарядами, то напряженность и потенциал результирующего поля складываются независимо, т. е. не влияя друг на друга». При дискретном распределении зарядов напряженность результирующего поля равна векторной сумме, а потенциал алгебраической (с учетом знака) сумме полей, создаваемых каждым зарядом в отдельности. При непрерывном распределении заряда в теле векторные суммы заменяется на интегралы, где dE и dj– напряженность и потенциал поля элементарного (точечного) заряда, выделенного в теле. Математически принцип суперпозиции можно записать так.
|
|
|
при дискретном распределении зарядов |
принцип суперпозиции |
Рефераты по физике сдают здесь
Другие статьиПохожая информацияУзнать стоимость за 15 минут
Распродажа дипломных
Подпишись на наш паблик в ВК
Нужна работа?
|
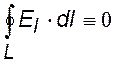
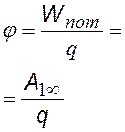
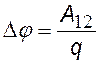
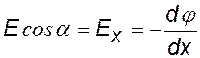 (··)
(··)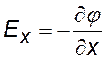
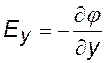
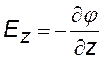
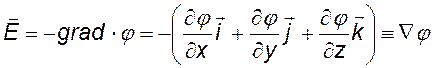
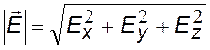 (модуль вектора Е)
(модуль вектора Е)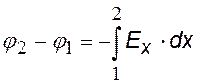 (···)
(···)