ПРИМЕНЕНИЕ ОБЩЕГО УРАВНЕНИЯ ДИНАМИКИ

ПРИМЕНЕНИЕ ОБЩЕГО УРАВНЕНИЯ ДИНАМИКИ

И УРАВНЕНИЙ ЛАГРАНЖА ВТОРОГО РОДА ПРИ ИССЛЕДОВАНИИ ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ

Учебно-методическое пособие

к расчетно-графической работе по теоретической механике

ПРИМЕНЕНИЕ ОБЩЕГО (ОБОБЩЕННОГО) УРАВНЕНИЯ

ДИНАМИКИ И УРАВНЕНИЙ ЛАГРАНЖА ВТОРОГО РОДА

ПРИ ИССЛЕДОВАНИИ ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ

СИСТЕМЫ

Краткие сведения из теории

Общее (обобщенное) уравнение динамики

Общее уравнение динамики является аналогом принципа возможных перемещений для случая движения системы материальных точек.

При движении механической системы, на которую наложены двусторонние, стационарные, голономные и идеальные связи, сумма возможных (элементарных) работ всех активных сил, приложенных к механической системе, и сумма возможных (элементарных) работ сил инерции всех материальных точек или тел, входящих в эту механическую систему, на любом возможном ее перемещении равна нулю:

.

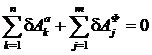Возможными (или виртуальными) перемещениями несвободной механической системы называются воображаемые бесконечно малые перемещения, допускаемые в данный момент наложенными на систему связями.

Число степеней свободы механической системы – это число ее независимых возможных перемещений, которые можно сообщить точкам системы в фиксированный момент времени.

Приведение сил инерции механической системы

Главный вектор сил инерции любой механической системы направлен в сторону, обратную направлению ускорения её центра масс. Величина главного вектора сил инерции равна произведению массы механической системы на ускорение её центра масс.

.

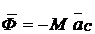Главный момент сил инерции симметричного твердого тела относительно его центральной оси равен произведению осевого момента инерции этого тела относительно центральной оси на угловое ускорение тела и направлен в сторону, обратную направлению ускорения этого тела.

.

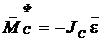Возможная (элементарная) работа силы – бесконечно малая скалярная величина, равная скалярному произведению вектора силы на вектор возможного перемещения точки её приложения:

.

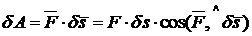Связи и их классификация

Связи – любые ограничения в виде тел или каких-либо кинематических условий, накладываемые на движения точек механической системы. Эти ограничения могут быть записаны в виде уравнений или неравенств.

Нестационарные связи – связи, изменяющиеся с течением времени, т. е. в уравнения которых явно входит время .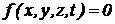

Стационарные связи – связи, в уравнения которых не входит явно время.

Геометрические связи – связи, уравнения которых содержат только координаты материальных точек, т. е. ограничения накладываются только на координаты точек. Это связи в виде тел, поверхностей, линий и т. п. Например, связь в виде некоторой поверхности описывается уравнением .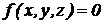

Кинематические связи – связи, уравнения которых содержат не только координаты материальных точек, но и проекции скоростей этих точек.

Дифференциальные связи – связи, накладывающие ограничения не только на координаты точек, но и на их скорости, описываются уравнением .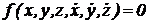

Связи называются голономными, если их уравнения могут быть записаны в виде, не содержащем производных от координат по времени или дифференциалов координат.

Неголономными связями называются дифференциальные связи, уравнения которых не могут быть проинтегрированы.

Двусторонние (удерживающие) связи – связи, ограничивающие движение точки в двух противоположных направлениях, уравнение связи дается в форме равенства.

Односторонние (неудерживающие) связи – связи, ограничивающие движение только в одном направлении, уравнение связи дается в форме неравенства.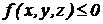

Уравнения Лагранжа второго рода представляют собой систему уравнений динамики в обобщенных координатах. Их использование является универсальным методом получения системы дифференциальных уравнений, описывающих движение любой механической системы.

Обобщенными координатами системы называется совокупность независимых параметров, которые однозначно определяют положение механической системы.

Обобщенные координаты обозначаются q1, q1,…, qN или qj(j=1,2,…,N). Производные по времени от обобщенных координат называются обобщенными скоростями 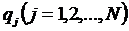. Число N независимых обобщенных координат голономной системы равно числу ее степеней свободы.

Уравнения Лагранжа второго рода имеют вид

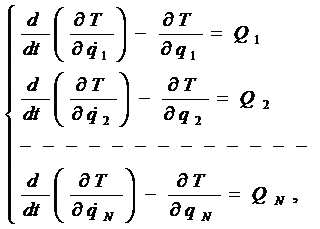
где Т – кинетическая энергия системы;

Qj – обобщенная сила, соответствующая j-й обобщенной координате.

Кинетическая энергия системы равна сумме кинетических энергий всех объектов, образующих систему (T = T1+T2+……+Tn).

Кинетическая энергия твердого тела определяется по формулам:

– при поступательном движении:

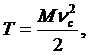Vс – скорость центра масс тела;

– при вращательном движении:

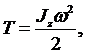Jz – момент инерции тела относительно оси вращения;

w – угловая скорость вращения;

– при плоскопараллельном движении:

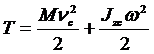, Jzc – момент инерции тела относительно оси, проходящей через центр масс перпендикулярно плоскости движения.

Величина 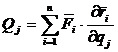называется j-й обобщенной силой.

Если вычислить сумму элементарных работ активных сил, действующих на точки системы на возможном перемещении системы, то соответствующая формула может быть представлена в виде:

.

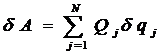Для определения обобщенной силы, соответствующей j-й обобщенной координате, необходимо:

1 Этой координате сообщить приращение 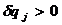, оставляя все остальные обобщенные координаты без изменений.

2 Вычислить сумму элементарных работ всех сил, действующих на систему, на этом перемещении.

3 Полученную работу разделить на приращение обобщенной координаты:

.

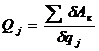При вычислении работы сил используются следующие формулы:

работа сил тяжести:

,

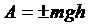h – изменение высоты между начальным и конечным положениями;

работа силы трения:

;

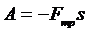работа постоянной силы на прямолинейном перемещении:

,

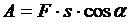a – угол между направлением силы и направлением перемещения;

работа сил, приложенных к вращающемуся телу:

,

Mz(F) – момент силы относительно оси вращения;

j – угол поворота тела.

Методика составления уравнений Лагранжа второго рода

Составление уравнений Лагранжа второго рода производится в следующем порядке:

1)  определяется число степеней свободы заданной механической системы;

2)  выбираются независимые обобщенные координаты, число которых равно числу степеней свободы;

3)  вычисляется кинетическая энергия Т рассматриваемой системы, которая выражается через обобщенные скорости;

4)  находятся частные производные кинетической энергии по обобщенным скоростям, т. е.

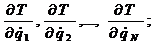
5) вычисляются их производные по времени

;

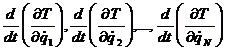6)  определяются частные производные кинетической энергии по обобщенным координатам

;

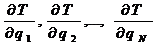7)  находятся обобщенные силы Q1, Q2,…QN , соответствующие выбранным обобщенным координатам;

8)  полученные в п. п. 4-6 результаты подставляются в уравнения Лагранжа.

Пример выполнения задания

УСЛОВИЕ ЗАДАЧИ:

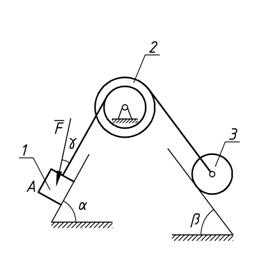
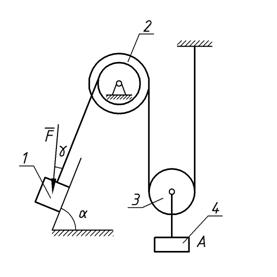
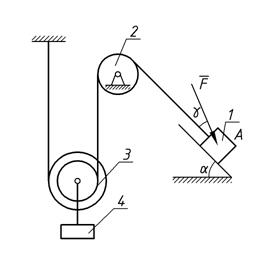
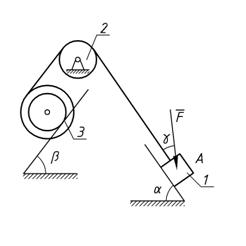
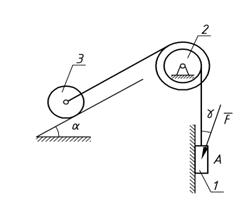
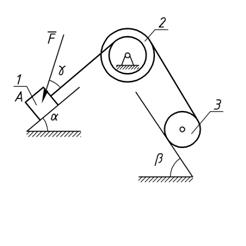
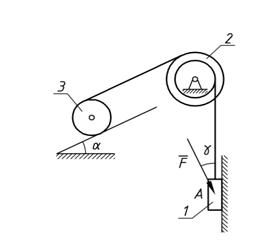
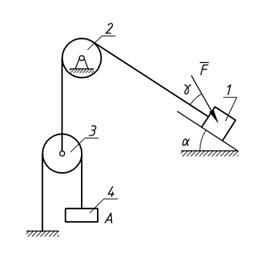
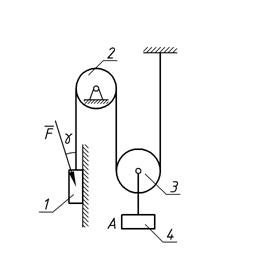
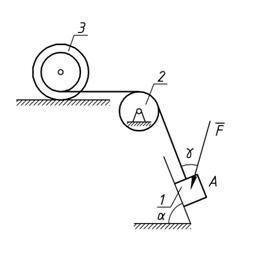
Механическая система состоит из грузов 1 и 4 и ступенчатых шкивов 2 и 3 с радиусами ступеней R2 = 0,3 м; r2 = 0,15 м и R3=0,2 м; r3 = 0,1м (или однородных дисков с радиусами R2 и R3). Если груз 4 на рисунке отсутствует, его массу не использовать). Радиусы инерции ступенчатых шкивов относительно их осей, проходящих через их центры масс, соответственно равны: r2 = 0,3 м и r3 = 0,1 м. Тела системы соединены друг с другом нитями, намотанными на шкивы; участки нитей параллельны соответствующим плоскостям. Механическая система движется в вертикальной плоскости под действием сил тяжести, силы F, направленной под углом к линии движения груза 1 и пары сил с моментом M, приложенной к шкиву 2 (момент действует против часовой стрелки). Исходные данные представлены в таблице 1 (стр. 15), а схемы механизмов – в таблице 2 (стр. 16– 20) . Определить ускорение тела, имеющего больший вес.

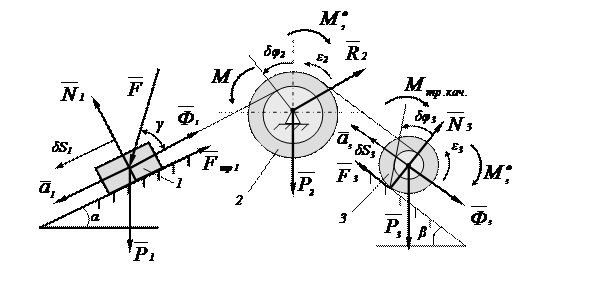Рис. 1

Рассмотрим задачу со следующими исходными данными:

m1(кг)	m2(кг)	m3(кг)	m4(кг)	M(Нм)	F(Н)	f1	f3	k3
40	30	20	–	80	25	0,2	0,1	0,01	300	600	450

Где mk ,Rk ,rk , – массы, радиусы блоков и радиусы инерции соответствующих тел,

fk и kk – коэффициенты трения и трения качения тел.

Указания к решению задачи

При определении кинематических характеристик механической системы можно воспользоваться общим уравнением динамики или уравнением Лагранжа второго рода.

I Рассмотрим 1-й способ:

Механизм в рассматриваемой задаче имеет одну степень свободы, т. е. одно независимое возможное перемещение.

Для решения задачи с помощью общего уравнения динамики нужно сообщить механизму возможное перемещение, вычислить сумму элементарных работ всех действующих активных сил и пар сил на этом перемещении, сложить с суммой элементарных работ всех сил инерции и моментов сил инерции на этом же перемещении и приравнять эту сумму к нулю. Все вошедшие в полученное уравнение возможные перемещения следует выразить через какое-нибудь одно (через возможное перемещение тела, ускорение которого нужно найти).

Решение:

На данную механическую систему с одной степенью свободы действует следующая система сил:

1) Активные силы:

=m1 – вес первого тела, движущегося поступательно;

=m2 – вес второго тела, совершающего вращательное движение;

=m3 – вес третьего тела, движущегося плоско-параллельно;

F – заданная внешняя сила, действующая на первое тело под углом к поверхности, по которой движется это тело;

М = 80 Нм — заданный момент пары сил, действующий на тело 2.

2) Силы реакций связей:

N1 =P1+ F1 нормальная составляющая реакции наклонной поверхности (ее определяем, проецируя основное уравнение динамики для первого тела на направление нормали: m =N1 –P1—F1 , учитываем, что =0).

Fтр1 =f1N1=f1(P1+ F1 ) – касательная составляющая реакции наклонной поверхности, направленная в сторону, противоположную движению;

– реакция цилиндрического шарнира, с помощью которого крепится блок 2.

N3=P3 – нормальная составляющая реакции наклонной поверхности на каток;

F3 =f3N3=f3P3 – касательная составляющая реакции наклонной поверхности на каток, направленная в сторону, противоположную движению;

Mтр. кач. = N3 = P3 – момент трения качения, действующего со стороны наклонной поверхности на каток и направленного в сторону, противоположную качению катка.

3) Добавим к рассматриваемой системе Даламберовы силы инерции:

а) Так как 1-ое тело движется поступательно, сила приложена в его центре масс:

= —m1 ;

б) силы инерции вращающегося тела 2 приводятся к моменту относительно неподвижной оси:

= J2 , где J2 = m2 – момент инерции блока 2, а

= — угловое ускорение блока 2;

в) так как третье тело движется плоскопараллельно, его силы инерции приводятся к силе= — m3 в центре масс катка 3 и моменту относительно центра масс = J3 , причем

а3= 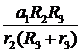, =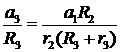; J3 =m3 .

Выразим через возможное перемещение груза 1 перемещения остальных тел:

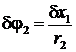, (аналогично, )

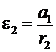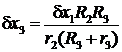, (аналогично, а3= ),

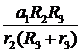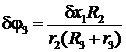, (аналогично, =).

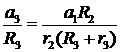Составим общее уравнение динамики для механической системы с одной степенью свободы:

(1)

Работа сил и равна нулю, т. к. их направления перпендикулярны перемещению.

Работа сил , равна нулю, т. к. все эти силы приложены к неподвижной точке.

Работа силы равна нулю, потому что она приложена в мгновенном центре скоростей катка (скорость точки приложения силы в данный момент равна нулю).

Учитывая связи между возможными перемещениями, выражения для сил и моментов инерции и подставляя их в (1), получаем:

или

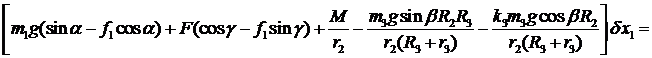
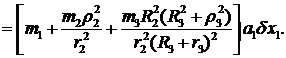
Так как 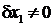, подставляя исходные данные, придем к уравнению относительно а1 :

442,62 = 204,44 а1 ,

решая которое, окончательно получим: a1 =2,165 м/с2

II Рассмотрим 2-й способ.

Решим эту же задачу, используя уравнение Лагранжа второго рода. Во всех вариантах система имеет одну степень свободы, и еe положение определяется одной обобщенной координатой q. Уравнение Лагранжа – это дифференциальное уравнение 2-го порядка относительно обобщенной координаты.

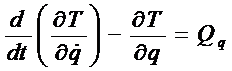. (1)

Если требуется определить ускорение a1, то за обобщенную координату целесообразно принять перемещение х этого тела, тогда 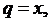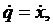– обобщенная скорость и уравнение (1) примет вид:

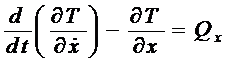. (2)

При определении углового ускорения e2 за обобщенную координату нужно принять угол поворота шкива, т. е. 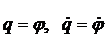и уравнение (1) будет иметь вид:

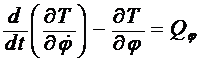. (3)

Для составления уравнения (2) или (3) необходимо:

1)  вычислить кинетическую энергию Т системы, выразив её через обобщенную скорость ( или ) и обобщенную координату q (x или j);

2)  вычислить обобщенную силу Qx или Qj, для определения которой сообщим системе возможное (малое) перемещение ( или );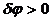

3)  вычислить сумму элементарных работ всех сил на этом перемещении, выразив эти перемещения через dx или dj .

Получим: 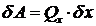или 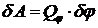. Коэффициенты при dx или dj в выражении dА и будут обобщенными силами.

Решение

1 Запишем уравнение Лагранжа второго рода для механической системы с одной степенью свободы:

,

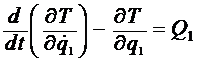где и q1 – обобщенные координаты и скорость соответственно. В качестве обобщенной координаты целесообразно выбрать перемещение первого тела:

q1 = x1 =x.

Тогда уравнение Лагранжа второго рода для рассматриваемой системы примет вид:

.

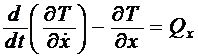2 Учитывая вид движения каждого тела системы, вычислим ее кинетискую энергию: T = T1 + T2 + T3 .

Тело 1 движется поступательно, значит: T1= .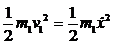

Шкив 2 вращается, следовательно: T2 =.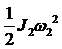

Каток 3 движется плоскопараллельно: T3 = .

Известно, что 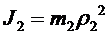, , 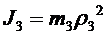а ,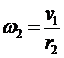

и .

Используя эти соотношения, получим, T2= ;

T3 = .

Тогда T = 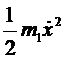++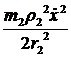 = 0,5,

где с = 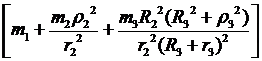= 204,44.

3 Определим обобщенную силу Qx . При движении системы совершать работу будут следующие силы: заданная сила , силы тяжести , сила трения, пара сил с заданным моментом М и момент трения качения Mтр. кач .

Сообщим системе возможное перемещение груза 1 в направлении его движения и покажем перемещения остальных тел:

тела 2 – угол поворота ;

катка 3 – центра масс и угол поворота относительно центра масс . Вычислим сумму элементарных работ всех сил на этих перемещениях: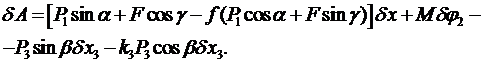

Учтем соотношения между возможными перемещениями:

, , .

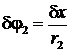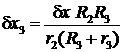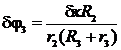В результате получим:

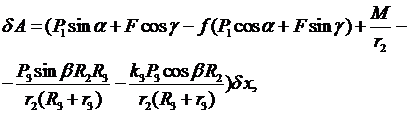
откуда .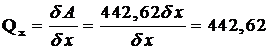

Подставляя все полученные выражения в уравнение (1), запишем:

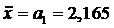м/с2.

Таблица 1
Исходные данные

№	m1(кг)	m2(кг)	m3(кг)	m4(кг)	M(Нм)	F(Н)	f1	f3	k3
1	42	36	24	15	80	25	0.2	0.1	0.01	300	600	450
2	20	18	12	10	40	20	0.15	0.3	0.02	450	300	300
3	35	25	15	8	60	40	0.1	0.2	0.01	600	300	450
4	45	28	30	12	50	30	0.3	0.2	0.03	450	600	450
5	28	32	25	16	40	35	0.11	0.12	0.02	600	450	450

Таблица 2
Расчетные схемы механизмов

Рис. Д5–1	Рис. Д5–2
Рис. Д5–3	Рис. Д5–4
Рис. Д5–5	Рис. Д –6

Продолжение табл. 2

Рис. Д5–7	Рис. Д5–8
Рис. Д5–9	Рис. Д5–10
Рис. Д5–11	Рис. Д5–12

Продолжение табл. 2

Рис. Д5–13	Рис. Д5–14
Рис. Д5–15	Рис. Д5–16
Рис. Д5–17	Рис. Д5–18

Продолжение табл.2

Рис. Д5–19	Рис. Д5–20
Рис. Д5–21	Рис. Д5–22
Рис. Д5–23	Рис. Д5–24

Окончание табл.2

Рис. Д5–25	Рис. Д5–26
Рис. Д5–27	Рис. Д5–28
Рис. Д5–29	Рис. Д5–30

Библиографический список

1 Никитин, Н. Н. Курс теоретической механики: учебник для машиностроит. и приборостроит. спец. вузов / Н. Н. Никитин. – М. : Высш. шк., 2010. – 607 с.

2 Бать, М. И. Теоретическая механика в примерах и задачах. Т.2. Динамика: учеб. пособие / М. И. Бать, Г. Ю. Джанелидзе, А. С. Кельзон. – 9-е изд., стер. – СПб : Издательство «Лань», 2010. – 640 с.

3 Яблонский, А. А. Курс теоретической механики: учебник /А. А. Яблонский, В. М. Никифорова. – 9-е изд., стер. – СПб., Издательство «Лань», 2004. – 768 с.

4 Бутенин, Н. В. Курс теоретической механики. В 2-х томах / Н. В. Бутенин, Я. Л. Лунц, Д. Р. Меркин. – 11-е изд., стер. – СПб. : Издательство «Лань», 2009. – 736 с.

Оглавление

Краткие сведения из теории……………………………………………. 3

Пример выполнения задания…………………………………………… 7

Таблица 1– Исходные данные………………………………………… . 15

Таблица 2 – Расчетные схемы механизмов……………………… 16

Библиографический список…………………………………………… 21

Учебное издание

Сидашов Андрей Вячеславович

Василькова Елена Андреевна

Жукова Юлия Викторовна

ПРИМЕНЕНИЕ ОБЩЕГО УРАВНЕНИЯ ДИНАМИКИ

И УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА ПРИ ИССЛЕДОВАНИИ ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ

Учебно-методическое пособие

к расчетно-графической работе по теоретической механике

Редактор Н. С. Федорова

Корректор Н. С. Федорова

Подписано в печать 28.12.2011. Формат 60×84/16.

Бумага газетная. Ризография. Усл. печ. л. 1,27.

Уч.-изд. л. 1,16. Тираж 101 экз. Изд. № 103. Заказ №6192

Ростовский государственный университет путей сообщения.

Ризография РГУПС.

 

Адрес университета: 344038, Ростов н/Д, пл. Ростовского Стрелкового

Полка Народного Ополчения, 2.