Дифракционная решетка, освещенная нормально падающим монохрома­тическим светом

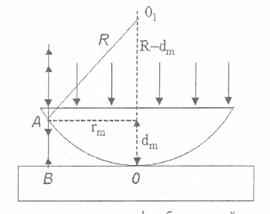
Рис.8

Поскольку по условию задачи d необходимо найти в том месте, где наблюдается светлое кольцо, то dx следует приравнять ml:

dx = 2 АВп + l/2 = ml, (2)

— условие усиления света.

Из (2) найдем AВ = d:

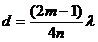
Подставляя в (3) числовые значения величин и произведя вычисления, найдем:

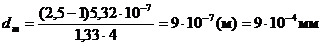
Ответ: dm= — 9 .10-4мм = 0,9 мкм.

Пример 4

Дифракционная решетка, освещенная нормально падающим монохрома­тическим светом, отклоняет спектр третьего порядка на угол j1 = 10°30′. На какой угол j2, отклоняет она спектр пятого порядка?

Дано:

m1, = 3;

m2=5;

φ1= 10°30′

φ2 = ?

Решение

На основании формулы дифракционной решетки напишем выражение синуса угла отклонения спектра третьего и пятого порядков дифракционного максимума:

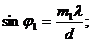(1)

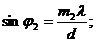(2)

где d— период решетки;

φ—угол, между направлением на дифракционный максимум и норма­лью к решетке;

l—-длина волны монохроматического света.

Найдя l! d из (1) и подставив его значения в (2),получим:

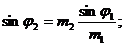
Подставляя в формулу (3) числовые значения, получим:

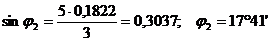
Ответ: на угол φ2= 17°41′.

Пример 5

Как изменится энергетическая светимость абсолютно черного тела, если максимум лучеиспускательной способности его переместится от красной гра­ницы видимого света (760 нм) к его фиолетовой границе (380 нм)?

Дано:

l01 = 760 нм = 7,6 . 10-7м;

l02 = 380 нм = 3,8 . 10-7м

s = 5,67 . 10-8 Дж/(м2 . с . К4).

RОэ2/ RОэ1=?

Решение

Энергетическую светимость абсолютно черного тела можно найти из за­кона Стефана-Больцмана:

RОэ=sТ4 (1)

где s — постоянная Стефана-Больцмана;

Т — абсолютная температура тела.

Температуру тела можно найти из первого закона Вина:

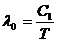(2)

где l0 — длина волны, которой соответствует максимальное значение лу­чеиспускательной способности абсолютного черного тела. По условию задачи l0 изменяется от 760 до 380 нм, что соответствует изменению температуры тела от Т1 до Т2 Найдем и Т2 из (2):

Т1=C1/l01; Т2=C2/l02 (3)

Подставляя (3) в (1) получим:

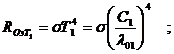(4)

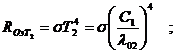(5)

Разделив (5) на (4), получим:

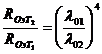
Подставляя в (6) числовые значения величин и производя вычисления, найдем

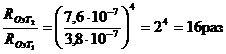
Пример 6

При поочередном освещении поверхности некоторого металла светом с дли­нами волны l1= 0,35 мкм и l2 = 0,54 мкм обнаружили, что соответствующие максимальные скорости фотоэлектронов отличаются друг от друга в k = 2,0 раза. Найти работу выхода электрона с поверхности этого металла.

Дано:

l1 = 0,35 мкм = 3,5 .10-7м;

l2 = 0,54 мкм = 5,4 .10-7м;

k = ?

A =?

Решение

Для решения задачи воспользуемся уравнением Эйнштейна для фотоэффекта:

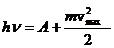(1)

Так как υ=c/l, то уравнение (1) запишем как:

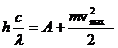(2)

При освещении металла светом с длиной волны l1 уравнение (2) примет вид:

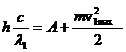(3)

При освещении металла светом с длиной волны l2 уравнение (2) примет вид:

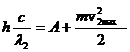(4)

Поскольку, l1 < l2 то, как это следует из уравнения Эйнштейна, υ1, больше υ2 по условию задачи υ1=2υ2 и,. Если υ1 в 2 раза больше υ2, то Wкин1, в 4 раза больше Wкин2. Тогда уравнения (3) и (4) можно записать так:

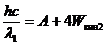; (5)

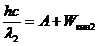(6)

Умножим (6) на (4) и вычтем из него (5):

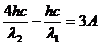(7)

Найдем из (7):

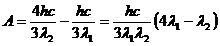(8)

Подставляя в (8) числовые значения величин и произведя вычисления, получим:

.

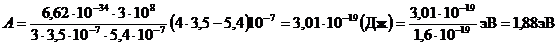Ответ: А = 3,01·10 -19 Дж = 1,88 эВ

Пример 7

Определить массу частицы, кинетическая энергия которой 100 эВ, а длина волны де Бройля 1,00·10 -10 см.

Дано:

Wкин = 200 эВ = 200·1,6·10-19 Дж;

lБ = 1,00·10-10см= 1,00·10-12 м;

h = 6.62·10-34 Дж·с.

т = ?

Решение

Длина волны де Бройля для частицы зависит от ее импульса р и определяется формулой:

lБ = h/р, (1)

Импульс частицы можно определить, если известна ее кинетическая энергия:

.

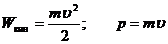Откуда

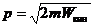. (2)

Подставим (2) в (1):

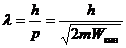, (3)

откуда

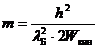. (4)

Подставляя численные значения величин и произведя вычисления, получим

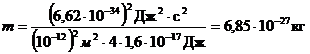
Ответ: т = 6,85·10-27 кг.

Пример 8

Электрон в атоме водорода перешел с третьего энергетического уровня на первый. Сколько линий появится в спектре атомов водорода и какова их длина волны?

Дано:

ni = 3; l1 = ?

nf = 1; l2 = ?

R =1,097·107 l/м. l3 = ?

Решение

Для определения l воспользуемся сериальной формулой Бальмера:

.

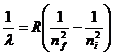Нарисуем энергетический спектр атома водорода. Он представляет собой систему горизонтальных линий, расстояние между которыми уменьшается с увеличением номера уровня (рис. 9). Электрон из состояния пi = 3 может перейти либо сразу в состояние nf= 1, либо сначала в состояние с пf= 2, а затем в состояние пf = I; поэтому в спектре будут наблюдаться три линии.

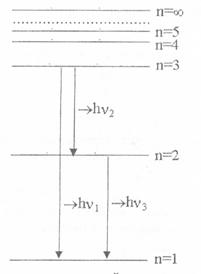
Рис. 9

Найдем длины волн этих линий:

; (2)