Дифракция френеля на круглом отверстии

так как выражения, стоящие в скобках, согласно (3-5), равны нулю, а оставша­яся часть от амплитуды последней зоны ±Аm/2 ничтожно мала.

Таким образом, амплитуда, создавае­мая в произвольной точке М сферической волновой поверхностью, равна половине амплитуды, создаваемой одной централь­ной зоной. Следовательно, действие всей волновой поверхности на точку М сводит­ся к действию ее малого участка, меньше­го центральной зоны.

Если в выражении (3-2) положим, что высота сегмента hm<<а (при не слиш­ком больших m), тогда 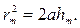Под­ставив сюда значение (3-3), найдем ра­диус внешней границы m-й зоны Френеля:

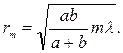(3-7)

При a=b=10 см и l=0,5 мкм радиус центральной зоны r1= 0,158 мм. Следовательно, распростра­нение света к точке М происходит так, будто световой поток распространяется внутри очень узкого канала вдоль SM, т. е. прямолинейно. Таким образом, принцип Гюйгенса — Френеля позволяет объяснить прямолинейное распростране­ние света.

Правомерность деления волнового фронта на зоны Френеля подтверждена экспериментально с использованием зонных пластинок — стеклянных пластинок, состоящих из прозрачных и не­прозрачных концентрических колец, по­строенных по принципу расположения зон Френеля, т. е. с радиусами rm зон Френеля, определяемыми выражением (3-7) для заданных значений a, b и l (m = 0, 2, 4, … для прозрачных и m = 1, 3, 5, … для непрозрачных колец). Если поместить зон­ную пластинку на расстоянии а от то­чечного источника и на расстоянии b от точки наблюдения на линии, соединяющей эти две точки, то для света длиной волны l она перекроет четные зоны и оставит сво­бодными нечетные начиная с центральной. Результирующая ам­плитуда A=А1+А3+А5+… должна быть больше, чем при полностью открытом фронте. На опыте зонная пластинка во много раз увеличивает ин­тенсивность света в точке М, действуя подобно собирающей линзе.

3.3. Дифракция Френеля на круглом отверстии

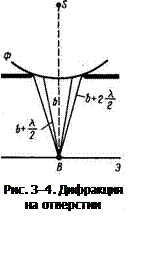Сферическая волна, идущая из точечного источника S, встречает на своем пути экран с круглым отверстием. Дифракционная картина наблюдается на экране (Э) в точке В, лежащей на линии, соединяющей источник S с центром отверстия. Экран параллелен плоскости отвер­стия и находится от него на расстоянии b (рис. 3-4). Разобьем открытую часть волновой по­верхности Ф на зоны Френеля. Вид диф­ракционной картины зависит от числа зон Френеля, укладывающихся в отверстии. Амплитуда результирующего колебания, возбуждаемого в точке В всеми зонами (см. (3-1) и (3-6)),

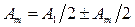, (3-8)

где знак плюс соответствует нечетным m, а знак минус — четным.

Если отверстие открывает нечетное число зон Френеля, то амплитуда в точке В будет больше, чем при свободном распространении волны, если четное, то амплитуда бу­дет равна нулю. Если в отверстие уклады­вается одна зона Френеля, то в точке В амплитуда A=А1, т. е. вдвое больше, чем в отсутствие непрозрачного экрана с отверстием. Интенсивность света больше соответственно в четыре ра­за. Если в отверстии укладываются две зоны Френеля, то из-за интерференции их действия в точке В практически уничтожат друг друга. Таким образом, дифрак­ционная картина от круглого отверстия вблизи точки S будет иметь вид чередую­щихся темных и светлых колец с центрами в точке В (если m четное, то в центре будет темное кольцо, если m нечетное — то светлое кольцо), а интенсивность максимумов убывает с расстоянием от центра картины. Если отверстие освещается бе­лым светом, то кольца будут окрашены.

Число зон Френеля, укладывающихся в отверстии, зависит от его диаметра. Если он большой, то Аm<<А1 и результирующая амплитуда А=А1/2, т. е. такая же, как и при полностью открытом волновом фрон­те. При этом дифракционной картины нет — свет распространяется, как и в отсутствие круглого отверстия, прямо­линейно.

3.4. Дифракция Френеля на диске

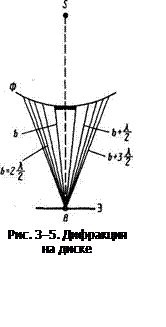
Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск. Дифракционную картину наблюдаем на экране (Э) в точке В, лежащей на линии, соединяющей S с центром диска. Закрытый диском участок фронта волны надо исклю­чить из рассмотрения и зоны Френеля строить начиная с краев диска (рис. 3-5). Пусть диск закрывает m зон Френеля. Амплитуда результирующего колебания в точке В равна

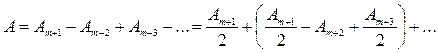или

А=Аm+1/2, так как выражения, стоящие в скобках, равны нулю. Следовательно, в точке В будет всегда наблюдаться интерференционный максимум (светлое пятно), соответствую­щий половине действия первой открытой зоны Френеля. Центральный максимум ок­ружен концентрическими с ним темными и светлыми кольцами, а интенсивность максимумов убывает с расстоянием от центра картины.

С увеличением радиуса диска первая открытая зона Френеля удаляется от точ­ки В и увеличивается угол jm (см. рис. 3-3) между нормалью к поверхности этой зоны и направлением на точку В. В ре­зультате интенсивность центрального мак­симума с увеличением размеров диска уменьшается. При больших размерах диска за ним наблюдается тень, вблизи границ которой имеет место слабая дифракционная картина. В данном случае дифракцией света можно пренебречь и считать свет распространяющимся пря­молинейно.

Отметим, что дифракция на круглом от­верстии и дифракция на диске впервые рассмотрены Френелем.

3.5. Дифракция Фраунгофера на одной щели

Немецкий физик И. Фраунгофер (1787— 1826) рассмотрел дифракцию плоских све­товых волн, или дифракцию в параллель­ных лучах. Дифракция Фраунгофера наблюдается в том случае, когда источник света и точка наблюдения бесконечно уда­лены от препятствия, вызвавшего диф­ракцию. Для этого достаточно точечный источник света поместить в фокусе собирающей линзы, а дифракционную картину иссле­довать в фокальной плоскости второй со­бирающей линзы, установленной за препятствием.

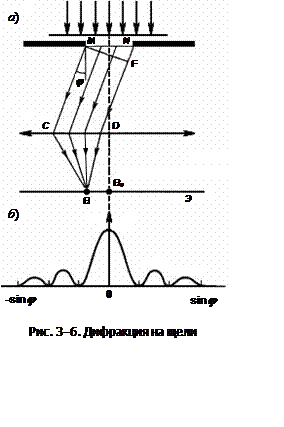
Рассмотрим дифракцию Фраунгофера от бесконечно длинной щели (для этого практически достаточно, чтобы длина ще­ли была значительно больше ее ширины). Пусть плоская монохроматическая свето­вая волна падает нормально плоскости узкой щели шириной MN = а (рис. 3-6, а). Опти­ческая разность хода между крайними лучами МС и ND, идущими от щели в произвольном направлении j,

,

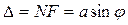где F — основание перпендикуляра, опу­щенного из точки М на луч ND.

Разобьем часть волновой поверхности в плоскости щели MN на зоны Френеля в виде полос, параллель­ных ребру М щели. Ширина каждой зоны выбирается таким образом, чтобы разность хода от краев этих зон была равна l/2. На ширине щели тогда уместится 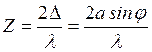зон. (3-8)

Если свет на щель падает нормально, то плоскость щели совпадает с фронтом волны и все точки фронта в плоскости щели будут колебаться в одной фазе. Амплитуды вторичных волн в плоскости щели будут равны, т. к. выбранные зоны Френеля будут иметь равные площади и одинаковый наклон к направлению наблюдения.

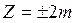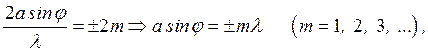Как следует из (3-8), число зон Френеля, укладывающихся на ширине щели, зависит от угла j и определяет ре­зультат наложения всех вторичных волн. При интерференции колебания от каждой пары соседних зон взаимно погашают друг друга, следова­тельно, если число зон Френеля четное, т. е. , то (3-9)

где m – натуральный ряд чисел, m = 1, 2, 3, … .

Таким образом в точке В наблюдается дифракционный минимум (полная темнота) первого, второго, третьего и т. д. порядков.

Если число зон Френеля нечетное, т. е. 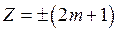, то 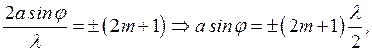(3-10)

где m – натуральный ряд чисел, m = 0, 1, 2, 3, … и наблюдается дифракционный максимум нулевого, первого, второго, третьего и т. д. порядков, соответствующий действию одной некомпенсированной зоны Френеля.

В прямом направлении (j = 0) щель действует как одна зона Френеля, и свет распространя­ется с наибольшей интенсивностью, т. е. в точке В0 наблюдается центральный дифракционный максимум.

Распределение ин­тенсивности (дифракционный спектр), получаемое из-за дифракции, приведено на рис. 3-6, б. Положение дифракционных максиму­мов зависит от длины волны l, поэтому такой вид дифракционная карти­на имеет лишь для монохроматического света. При освещении щели белым светом центральный максимум имеет вид белой полоски; он общий для всех длин волн (при j = 0 разность хода равна нулю для всех l).