Дифракция на круглом отверстии и на круглом экране
Задача 1. Интенсивность плоской электромагнитной волны, распространяющейся в пространстве без препятствий, равна I0. На пути волны поставили непрозрачный экран с прямолинейным краем, параллельный волновым поверхностям. Чему равна интенсивность волны на границе геометрической тени экрана?
Указание. При ответе на поставленный в задаче вопрос пользуйтесь рисунками 49 и 50. Учтите, что загораживание экраном части волнового фронта приводит к убиранию из спирали соответствующей части векторочков.
Задача 2. Используя рисунок 49, дайте качественное объяснение зависимости интенсивности электромагнитной волны от расстояния до границы геометрической тени экрана, изображенной на рисунке 47. Попытайтесь объяснить, почему при перемещении вглубь тени от экрана колебаний интенсивности не происходит.
Указание. Перемещение вдаль от края геометрической тени в освещенную область равносильно включению все новых антенн, которые ранее были закрыты экраном. Перемещение от края тени в затененную область равносильно выключению антенн.
2.1.4 Зоны Френеля
При решении задачи 2 обращает внимание на себя следующий факт. При получении результирующей напряженности электрического поля волны путем последовательного сложения бесконечно малых вкладов приращения напряженности оказываются то положительными, то отрицательными.
Участок фронта волны, все части которого дают вклады в результирующую напряженность в данной точке наблюдения одного знака, называется зоной Френеля.
На рисунке 50 отмечены половина первой, вторая и третья зоны вкладов одного знака.
Задача 3. На рисунке 47 изображена зависимость интенсивности электромагнитной волны от расстояния до границы геометрической тени экрана. Отметьте на этой зависимости участки, являющиеся результатом добавок 1й, 2й, 3й и 4й зон Френеля одного знака.
Вопрос 2. На пути электромагнитной волны поставили полосатый экран: непрозрачные участки загораживают четные зоны, а прозрачные участки приходятся на нечетные зоны. К какому эффекту это приведет? Изобразите диаграмму сложения вкладов в электрическое поле волны от элементарных источников.
3. Дифракция на круглом отверстии и на круглом экране
3.1 Поправка к определению зон Френеля для плоской волны
Выбор участков фронта волны в виде прямых полосок не вполне соответствует определению зоны Френеля, данному в разделе 2.1.4, так как на каждой из полосок имеются чередующиеся участки, дающие вклады в электрическое поле противоположного знака.
Вопрос 3. Какую форму должны иметь зоны Френеля плоской волны для заданной точки P?
Границы зон выбираются таким образом, чтобы разность хода вторичных волн, пришедших от краев, равнялась половине длины волны.
Задача 4. Плоская электромагнитная волна, излучаемая генератором трехсантиметровых волн, принимается в точке P, находящейся на расстоянии L от выбранного фронта. Рассчитать радиус первой зоны Френеля на волновом фронте, отстоящем от точки P на расстоянии L=1,5 м.
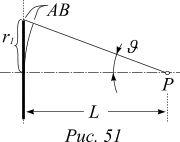 Решение. На рисунке изображено расположение фронта, точки P и границы первой зоны (зона помечена жирной линией). По определению, разность хода AB от точки О и от границы первой зоны Френеля должна равняться половине длины волны, т. е.
Решение. На рисунке изображено расположение фронта, точки P и границы первой зоны (зона помечена жирной линией). По определению, разность хода AB от точки О и от границы первой зоны Френеля должна равняться половине длины волны, т. е.
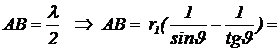 ,
,
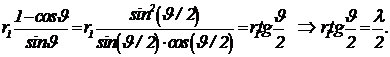 (1)
(1)
где J — угол, под которым виден радиус первой зоны. При малых углах 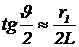 . Так что уравнение (1) дает
. Так что уравнение (1) дает
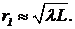 (2)
(2)
Подставляя данные условия задачи, находим r1»21 см.
Задача 5. Используя условия задачи 4, рассчитайте размеры следующих трех зон Френеля.
3.2 Зоны Френеля на сферическом фронте
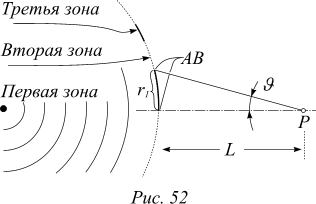 Если электромагнитная волна генерируется точечным колеблющимся зарядом, расположенным не слишком далеко от точки наблюдения P, то при расчете дифракционной картины при прохождении волной препятствия или отверстия надо иметь в виду, что волновой фронт является сферой. Зоны Френеля следует определять на этой сфере (рисунок 52). При этом, за исключением геометрических построений, вся идея расчета дифракционной картины остается той же самой, что и в случае плоской волны.
Если электромагнитная волна генерируется точечным колеблющимся зарядом, расположенным не слишком далеко от точки наблюдения P, то при расчете дифракционной картины при прохождении волной препятствия или отверстия надо иметь в виду, что волновой фронт является сферой. Зоны Френеля следует определять на этой сфере (рисунок 52). При этом, за исключением геометрических построений, вся идея расчета дифракционной картины остается той же самой, что и в случае плоской волны.
[См. также учебник “Физика 11” под ред. А. А.Пинского §34.]
Задача 6. Экран с круглым отверстием радиусом 1,5 мм расположен на расстоянии 8,6 м от точечного источника света, излучающего свет с длиной волны 0,6 мкм. Источник находится на оси отверстия. На каком расстоянии от отверстия расположена точка наблюдения, если из нее видна одна первая зона Френеля?
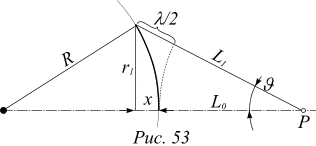 Решение. При решении данной задачи проведем уже известный из предыдущего рассмотрения дифракции плоской волны ход рассуждений, восстановим чертеж и еще раз разберемся в геометрии первой зоны Френеля.
Решение. При решении данной задачи проведем уже известный из предыдущего рассмотрения дифракции плоской волны ход рассуждений, восстановим чертеж и еще раз разберемся в геометрии первой зоны Френеля.
Из чертежа на рисунке 53 для радиуса r1 имеем: 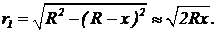 (3)
(3)
Разность хода волны от центра зоны и от края первой зоны равна 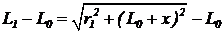 . (4)
. (4)
При r1, x<<L0 для этой разности имеем 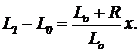 (5)
(5)
Из определения границы первой зоны L1-Lo=l/2 определяем высоту x 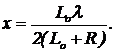 (6)
(6)
Соответственно подстановка (6) в (3) позволяет найти искомое расстояние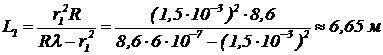 . (7)
. (7)
Вопрос 4. Точка P находится от фронта волны на расстоянии L. В какой ситуации размеры зон Френеля больше — при плоском фронте или сферическом?
Задача 7. В опытах с сантиметровыми волнами (длина волны 3,2 см) рупорные антенны генератора и приемника располагаются на одной прямой на расстоянии 1,2 м друг от друга. Посередине между ними располагается металлический экран с диафрагмой, раствор которой можно плавно изменять. При плавном раскрытии диафрагмы сигнал вначале усиливается, затем убывает, затем снова усиливается и вновь убывает. Определите радиусы раскрытия диафрагмы во всех четырех случаях — два максимума и два минимума сигнала.
4. Домашнее задание
4.2 Решение задач
Задача 1. На какое расстояние (вдоль центрального луча) надо переместить точку наблюдения (см. задачу 6), чтобы в ней образовалось темное пятно (интерференционный минимум)?
Задача 2. Параллельный пучок света падает нормально на круглую диафрагму радиусом 1,4 мм, расположенную на расстоянии 4 м от точки наблюдения. Что будет в точке наблюдения — светлое или темное пятно? Длина световой волны 0,5 мкм.
Задача 3. Расширяя диафрагму (см. задачу 2 домашнего задания), мы увидим, что освещенность в точке наблюдения уменьшается. Не противоречит ли это закону сохранения энергии? При каком радиусе диафрагмы точка наблюдения попадет в темное пятно? Куда делась энергия?
занятие 1.2.5
дифракция. решение задаЧ
1.1 Контрольные вопросы
1.1.1 Почему, используя различные диафрагмы, невозможно получить как угодно тонкий луч света?
1.1.2 В чем состоит принцип Гюйгенса-Френеля?
1.1.3 Используя законы электродинамики, дайте качественное обоснование принципу Гюйгенса-Френеля.
1.1.4 Почему при прохождении света через щель, толщина которой меньше длины волны, происходит монотонное распределение засветки регистрирующего экрана, а при прохождении света через щель, толщина которой составляет несколько длин волн, наблюдаются интерференционые эффекты?
1.1.5 Что такое зона Френеля?
1.1.6 При каких условиях в центре тени от круглого диска возникает светлое пятно (пятно Пуассона)?
1.1.7 Чем будут отличаться дифракционные картины от дифракционных решеток с одинаковыми плотностями штрихов, но если одна решетка содержит много штрихов, а другая — мало (несколько штук)?
1.2 обсуждение задач домашнего задания
2. Решение задач
2.1 Дифракция на круглом отверстии
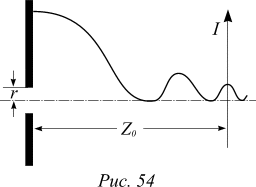 Задача 1 [C12.2.7]. На отверстие радиуса r падает перпендикулярно его плоскости плоская синусоидальная волна. Интенсивность волны вдоль оси отверстия периодически изменяется. На каком расстоянии от его центра находится последний максимум? Определите расстояние между максимумами интенсивности на расстоянии zo от центра отверстия, если
Задача 1 [C12.2.7]. На отверстие радиуса r падает перпендикулярно его плоскости плоская синусоидальная волна. Интенсивность волны вдоль оси отверстия периодически изменяется. На каком расстоянии от его центра находится последний максимум? Определите расстояние между максимумами интенсивности на расстоянии zo от центра отверстия, если 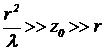 .
.


