задачи по электродинамике

Задача №362.

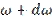Две частицы с массами m1 и m2 и одноименными зарядами e1 и е2 двигаются по прямой из бесконечности навстречу друг другу. Когда взаимное расстояние становится равным l, частицы останавливаются, после чего совершают движение в противоположном направлении, разлетаясь на бесконечность. Определить энергию дипольного излучения, приходящуюся на интервал частот от до . Исследовать полученное выражение в области малых и больших частот.

Переходим в систему центра масс, строим ось X вдоль этой прямой по которой частицы друг к другу движутся и направляем на встречу частицы с приведенной массой 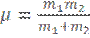. Эта (условная) частица с приведенной массой летит к центру кулоновского поля отталкивания. Ну и подчиняется закону Ньютона:

Так как частицы остановились на расстоянии друг от друга l, то же самое с приведенной частицей будет и у нас, ну и конечно удобно этот момент принять за начало отсчета времени .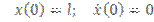

Дипольный момент можно определить вот так вот. 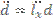Учитывая, что у нас все вообще одномерное, то векторы, то становятся скалярами. И тогда вторая производную дипольного момента можно записать как: 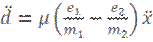Учитывая закон Ньютона: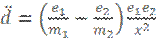

Согласно формуле IV.20 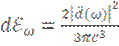(дипольное приближение) нам надо выразить вторую производную дипольного момента через частоту излучения, которое этот диполь излучает. Чтоб сделать это надо взять интеграл. 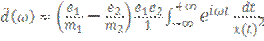Где x зависит от времени тоже, а экспонента в интеграле собственно и отражает зависимость от частоты.

Чтоб взять этот интеграл перейдем к новой переменной 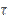по формулам,

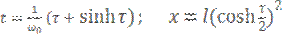при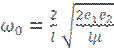

Такой переход учитывает зависимость координаты от времени как движение частицы с массой 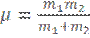, начальным расстоянием l и силой отталкивания .

В результате замены получим: 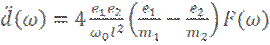где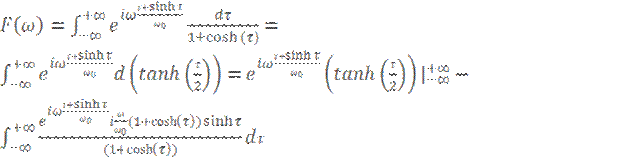

Берем этот интеграл по частям. Учитывая, что

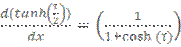и 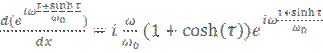затем делаем замену 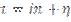получим:

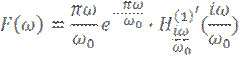
Где 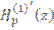функция Ганкеля, от аргумента и параметра так как функция Ганкеля определяется следующим образом

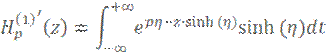
В таком случае: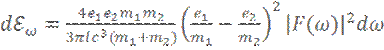

Рассматривая два предельных случая соотношения частот получим.

1) 

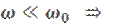
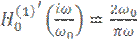
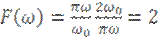
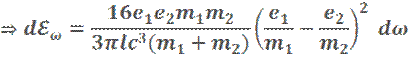
2)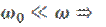
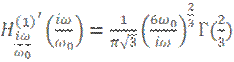
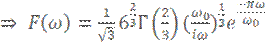