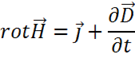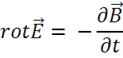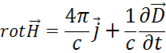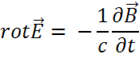лекция по электродинамике
Введение
План
I. Предмет и метод электродинамики. Представления о поле и веществе
в электродинамике.
II. Краткая история развития электродинамики.
III. Концепции близко и дальнодействия.
I. Электродинамика — раздел теоретической физики, изучающий свойства электромагнитного поля и взаимодействие поля с веществом. Электродинамика — фундаментальная физическая наука. Без открытий электродинамики, внедренных в практику человеческой деятельности, существование современной цивилизации невозможно. Это производство и потребление электроэнергии, это связь, обусловленная применением электромагнитных волн, это радио и телевидение, электротранспорт и многое другое, что обусловило невиданный
в истории человечества научно-технический прогресс XX века.
Изучение электродинамики способствует формированию современной научной картины мира.
Неслучайно поэтому электродинамика составляет примерно третью часть
школьного курса физики.
В основе электродинамики лежат представления о поле и веществе. Отметим – в дальнейшем мы часто будем просто говорить "поле", опуская "электромагнитное". Электромагнитно поле — вид материи, который характеризуется такими же физическими величинами, как и вещество — энергия, импульс, масса. Но имеет и свои специфические характеристики — векторы напряженности и индукции, потенциалы. Наглядно представить себе поле сложно, но, по словам Ландау, "мы можем понять даже то, что себе вообразить не можем". И это одна из основных задач курса электродинамики.
Электромагнитное поле оказывает силовое воздействие на заряженные тела. В вакууме поле распространяется со скоростью 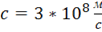 . В классическом представлении поле непрерывно. Однако уже в 1905 г. Эйнштейн ввел представление о дискретном распределении поля в виде квантов — фотонов, но в классической электродинамике, к изучению которой мы приступаем, эти представления не используются, они используются в квантовой электродинамике. Необходимо особо отметить, что электромагнитное поле не имеет электрического заряда. Электрический заряд — свойство вещества. Наименьший электрический заряд — это заряд электрона
. В классическом представлении поле непрерывно. Однако уже в 1905 г. Эйнштейн ввел представление о дискретном распределении поля в виде квантов — фотонов, но в классической электродинамике, к изучению которой мы приступаем, эти представления не используются, они используются в квантовой электродинамике. Необходимо особо отметить, что электромагнитное поле не имеет электрического заряда. Электрический заряд — свойство вещества. Наименьший электрический заряд — это заряд электрона 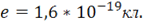
В классической электродинамике используются различные представления
о веществе. Вещество трактуется как непрерывная среда — это макроскопическая или феноменологическая электродинамика. Учет дискретности вещества проводится в микроскопической электродинамике.
В макроскопической электродинамике поле характеризуется четырьмя векторами: 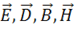 . Первые два – электрическая напряженность и электрическая индукция, вторая пара – магнитная индукция и магнитная напряженность. Вещество описывается физическими величинами: ℰ – диэлектрическая проницаемость, µ – магнитная проницаемость, 𝜆 – электропроводность, а так же зарядом q, ρ – объемная плотность распределения заряда, σ – поверхностная плотность заряда.
. Первые два – электрическая напряженность и электрическая индукция, вторая пара – магнитная индукция и магнитная напряженность. Вещество описывается физическими величинами: ℰ – диэлектрическая проницаемость, µ – магнитная проницаемость, 𝜆 – электропроводность, а так же зарядом q, ρ – объемная плотность распределения заряда, σ – поверхностная плотность заряда.
В основе макроскопической электродинамики лежит система четырех уравнений Максвелла.
В микроскопической электродинамике поле описывается двумя векторами: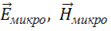 — микроскопические (иногда говорят "истинные") электрическая и магнитная напряженности. Вещество описывается элементарным зарядом е, концентрацией зарядов n, массой заряженной частицы m, скоростью
— микроскопические (иногда говорят "истинные") электрическая и магнитная напряженности. Вещество описывается элементарным зарядом е, концентрацией зарядов n, массой заряженной частицы m, скоростью ![]() . Четыре уравнения Максвелла-Лоренца – основа микроскопической электродинамики.
. Четыре уравнения Максвелла-Лоренца – основа микроскопической электродинамики.
II. В истории развития электродинамики условно можно выделить три основных этапа.
1) Накопление экспериментальных фактов, открытие экспериментальных законов. Этот этап начинается, конечно, с открытия закона Кулона. Но, главное, с опубликования в 1820 году опыта Эрстеда. Опыты Эрстеда означали, что вокруг проводника с током появляется магнитное поле! Затем наступил, как отмечает В. Карцев [], «звездный час Ампера». Ампер ввел в физику термин "электродинамика", открыл закон – закон Ампера, силу – силу Ампера и т. п. Затем в течение первого года последовало установление закона Био-Савара и его математическое оформление Лапласом, наконец, в 1831 году — открытие Фарадеем явления электромагнитной индукции, увенчавшим его идею "превратить магнетизм в электричество". После этого наступил основной этап.
2) Создание теории электромагнитного поля, связанное с именем Максвелла. Кратко отметим основные результаты работ Максвелла:
1. Максвелл обобщил всю совокупность экспериментальных фактов, накопленных к тому времени, создав теорию электромагнитного поля.
2. Впервые в истории теоретической физики создал теорию, объединяющую
взаимодействия — электрическое и магнитное — в электромагнитное.
Это особенно актуально в настоящее время, когда делаются попытки создания теории, объединяющей все четыре фундаментальных взаимодействия.
3. Теоретически — "на кончике пера" — предсказал существование электромагнитных волн в природе, теоретически доказал, что свет есть электромагнитные волны.
Позднее в 1905 году Эйнштейн показал, что электромагнитное поле не нуждается ни в каком материальном носителе — эфире, оно само является видом материи, причем разделение на электрическое и магнитное поле условно, связано с выбором системы отсчета. Кроме того ввел представление о квантовом характере электромагнитного поля.
3) Экспериментальное подтверждение, внедрение.
Здесь необходимо отметить работы Герца по экспериментальному — в физической лаборатории — созданию электромагнитных волн и изучению их свойств. А затем изобретение радио А. С.Поповым и продолжающееся и поныне внедрение в практику человеческой деятельности результатов электродинамики, которые трудно переоценить.
В последующих лекциях будут приводиться некоторые исторические справки установления определенных законов и следствий электродинамики.
III. В физике используются две концепции, которые по-разному трактуют взаимодействие материальных объектов. Это концепции близко и дальнодействия. Рассмотрим, например, взаимодействие двух
заряженных тел с зарядами  , находящимися на расстоянии
, находящимися на расстоянии ![]()
друг от друга (см. Рис. I.)

![]()
![]() Рис. I. Два заряженных тела
Рис. I. Два заряженных тела
![]()
![]()
![]()
Концепция дальнодействия: взаимодействие происходит мгновенно, время взаимодействия 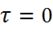 . Это означает, что скорость взаимодействия бесконечна. Взаимодействие происходит на любом расстоянии, и никакого переносчика взаимодействия нет. При этом причина и следствие находятся в разных
. Это означает, что скорость взаимодействия бесконечна. Взаимодействие происходит на любом расстоянии, и никакого переносчика взаимодействия нет. При этом причина и следствие находятся в разных
точках пространства. Формально применяется интегральная формa описания взаимодействия. Эта концепция приводит к большим трудностям. В самом
деле, представим себе, что расположенное в какой-то точке заряженное тело с зарядом ![]() перемешается в некоторую сторону, вправо, например. (см. Рис. 2)
перемешается в некоторую сторону, вправо, например. (см. Рис. 2)
![]()

![]() Рис. 2. Перемещение заряженного тела
Рис. 2. Перемещение заряженного тела
![]()

А где же искать причину? По закону Кулона это должен быть заряд ![]() ,
,
который либо притягивает, либо отталкивает заряд ![]() (зависит от знаков
(зависит от знаков ![]() и
и![]() ), но находится на одной прямой с вектором
), но находится на одной прямой с вектором ![]() . Но может быть и несколько разных зарядов, расположенных в различных точках пространства, которые дают тот же эффект. В принципе придется учитывать заряды во всей Вселенной. Как видите, это весьма неблагодарная задача. Оговорка? В дальнейшем везде используется научный жаргон — для краткости будем говорить "заряд" вместо "заряженная частица" или "заряженное тело".
. Но может быть и несколько разных зарядов, расположенных в различных точках пространства, которые дают тот же эффект. В принципе придется учитывать заряды во всей Вселенной. Как видите, это весьма неблагодарная задача. Оговорка? В дальнейшем везде используется научный жаргон — для краткости будем говорить "заряд" вместо "заряженная частица" или "заряженное тело".
Концепция близкодействия: взаимодействие осуществляется за конечное
время, т. е.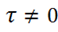 . Скорость взаимодействия конечна. Предельной скоростью
. Скорость взаимодействия конечна. Предельной скоростью
физического взаимодействия согласно специальной теории относительности
является скорость света в вакууме. При этом материальным носителем взаимодействия является поле, в данном случае электромагнитное. Причина (состояние поля в данной точке) и следствие — сила, действующая на заряд ![]() , находятся в одной и той же точке пространства (или в бесконечно близких точках) — отсюда название концепции — близкодействие. Можно представить себе, как происходит взаимодействие: заряд
, находятся в одной и той же точке пространства (или в бесконечно близких точках) — отсюда название концепции — близкодействие. Можно представить себе, как происходит взаимодействие: заряд ![]() создает поле, но это состояние поля доходит до места, где находится
создает поле, но это состояние поля доходит до места, где находится ![]() не мгновенно, а через некоторое время и тогда только подействует с некоторой силой на
не мгновенно, а через некоторое время и тогда только подействует с некоторой силой на ![]() ! Для того чтобы определить эту силу, надо знать характеристику поля в том же месте, где находится наш "подопытный" заряд
! Для того чтобы определить эту силу, надо знать характеристику поля в том же месте, где находится наш "подопытный" заряд ![]() . В этом огромное преимущество концепции близкодействия. Существенно, что в этой концепции вводится представление о поле, как о переносчике взаимодействия. Для описания физических явлений применяется дифференциальная форма. Поэтому в электродинамике появляются уравнения в дифференциальной форме.
. В этом огромное преимущество концепции близкодействия. Существенно, что в этой концепции вводится представление о поле, как о переносчике взаимодействия. Для описания физических явлений применяется дифференциальная форма. Поэтому в электродинамике появляются уравнения в дифференциальной форме.
Современная теоретическая физика использует концепцию близкодействия. Математическим аппаратом электродинамики является векторный анализ, основы которого изучаются либо в курсе высшей математики, либо в курсе "Методы математическое физики" (см. Приложение 1).
Глава I. ОCHOBЫ МАКРОСКОПИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ
В этой главе будут рассмотрены: система уравнений Максвелла как обобщение экспериментальных законов, закон сохранения и превращения энергии
электромагнитного поля, граничные условия для нормальных и касательных
составляющих векторов электромагнитного поля.
§I. Четвертое уравнение Максвелла как обобщение экспериментального закона Кулона
План:
I. Полевая трактовка закона Кулона. Напряженность и индукция поля
точечного заряда.
II. 2-я (электростатическая) теорема Остроградского-Гаусса.
III. 4-е уравнение Максвелла как обобщение закона Кулона.
1. Закон Кулона — закон взаимодействия неподвижных точечных зарядов.
Точечный заряд — это абстракция. Точечным зарядом можно считать заряд тела, размерами которого можно пренебречь или, например, размеры взаимодействующих заряженных тел достаточно малы по сравнению с расстоянием между ними.
Рассмотрим два точечных заряда ![]() и
и ![]() , находящихся на расстоянии
, находящихся на расстоянии ![]() (рис. 3).
(рис. 3).
 рис 3. Два точечных заряда.
рис 3. Два точечных заряда.
Сила, действующая на ![]() , по закону Кулона равна:
, по закону Кулона равна:
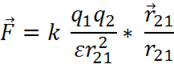
![]() — коэффициент пропорциональности, зависящий от выбора системы единиц.
— коэффициент пропорциональности, зависящий от выбора системы единиц.
В СИ: 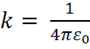 , где
, где ![]() — диэлектрическая проницаемость вакуума.
— диэлектрическая проницаемость вакуума.
В гауссовой системе 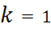 . В дальнейшем используется гауссова система единиц – для преемственности с другими разделами теоретической физики.
. В дальнейшем используется гауссова система единиц – для преемственности с другими разделами теоретической физики.
Тогда закон кулона записывается так:
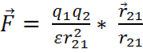 (1.1)
(1.1)
Формула 1.1 показывает, что может происходить как притяжение, если ![]() и
и ![]() разноименные заряды, так и отталкивание, если
разноименные заряды, так и отталкивание, если ![]() и
и ![]() — одноименные.
— одноименные.
Закон Кулона соответствует концепции дальнодействия, так как сила, действующая на ![]() , имеет причину — заряд
, имеет причину — заряд ![]() , находящийся от
, находящийся от ![]() на расстоянии
на расстоянии ![]() .
.
Наша "сверхзадача" — перейти к такой форме, которая связывала бы причину
и следствие в одной точке пространства. Для этого вводим понятие поля.
Сначала определим вектор напряженности поля заряда ![]() в точке 2, где
в точке 2, где
находится заряд ![]() :
:
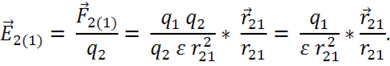
Эта формула не совсем удобна, так как ![]() имеет разное значение в разных средах (зависит от
имеет разное значение в разных средах (зависит от ![]() ). Введем вектор электрической индукции поля
). Введем вектор электрической индукции поля
заряда ![]() , равный:
, равный:
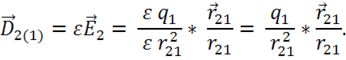
Проведем обобщение этой формулы:
1) сначала отвлечемся от точки 2 и напишем формулу для любой точки поля: 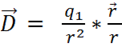 ,
,
2) затем напишем для любого заряда ![]() , создающего поле:
, создающего поле:
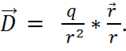 (1.2)
(1.2)
Формула (1.2) означает, что поле вектора ![]() обладает сферической
обладает сферической
симметрией. (Рис.4, а и б).
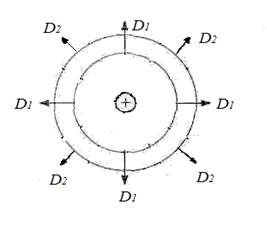 а)
а)
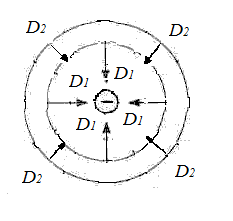
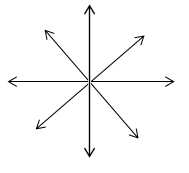
б) 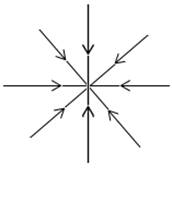
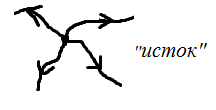
Рис 4. Силовые линии точечного заряда: а) положительный заряд, б) отрицательный заряд.
Это хорошо известные "школьные" картинки. Они показывают, что силовые линии могут выходить (" вытекать" ) из заряда — случай a), могут входить (" втекать") в заряд — случай б). Что является дифференциальной причиной такого "истока" и "стока" в данной точке поля, нам и предстоит выяснить. Но сначала докажем интегральную теорему для потока вектора электрической индукции, это и есть 2-я (электростатическая) теорема Остроградского-Гаусса.
II. 2-я (электростатическая) теорема Остроградского-Гаусса
Необходимо вычислить поток вектора электрической индукции через
произвольную замкнутую поверхность в случае произвольного распределения заряда, т. е. 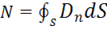 . Вычисление проведем в несколько этапов, постепенно обобщая результаты.
. Вычисление проведем в несколько этапов, постепенно обобщая результаты.
I. Сначала вычислим элементарный поток вектора электрической индукции 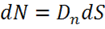 т. е. поток вектора
т. е. поток вектора ![]() через элементарную площадку
через элементарную площадку ![]() отстоящую от точечного заряда
отстоящую от точечного заряда ![]() на расстоянии
на расстоянии ![]() .
.
Для определенности пусть заряд ![]() — положительный. Тогда (см. рис. 5)
— положительный. Тогда (см. рис. 5)
Рис.5
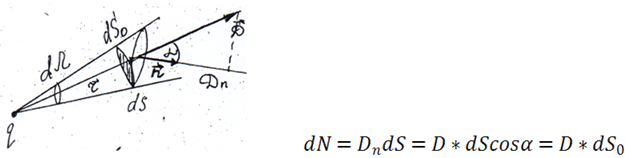
где ![]() — элементарная площадка, перпендикулярная радиусу-вектору
— элементарная площадка, перпендикулярная радиусу-вектору ![]() и равная
и равная 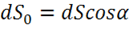 .
.
Подставляем вместо ![]() его значение для точечного заряда, т. е.
его значение для точечного заряда, т. е. ![]() и получаем, что поток равен
и получаем, что поток равен 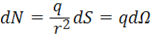 , где
, где ![]() — элемент телесного угла, под которым из точки, где расположен заряд
— элемент телесного угла, под которым из точки, где расположен заряд ![]() , видны поверхности
, видны поверхности ![]() и
и ![]() . При этом
. При этом ![]() равен
равен
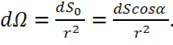 (1.3).
(1.3).
Обратите внимание на эту формулу. Она показывает, что ![]() может
может
иметь разные знаки, а именно:
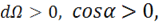 (1.4а)
(1.4а)
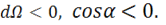 (1.4б)
(1.4б)
Учитывая (1.3) получаем для потока выражение:
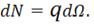 (1.5)
(1.5)
2. Вычислим поток вектора электрической индукции через произвольную
замкнутую поверхность от одного точечного заряда. Для этого используем только что доказанный результат. Рассмотрим два случая:
а) Заряд находится внутри замкнутой поверхности S. Тогда согласно рис. 6:
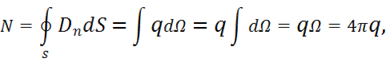
поскольку полный телесный угол, под которым изнутри видна замкнутая поверхность, равен 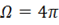 .
.
 рис 6.
рис 6.
Итак, в этом случае поток равен
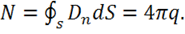 (1.6)
(1.6)
б) Заряд ![]() находится вне замкнутой поверхности S. Тогда поток
находится вне замкнутой поверхности S. Тогда поток
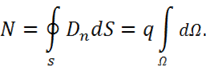
Рассмотрим два элемента поверхности ![]() и
и ![]() , которые из точки, где расположен заряд, видны под одним и тем же по величине телесным углом
, которые из точки, где расположен заряд, видны под одним и тем же по величине телесным углом ![]() (рис.7).
(рис.7).
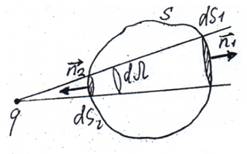 рис 7.
рис 7.
Однако площадка ![]() видна под положительным телесным углом
видна под положительным телесным углом ![]() , потому что нормаль
, потому что нормаль ![]() образует острый угол с радиусом-вектором. Площадка
образует острый угол с радиусом-вектором. Площадка ![]() видна под отрицательным телесным углом
видна под отрицательным телесным углом ![]() , так как нормаль
, так как нормаль ![]() образует тупой угол с радиусом-вектором. В сумме же эти два телесных угла компенсируют друг друга, т. е.
образует тупой угол с радиусом-вектором. В сумме же эти два телесных угла компенсируют друг друга, т. е. 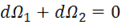 . В итоге
. В итоге 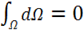 . Тогда поток будет равен
. Тогда поток будет равен
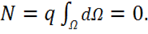 (1.7)
(1.7)
Рассматривая совместно (1.6) и (1.7), запишем:
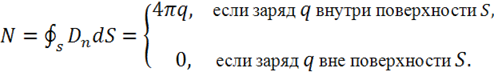 (1.8)
(1.8)
Итак, для одного точечного заряда теорема доказана.
3. Пусть имеется система точечных зарядов 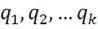 . Вычислим
. Вычислим
поток вектора электрической индукции через произвольную замкнутую, поверхность для системы точечных зарядов. Согласно принципу суперпозиции каждый заряд независимо от других создает свою ![]() и соответственно свой поток
и соответственно свой поток ![]() через поверхность
через поверхность![]() . Но учитывать надо только заряды, находящиеся внутри поверхности
. Но учитывать надо только заряды, находящиеся внутри поверхности ![]() согласно (1.8), так как заряды, находящиеся вне поверхности
согласно (1.8), так как заряды, находящиеся вне поверхности ![]() вклада в поток не дадут. Тогда каждый заряд, находящийся внутри поверхности
вклада в поток не дадут. Тогда каждый заряд, находящийся внутри поверхности ![]() дает поток:
дает поток:
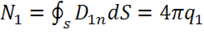 ,
, 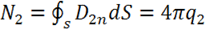 …,
…,
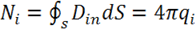 .
.
Просуммируем эти потоки:
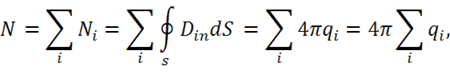
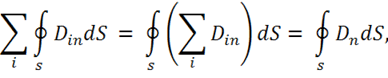
где 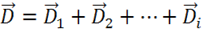 и
и 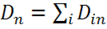 ,
, 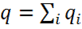 .
.
Тогда поток равен:
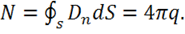 (1.9)
(1.9)
Формально получен такой же результат, что и в (1.6) , но он применим,
для более общего случая.
4. Рассмотрим непрерывное распределение заряда ![]() по объему V,
по объему V,
ограниченному поверхностью ![]() . Характеристикой такого распределения
. Характеристикой такого распределения
является объемная плотность электрического заряда ![]() , определяемая
, определяемая
следующим образом:
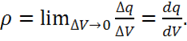 (1.10)
(1.10)
При этом элемент объема ![]() имеет заряд
имеет заряд 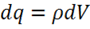 , заряд же всего
, заряд же всего
объема вычисляется 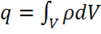 , где
, где ![]() в общем случае может зависеть как от координат, так и от времени, т. е.
в общем случае может зависеть как от координат, так и от времени, т. е. 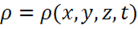 .
.
Разбиваем мысленно объем V на элементарные объемы ![]() такие, что заряд
такие, что заряд ![]() объема
объема ![]() можно было бы считать точечным. Тогда этот заряд равен
можно было бы считать точечным. Тогда этот заряд равен 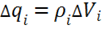 . Согласно доказанной ранее теореме каждый такой точечный заряд создает свой поток, равный:
. Согласно доказанной ранее теореме каждый такой точечный заряд создает свой поток, равный:
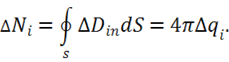
Здесь ![]() — вектор электрической индукции, создаваемой зарядом
— вектор электрической индукции, создаваемой зарядом ![]() . Для этих зарядов так же выполняется принцип суперпозиции. Просуммируем все потоки от зарядов
. Для этих зарядов так же выполняется принцип суперпозиции. Просуммируем все потоки от зарядов ![]() и перейдем к пределу суммы:
и перейдем к пределу суммы:
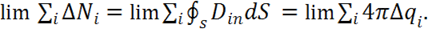 (1.11)
(1.11)
Рассмотрим по отдельности каждое выражение, вспоминая, что предел
такой суммы — соответствующий интеграл:
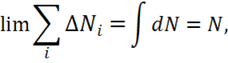
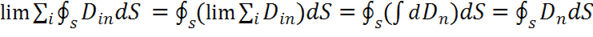 ,
,
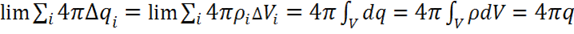 . (1.12)
. (1.12)
Тогда вместо (1.11) на основании равенств (1.12) получаем, что
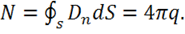 (1.13)
(1.13)
Итак, в случае произвольного распределения заряда (см. (1.9), (1.13)) поток вектора электрической индукции через произвольную замкнутую поверхность ![]() равен
равен ![]() , где
, где ![]() — заряд, находящийся внутри поверхности
— заряд, находящийся внутри поверхности ![]() . Если внутри данной поверхности
. Если внутри данной поверхности ![]() нет зарядов, то поток равен нулю. Это и есть 2-я теорема Остроградского-Гаусса. Она позволяет достаточно просто вычислять значение вектора
нет зарядов, то поток равен нулю. Это и есть 2-я теорема Остроградского-Гаусса. Она позволяет достаточно просто вычислять значение вектора ![]() для ряда случаев, т. е. решать конкретные задачи.
для ряда случаев, т. е. решать конкретные задачи.
III. Переходим к нахождению 4-го уравнения Максвелла. Для этого рассмотрим совместно две интегральные теоремы — I-ю и 2-ю теоремы Остроградского-Гаусса. По 1-й теореме (из векторного анализа) запишем для потока любого вектора ![]() :
:
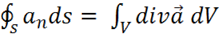 .
.
Для потока вектора ![]() получаем, полагая
получаем, полагая 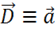 :
:
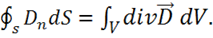 (1.14)
(1.14)
По 2-й теореме для потока вектора ![]()
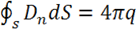 .
.
Будем считать, что заряд ![]() распределен по объему с плотностью
распределен по объему с плотностью ![]() .
.
Тогда для потока вектора ![]() можно записать:
можно записать:
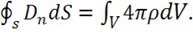 (1.15)
(1.15)
В левой части (1.14) и (1.15) поток вектора ![]() , следовательно, можно
, следовательно, можно
приравнять и правые части:
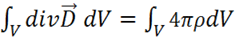 .
.
Для элемента объема ![]() получаем:
получаем:
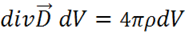 ,
, 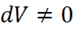 ,
,
откуда следует, что
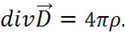 (1.16)
(1.16)
Это и есть искомое четвертое уравнение Максвелла.
Выясним его физический смысл. В теоретической физике уравнения записываются следующим образом: в правой части – причина, в левой – следствие. Согласно (1.16) в левой части стоит 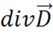 . Как известно из векторного анализа дивергенция характеризует источник поля данного вектора. Нас интересует, что является причиной образования источника поля
. Как известно из векторного анализа дивергенция характеризует источник поля данного вектора. Нас интересует, что является причиной образования источника поля ![]() в данной точке. Ответ в правой части уравнения (1.16) — причиной является объемная плотность заряда
в данной точке. Ответ в правой части уравнения (1.16) — причиной является объемная плотность заряда ![]() в этой же самой точке поля.
в этой же самой точке поля.
Итак, причиной источника поля ![]() является объемная плотность заряда
является объемная плотность заряда ![]() в этой же самой точке. При этом возможны три случая:
в этой же самой точке. При этом возможны три случая:
1) если 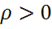 (положительные заряды), то
(положительные заряды), то 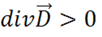 — это означает, что в данной точке "исток"
— это означает, что в данной точке "исток" ![]() ("начало" силовых линий
("начало" силовых линий![]() );
);
2) если 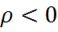 (отрицательные заряды ), то
(отрицательные заряды ), то 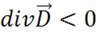 — это означает "сток" (конец силовых линий
— это означает "сток" (конец силовых линий ![]() );
);

3) если 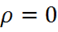 , то
, то 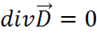 , но
, но 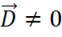 — это означает, что линии
— это означает, что линии ![]() идут непрерывно:
идут непрерывно:
![]()
4-е уравнение Максвелла является обобщением закона Кулона.
1 закон Кулона соответствует концепции дальнодействия, как это уже
отмечалось, потому что причина – заряд ![]() и следствие — сила, действующая на заряд
и следствие — сила, действующая на заряд ![]() , находятся в разных точках пространства.
, находятся в разных точках пространства.
4-е уравнение Максвелла соответствует концепции близкодействия, так как
причина — объемная плотность заряда ![]() и следствие —
и следствие — 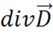 связаны
связаны
в одной и той же точке. Таким образом, 4-е уравнение Максвелла описывает любую точку поля, даже такую, в которой отсутствует заряд (см. случай 3).
2 закон Кулона — закон взаимодействия точечных зарядов. 4-е уравнение
Максвелла применимо для любого распределения зарядов и даже тогда, когда 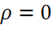 .
.
3 закон Кулона — это закон электростатики. Так взаимодействуют неподвижные заряды.
4-е уравнение Максвелла — уравнение электродинамики. Оно применимо и в
случае 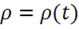 .
.
§2. 3-е уравнение Максвелла как обобщение экспериментального факта
отсутствия свободных магнитных зарядов в природе.
Кулон экспериментально установил закон взаимодействия магнитных полюсов, предполагая, что в каждом полюсе содержатся свободные магнитные
заряды:
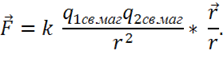
По аналогии с электростатикой вводились векторы ![]() и
и ![]() :
:
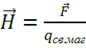 ,
, 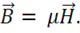
Затем можно было записать 2-ю теорему Остроградского-Гаусса для
вектора магнитной индукции:
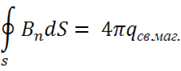
Но на этом аналогия с электростатикой заканчивается, так как в природе
до сих пор не обнаружены частицы, имеющие свободный магнитный заряд.
Природа не устроена по шаблону, который пытается навязать ей человек.
Природа гораздо богаче!
Итак, в соответствии с экспериментальным фактом отсутствия свободных магнитных зарядов в природе полагаем, что 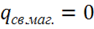 , следовательно всегда:
, следовательно всегда:
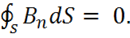 (1.17)
(1.17)
Применяя 1-ю теорему Остроградского-Гаусса для вектора ![]() , получаем:
, получаем:
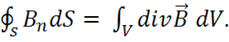 (1.18)
(1.18)
Рассматривая совместно (1.17) и (1.18), записываем 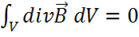 . Откуда для элемента
. Откуда для элемента ![]() имеем
имеем 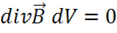 , но
, но 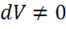 , тогда получаем окончательно:
, тогда получаем окончательно:
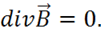 (1.19)
(1.19)
Это и есть искомое третье уравнение Максвелла.
Физический смысл уравнения: магнитное поле — поле вектора магнитной
индукции ![]() не имеет источников, так как в природе отсутствуют носители свободных магнитных зарядов. Следовательно, силовые линии
не имеет источников, так как в природе отсутствуют носители свободных магнитных зарядов. Следовательно, силовые линии ![]() всегда
всегда
замкнуты, идут непрерывно.
3-е уравнение Максвелла соответствует концепции близкодействия, так как имеет дифференциальную форму.
Отметим, что еще в 1932 году Дирак создал квантовую теорию, из
которой следовало существование частиц, несущих свободный магнитный заряд, т. е. монополей. Но до сих пор монополи Дирака в природе не обнаружены, по крайней мере, в исследованной области Вселенной.
§3. 2-e уравнение Максвелла как обобщение закона электромагнитной индукции
Явление электромагнитной индукции было открыто Фарадеем в 1832 году.
Оно заключается в следующем: при любом изменении магнитного потока, пронизывающего произвольную поверхность ![]() , опирающуюся на замкнутый проводящий контур
, опирающуюся на замкнутый проводящий контур  , в контуре возникает индукционный ток. (Рис. 8)
, в контуре возникает индукционный ток. (Рис. 8)
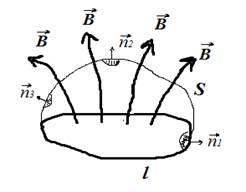
Рис. 8. Поток вектора ![]() через поверхность
через поверхность ![]() .
.
Закон электромагнитной индукции с учетом правила Ленца имеет вид:
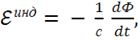 (1.20)
(1.20)
где ![]() — эдс индукции,
— эдс индукции, ![]() — магнитный поток,
— магнитный поток, ![]() — электродинамическая
— электродинамическая
постоянная в гауссовой системе.
При этом эдс индукции возникает (наводится) в контуре  , а магнитный поток меняется через поверхность
, а магнитный поток меняется через поверхность![]() , и необязательно через всю поверхность. Может, как показывают многочисленные эксперименты, даже через некоторые участки поверхности. Впечатляющие опыты, в которых участвуют простые школьные приборы (демонстрационный гальванометр, катушка индуктивности и постоянный магнит) сейчас доступны для наблюдения явления на уроках в школе.
, и необязательно через всю поверхность. Может, как показывают многочисленные эксперименты, даже через некоторые участки поверхности. Впечатляющие опыты, в которых участвуют простые школьные приборы (демонстрационный гальванометр, катушка индуктивности и постоянный магнит) сейчас доступны для наблюдения явления на уроках в школе.
Закон (1.20) имеет интегральную форму, что мы сейчас и покажем, а
уж затем перейдем к дифференциальной форме.
Рассмотрим левую часть (1.20). По определению эдс — это работа, совершаемая по перемещению единичного положительного заряда вдоль замкнутого контура  под действием некоторой электрическое напряженности, в данном случае наведенной, т. е. индуцированной напряженности
под действием некоторой электрическое напряженности, в данном случае наведенной, т. е. индуцированной напряженности ![]() . Тогда можно записать:
. Тогда можно записать:
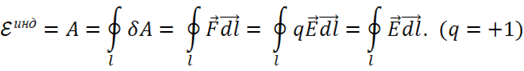
Итак, получили, что:
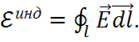 (1.21)
(1.21)
Теперь переходим к правой части (1.20). Используем определение магнитного потока:
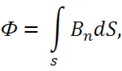
находим
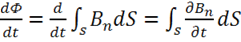 .
.
При этом, считая поверхность фиксированной, предполагаем, что изменение магнитного потока происходит за счет изменения магнитной индукции ![]() . Тогда производную
. Тогда производную ![]() можно внести под знак интеграла. Итак, получаем:
можно внести под знак интеграла. Итак, получаем:
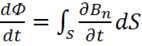 (1.22)
(1.22)
Подставляем найденные выражения в (1.20)
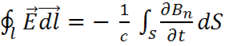 (1.23)
(1.23)
Используем теорему Стокса:
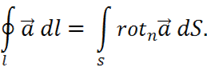
Применяем теорему Стокса, полагая 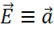 , Тогда:
, Тогда:
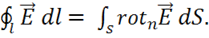 (1.24)
(1.24)
Рассматривая совместно (1.23) и (1.24), получаем:
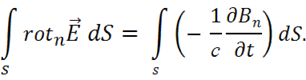
Для элемента поверхности ![]() выполняется равенство:
выполняется равенство:
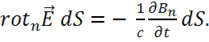
Но так как 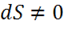 , то
, то
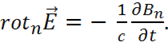 (1.25)
(1.25)
Мы получили пока соотношение для проекции на нормаль некоторых векторов. Но поскольку элемент поверхности выбран произвольно, нормаль ![]() ориентировано в пространстве соответственно произвольно (см. рис.8), то из равенства нормальных составляющих векторов следует равенство векторов:
ориентировано в пространстве соответственно произвольно (см. рис.8), то из равенства нормальных составляющих векторов следует равенство векторов:
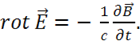 (1.26)
(1.26)
Это и есть искомое 2-е уравнение Максвелла.
Физический смысл 2-го уравнения Максвелла: вихрь электрической напряженности в некоторой точке создается изменением вектора магнитной индукции в той же самой точке. Иначе говоря, переменным магнитным полем порождается вихревое электрическое поле. Вихревое поле имеет замкнутые силовые линии. Если в какой-то точке 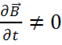 и направлено вверх (см. рис 9), то
и направлено вверх (см. рис 9), то ![]() направлен вниз. В окрестности этой точки происходит циркуляция вектора
направлен вниз. В окрестности этой точки происходит циркуляция вектора ![]() в плоскости, перпендикулярной
в плоскости, перпендикулярной ![]() .
.
Рис 9. Связь ![]() и
и ![]() .
.
2-е уравнение Максвелла показывает, что Фарадей открыл новое по качеству электрическое поле — вихревое, и новый способ создания электрического
поля — с помощью переменного магнитного поля!
Но как будет показано в главе II, электрическое поле может быть и безвихревым, т. е. 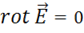 . Силовые линии такого поля незамкнуты, связаны с электрическими зарядами.
. Силовые линии такого поля незамкнуты, связаны с электрическими зарядами.
2-е уравнение Максвелла является обобщением закона электромагнитной индукции:
1) Закон электромагнитной индукции соответствует концепции дальнодействия. В самом деле, как, мы уже отмечали, изменение магнитного поля может происходить в какой-то одной части поверхности S, а
индукционный ток возникает вдоль контура 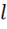 . Это означает, что причина
. Это означает, что причина
— изменение магнитного потока и следствие — ток в контуре разделены в
пространстве.
2-е уравнение Максвелла соответствует концепции близкодействия, так
как причина — скорость изменения вектора ![]() и следствие — вихрь электрической напряженности связаны в одной и той же точке поля. При этом, как мы покажем в следующих пунктах, 2-е уравнение Максвелла описывает любую точку поля.
и следствие — вихрь электрической напряженности связаны в одной и той же точке поля. При этом, как мы покажем в следующих пунктах, 2-е уравнение Максвелла описывает любую точку поля.
2) Максвелл раскрыл сущность явления электромагнитной индукции — возникновение вихревого электрического поля при изменении магнитного поля,
это означает, что явление электромагнитной индукции есть объективное
свойство электромагнитного поля.
3) Проводящий контур играет второстепенную роль — роль индикатора, позволяющего обнаружить явление. Но само явление может происходить и без
контура. Например, в нашей аудитории, так как везде есть свет, а это электромагнитные волны, в которых связаны переменные во времени и вихревые электрическое и магнитное поля (см. Глава V).
4) Роль вещества, отметим снова, второстепенная. Запишем уравнение для вакуума. В вакууме 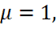 тогда
тогда 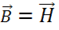 и уравнение имеет вид:
и уравнение имеет вид:
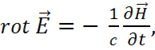 (1.27)
(1.27)
но в среде 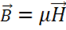 , тогда уравнение примет вид:
, тогда уравнение примет вид:
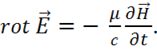 (1.28)
(1.28)
Для ферромагнетиков 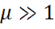 , следовательно ферромагнитные материалы усиливают явление. Это широко применяется в технике.
, следовательно ферромагнитные материалы усиливают явление. Это широко применяется в технике.
Вообще значение открытия Фарадеем явления электромагнитной индукции и выяснения Максвеллом сущности явления для современное цивилизации огромно и его трудно переоценить!
§4. 1-е уравнение Максвелла как обобщение закона Био-Савара-Лапласа.
Уравнение непрерывности. Ток смешения.
План
I. 1-е уравнение Максвелла, как обобщение закона Био-Савара-Лапласа для постоянного тока.
II. Уравнение непрерывности — дифференциальная форма закона сохранения электрического заряда.
III. Гипотеза Максвелла о токе смещения. 1-е уравнение Максвелла для переменного тока.
I. Согласно закону Био-Савара-Лапласа магнитная напряженность бесконечного прямого проводника, по которому течет постоянный ток, равна:
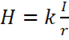 ,
,
где 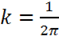 — в СИ,
— в СИ, 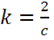 — в гауссовой системе.
— в гауссовой системе.
На рис. 10 изображены силовые линии и вектор ![]() в некоторых точках.
в некоторых точках.
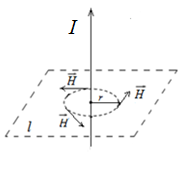 Рис. 10. Циркуляция
Рис. 10. Циркуляция ![]() вдоль силовых линий.
вдоль силовых линий.
Видно, что вектор ![]() циркулирует вдоль силовых линий. Запишем значение
циркулирует вдоль силовых линий. Запишем значение ![]() в гауссовой системе единиц:
в гауссовой системе единиц:
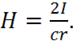 (1.29)
(1.29)
Формула (1.29) показывает, что причина — сила тока 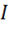 и следствие — магнитная напряженность
и следствие — магнитная напряженность ![]() разделены расстоянием
разделены расстоянием ![]() (радиус силовой линии), что соответствует концепции дальнодействия. Необходимо написать такое уравнение, в котором причина и следствие находились бы в одной точке.
(радиус силовой линии), что соответствует концепции дальнодействия. Необходимо написать такое уравнение, в котором причина и следствие находились бы в одной точке.
Но сначала перейдем к интегральной форме. Для этого умножим (1.29) слева и справа на ![]() — длину окружности, т. е. длину силовой линии радиуса
— длину окружности, т. е. длину силовой линии радиуса ![]() . Тогда получим:
. Тогда получим:
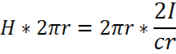
или
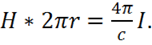 (1.30)
(1.30)
Покажем, что левая и правая части теперь имеют интегральную форму. Вычислим циркуляцию ![]() вдоль силовой линии радиуса
вдоль силовой линии радиуса ![]() , т. е.
, т. е. 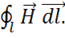
Выберем ![]() , совпадающим по направлению с
, совпадающим по направлению с ![]() , затем используем постоянство
, затем используем постоянство ![]() по величине на данной силовой линии и получаем:
по величине на данной силовой линии и получаем:
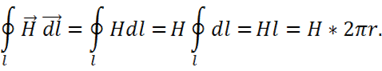
Итак,
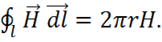 (1.31)
(1.31)
Теперь нам надо показать, что 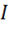 тоже есть некоторый интеграл. Для этого
тоже есть некоторый интеграл. Для этого
введем известное из курса общей физики понятие вектора плотности тока проводимости  .
.
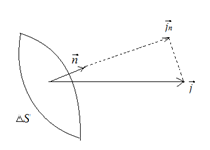 Рис. 11. Вектор
Рис. 11. Вектор ![]()
Для случая произвольно ориентированной площадки ![]() проводника, через которую протекает ток
проводника, через которую протекает ток ![]() , получаем:
, получаем:

Тогда
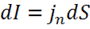
и сила тока равна:
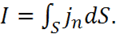 (1.32)
(1.32)
Подставляем полученные интегральные выражения (1.31) и (1.32) вместо (1.30) и получаем:
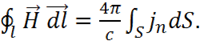 (1.33)
(1.33)
Используем теорему Стокса для ![]() :
:
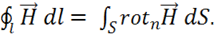 (1.34)
(1.34)
Совместное рассмотрение (1.33) и (1.34) позволяет записать:
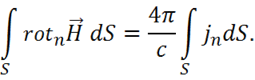
Для элемента поверхности ![]() , следовательно, выполняете равенство:
, следовательно, выполняете равенство:
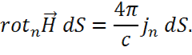
Поскольку 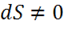 , то можно написать:
, то можно написать:
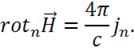
Но элемент поверхности ![]() выбран произвольно, поэтому равенство выполняется и для векторов:
выбран произвольно, поэтому равенство выполняется и для векторов:
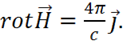 (1.35)
(1.35)
Это искомое 1-е уравнение Максвелла для постоянного тока. Возникает вопрос, применимо ли оно и для описания поля переменного тока?
Чтобы ответить на этот вопрос, необходимо ввести некоторый критерий, конечно, в дифференциальной форме, позволяющий отделять случай постоянного тока от случая переменного тока. Для этого сделаем отступление и рассмотрим закон сохранения электрического заряда.
II. Пусть в некотором объеме V находится заряд ![]() . За счет чего может происходить изменение заряда
. За счет чего может происходить изменение заряда ![]() ? Только за счет втекания или вытекания зарядов через поверхность
? Только за счет втекания или вытекания зарядов через поверхность ![]() , ограничивающую объем V (см. Рис.12), т. е. за счет силы тока
, ограничивающую объем V (см. Рис.12), т. е. за счет силы тока 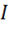 или иначе, потока вектора плотности тока
или иначе, потока вектора плотности тока 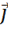 через
через ![]() .
.
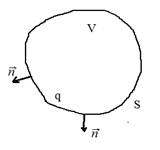 Рис. 12. Заряд в объеме V.
Рис. 12. Заряд в объеме V.
Других способов изменения заряда нет в природе. Это фундаментальный закон природы.
Закон можно записать в интегральной форме:
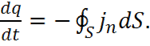 (1.36)
(1.36)
Рассмотрим три разных случая:
1) Пусть 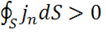 — это означает, что заряды вытекают из объема V. Согласно (1.36)
— это означает, что заряды вытекают из объема V. Согласно (1.36) 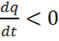 , т. е. заряд
, т. е. заряд ![]() убывает, что логично.
убывает, что логично.
2) Если 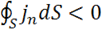 , т. е. заряды втекают в объем V через поверхность
, т. е. заряды втекают в объем V через поверхность ![]() , то согласно (1.36)
, то согласно (1.36) 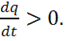 Это значит, что заряд увеличивается.
Это значит, что заряд увеличивается.
3) Если 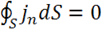 , то и
, то и 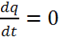 — заряд сохранится. Значит в исходном уравнении (1.36) знаки выбраны правильно.
— заряд сохранится. Значит в исходном уравнении (1.36) знаки выбраны правильно.
Теперь переходим к дифференциальной форме закона. Пусть заряд ![]() распределен по объему с плотностью
распределен по объему с плотностью ![]() . Тогда заряд представим так:
. Тогда заряд представим так:
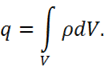
Находим
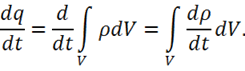
При этом сделано предположение, что объем не меняется, а все изменение заряда происходит за счет изменения объемной плотности. С учетом полученного выражения вместо (1.36) запишем:
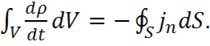 (1.37)
(1.37)
Применим 1-ю теорему Остроградского-Гаусса к вектору 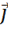 :
:
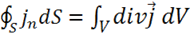 (1.38)
(1.38)
и подставим правую часть (l.38) в (1.37):
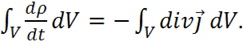 (1.39)
(1.39)
Для элемента объема ![]() справедливо равенство:
справедливо равенство:
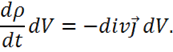
Так как 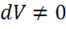 , то получаем:
, то получаем:
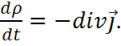 (1.40)
(1.40)
Это и есть искомое дифференциальное уравнение, которое называется уравнением непрерывности.
Рассмотрим возможные частные случаи.
1) Если 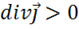 , то
, то 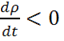 – т. е. плотность заряда
– т. е. плотность заряда ![]() в данной точке убывает, если ток вытекает.
в данной точке убывает, если ток вытекает.
2) Если 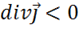 , то
, то 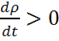 — т. е. плотность заряда в данной точке увеличивается, если ток втекает.
— т. е. плотность заряда в данной точке увеличивается, если ток втекает.
3) Если 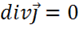 при
при ![]() , то
, то 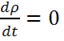 и
и 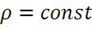 – ток течет, но плотность заряда
– ток течет, но плотность заряда ![]() не меняется.
не меняется.
Случаи 1 и 2 — это случаи переменного тока. При этом
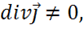 (1.41)
(1.41)
Случай 3 — случай постоянного тока. При этом
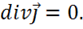 (1.42)
(1.42)
Итак, получены критерии, позволяющие отделить случай переменного тока
от постоянного тока, это условия (1.41) и (1.42).
III. Проверим, удовлетворяет ли уравнение (1.35) требованиям уравнениянепрерывности. Для этого образуем дивергенцию от уравнения (1.35):
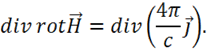
Согласно тождеству векторного анализа 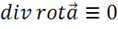 получаем, что
получаем, что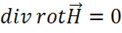 и, следовательно,
и, следовательно, 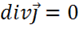 .
.
Это означает, что уравнение (1.35) удовлетворяет уравнению непрерывности только для постоянного тока. Для переменного тока, как мы получили ранее, 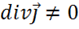 , но уравнение (1.35) этого не дает. Возникает противоречие между фундаментальным законом (уравнение непрерывности) и частным уравнением (1.35) .
, но уравнение (1.35) этого не дает. Возникает противоречие между фундаментальным законом (уравнение непрерывности) и частным уравнением (1.35) .
Максвелл разрешил это противоречие следующим образом. Он предположил, что в случае переменного тока в уравнение (1.35) надо к вектору ![]() добавить еще некоторый вектор, который он назвал вектором плотности тока смещения, т. е.
добавить еще некоторый вектор, который он назвал вектором плотности тока смещения, т. е. ![]() . Иначе, вместо (1.35) надо записать:
. Иначе, вместо (1.35) надо записать:
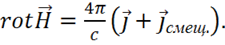 (1.43)
(1.43)
Выясним, как этот дополнительный вектор устраняет противоречие, т. е. согласует уравнение (1.43) с требованиями уравнения непрерывности (1.41)
и (1.42).
Для этого снова образуем дивергенцию от обеих частей уравнения (1.43):
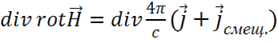 .
.
Но 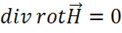 , следовательно
, следовательно 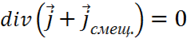 ,
, 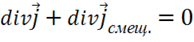 . Иначе:
. Иначе:
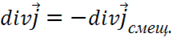 (1.44)
(1.44)
Теперь имеются две возможности
1) Если  , то
, то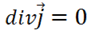 — удовлетворяется случай постоянного тока.
— удовлетворяется случай постоянного тока.
2) Если 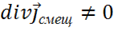 , то
, то 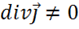 — удовлетворяется случай переменного тока.
— удовлетворяется случай переменного тока.
Это означает, что противоречие с уравнением непрерывности устраняется. Остается найти явный вид ![]() . Для этого используем уравнение непрерывности (1.40) и соотношение (1.44). Тогда получаем:
. Для этого используем уравнение непрерывности (1.40) и соотношение (1.44). Тогда получаем:
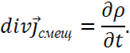
Выразим ![]() из 4-го уравнения Максвелла:
из 4-го уравнения Максвелла: 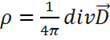 и подставим в предыдущую формулу:
и подставим в предыдущую формулу:
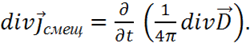 (1. 45)
(1. 45)
Докажем следующее важное свойство для любого вектора ![]() :
:
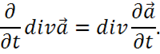
В самом деле, 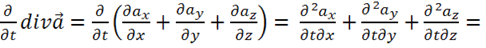
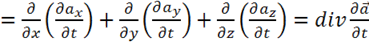 .
.
Это означает, что операторы ![]() и
и ![]() коммутируют, т. е. их можно переставлять. Аналогично доказывается, что
коммутируют, т. е. их можно переставлять. Аналогично доказывается, что
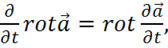 (1.46)
(1.46)
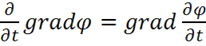 (1.47)
(1.47)
Используя (1.46) для вектора ![]() , можно (1.45) переписать так:
, можно (1.45) переписать так:
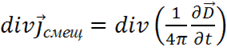 .
.
Максвелл предположил, что искомый вектор ![]() равен:
равен:
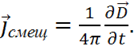 (1.49)
(1.49)
Подставив (1.49) в уравнение (1.43), получаем:
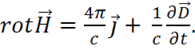 (1.50)
(1.50)
Это и есть искомое 1-е уравнение Максвелла.
Физический смысл уравнения (1.50): в природе существуют две причины возбуждения вихря магнитной напряженности — это плотность тока проводимости 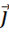 и плотность тока смещения
и плотность тока смещения ![]() . Ток проводимости обусловлен движением свободных заряженных частиц, а ток смещения есть скорость изменения вектора электрической индукции
. Ток проводимости обусловлен движением свободных заряженных частиц, а ток смещения есть скорость изменения вектора электрической индукции ![]() в данной точке поля. Иначе — магнитное вихревое поле в данной точке создается плотностью тока проводимости и скоростью изменения вектора электрической индукции. Магнитное поле вихревое, имеет замкнутые силовые линии.
в данной точке поля. Иначе — магнитное вихревое поле в данной точке создается плотностью тока проводимости и скоростью изменения вектора электрической индукции. Магнитное поле вихревое, имеет замкнутые силовые линии.
1-е уравнение Максвелла есть обобщение закона Био-Савара-Лапласа.
1) Закон Био-Савара-Лапласа соответствует концепции дальнодействия,
так как причина — сила тока 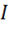 и следствие — магнитная напряженность
и следствие — магнитная напряженность ![]()
находятся в разных точках.
1-е уравнение Максвелла соответствует концепции близкодействия,
так как две причины — плотность тока проводимости 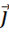 и скорость изменения
и скорость изменения
вектора электрической индукции ![]() находятся в той же самой точке поля,
находятся в той же самой точке поля,
что и вихрь магнитной напряженности — 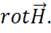
2) Закон Био-Савара-Лапласа — закон постоянного тока.
1-е уравнение Максвелла обобщено и на случай переменного тока.
3) В вакууме, где нет проводящего тока вещества, закон Био-Савара-Лапласа
при ![]() никакую
никакую ![]() дать не может.
дать не может.
1-е уравнение Максвелла в вакууме (при  ,
, 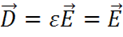 ) имеет вид:
) имеет вид:
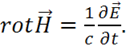 (1.51)
(1.51)
Уравнение (1.51) показывает, что вихревое магнитное поле создается переменным электрическим полем. Это свойство самого электромагнитного поля,
как и явление электромагнитной индукции. Отсюда — исключительное значение
гипотезы Максвелла о токе смещения. Отметим лишь в общих чертах некоторые моменты.
1. С введением плотности тока смещения в виде (1.49) в уравнениях электродинамики появляется симметрия, отражающая симметрию свойств поля, что особенно хорошо видно на уравнениях для вакуума:
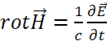 — теоретическое предсказание Максвелла,
— теоретическое предсказание Максвелла,
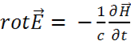 — открытое Фарадеем явление электромагнитной индукции и его обобщение Максвеллом.
— открытое Фарадеем явление электромагнитной индукции и его обобщение Максвеллом.
2. Гипотеза о токе смешения "примирила" систему уравнений Максвелла
с основными законами сохранения в электродинамике: с законом сохранения
электрического заряда, с законом сохранения и превращения энергии электромагнитного поля, с законом сохранения импульса поля и вещества.
3. Гипотеза о токе смещения привела к тому, что, как выяснилось в начале
XX века, система уравнений Максвелла полностью соответствует требованиям
специальной теории относительности (см. Глава VIII).
4. Гипотеза о токе смещения оказалась очень плодотворной. Например, она
позволила Максвеллу предсказать теоретически существование электромагнитных волн в природе.
Необходимо отметить, что плотность тока проводимости 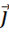 и плотность
и плотность
тока смешения 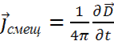 имеют различную природу, но вызывают одинаковое магнитное действие — вихрь магнитной напряженности —
имеют различную природу, но вызывают одинаковое магнитное действие — вихрь магнитной напряженности — ![]()
§ 5. Система уравнений Максвелла
Запишем систему уравнений Максвелла для среды, причем в левом столбце в СИ, в правом — в гауссовой системе единиц:
|
СИ |
Гаусс |
|
|
|
|
Три уравнения связи |
|
|
|
|
Запись уравнений в разных системах единиц, как это и должно быть, не
изменяет их физического смысла. Последние три уравнения (для 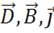 ) называются уравнениями связи и имеют некоторые ограничения, которые мы рассмотрим подробно в Главе V I.
) называются уравнениями связи и имеют некоторые ограничения, которые мы рассмотрим подробно в Главе V I.
Отметим формальные свойства уравнений:
1) Система уравнений Максвелла — это система дифференциальных уравнений первого порядка в частных производных, что соответствует концепции
близкодействия.
2) Уравнения Максвелла – линейные, что соответствует принципу суперпозиции.
3) Уравнения Максвелла симметричны, что отражает свойства поля, и асимметричны, что отражает свойства вещества.
4) Уравнений Максвелла в данной форме четыре. Как известно из векторного
анализа, для характеристики поля вектора ![]() необходимо знать
необходимо знать ![]() и
и![]() . Но поскольку поле — электромагнитное, то в уравнении поля должно быть две дивергенции (
. Но поскольку поле — электромагнитное, то в уравнении поля должно быть две дивергенции (![]() и
и ![]() ) и два ротоpa (
) и два ротоpa (![]() и
и ![]() ). Для описания поля к системе уравнений Максвелла необходимо добавить три основных закона сохранения (см.§ 4) и граничные условия.
). Для описания поля к системе уравнений Максвелла необходимо добавить три основных закона сохранения (см.§ 4) и граничные условия.
§ 6. Закон сохранения и превращения энергии электромагнитного поля. Теорема Умова-Пойнтинга.
В 1874 г. русский физик Умов защитил докторскую диссертацию на тему:
«Уравнения движения энергии в телах». В 1884 г. английский физик Пойнтинг опубликовал работу «О переносе энергии в электромагнитном поле».
В дифференциальной форме уравнение Умова имеет вид:
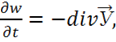 — сравните с уравнением непрерывности!
— сравните с уравнением непрерывности!
Где ![]() — объемная плотность данного вида энергии,
— объемная плотность данного вида энергии, ![]() — вектор Умова — вектор плотности потока этой энергии.
— вектор Умова — вектор плотности потока этой энергии.
В интегральной форме теорема Умова может быть записана в вид:
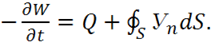 (1.52)
(1.52)
Уравнение (1.52) означает, что изменение данного вида энергии ![]() в объеме V может происходить за счет превращения в другой вид энергии с выделением
в объеме V может происходить за счет превращения в другой вид энергии с выделением
тепла ![]() и за счет втекания или вытекания, т. е. потока данного вида
и за счет втекания или вытекания, т. е. потока данного вида
энергии через поверхность ![]() . Знаки выбраны так же, как и в (1.36)
. Знаки выбраны так же, как и в (1.36)
(см. § 4 ), чтобы правильно описывать физический процесс.
Докажем теорему Умова для электромагнитного поля и выясним вид ![]() и
и ![]() для поля. Для этого сначала запишем согласно теореме Умова количество тепла, выделившегося в объеме V:
для поля. Для этого сначала запишем согласно теореме Умова количество тепла, выделившегося в объеме V:
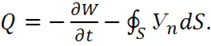 (1.53)
(1.53)
Перейдем теперь к доказательству теоремы для электромагнитного поля. Пусть в объеме V, содержащем поле и вещество, под действием поля выделилось некоторое количество тепла ![]() в единицу времени:
в единицу времени:
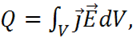 (1.54)
(1.54)
где 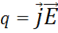 — дифференциальная форма закона Джоуля-Ленца, известная из курса общей физики.
— дифференциальная форма закона Джоуля-Ленца, известная из курса общей физики.
Наша "сверхзадача" — преобразовать (1.54) так, чтобы можно было сравнить с (1.53).
Рассмотрим по этапам эти преобразования
1) Выразим 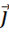 из 1-го уравнения Максвелла:
из 1-го уравнения Максвелла:
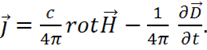 (1.55)
(1.55)
2) Подставим (1.55) в (1.54), сразу разбивая на два интеграла:
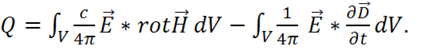 (1.56)
(1.56)
3) Используем тождество векторного анализа: 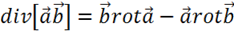
Пусть 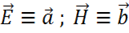 , тогда:
, тогда:
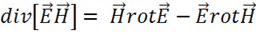 .
.
Отсюда
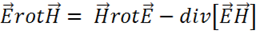 .
.
Заменим ![]() из 2-го уравнения Максвелла на
из 2-го уравнения Максвелла на 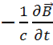 и получим
и получим
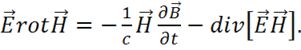 (1.57)
(1.57)
Это, как видно, преобразование для подинтегрального выражения в первом интеграле (1.56).
4) Подставим (1.57) в (1.56), сразу объединяя похожие члены с ![]() и
и ![]() в один интеграл:
в один интеграл:
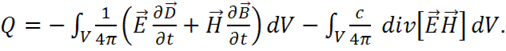 (1.58)
(1.58)
5) В первом интеграле (1.58):
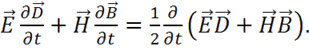 (1.59)
(1.59)
Докажем это. Рассмотрим правую часть и покажем, что получится левая:
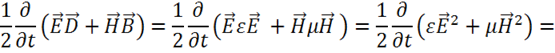
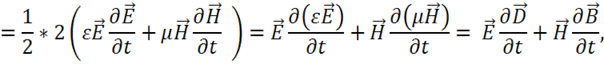
где использованы 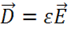 ,
, 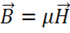 , что и требовалось доказать.
, что и требовалось доказать.
6) Подставим (1.59) в первый интеграл (1.58) и получим:
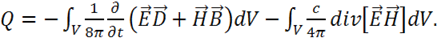 (1.60)
(1.60)
7) Преобразуем снова первый интеграл. Считая объем V фиксированным, выносим ![]() из-под знака интеграла:
из-под знака интеграла:
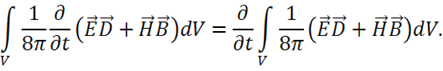
8) Преобразуем второй интеграл, используя 1-ю теорему Остроградского-Гаусса:
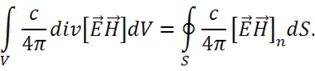
9) Подставим эти преобразованные интегралы в (1.60) и получим окончательно
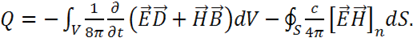 (1.61)
(1.61)
Сравниваем (1.61) с (1.53) и даем интерпретацию ![]() и
и ![]() для электромагнитного поля согласно (1.61):
для электромагнитного поля согласно (1.61):
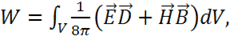 (1.62)
(1.62)
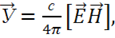 (1.63)
(1.63)
где формула (1.62) — формула для энергии электромагнитного поля,
(1.63) — формула для вектора плотности потока электромагнитной энергии, называемая вектором Умова-Пойнтинга.
Подведем итоги:
1. Доказана теорема Умова-Пойнтинга, т. е. выполнение закона сохранения
и превращения энергии для электромагнитного поля.
2. Получены в явном виде формулы для энергии и вектора плотности потока
энергии электромагнитного поля.
Обсудим подробнее эти формулы.
1) Энергия электромагнитного поля:
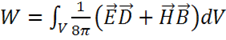 .
.
Эта формула означает, что энергия поля распределена (иногда говорят
"размазана") по всему объему, занятому полем, с объемной плотностью:
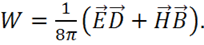 (1.64)
(1.64)
Объемная плотность электромагнитной энергии 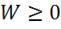 , но всегда энергия
, но всегда энергия
всего поля 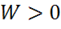 — положительна. При этом энергия поля и плотность энергии разделяется на электрическую
— положительна. При этом энергия поля и плотность энергии разделяется на электрическую 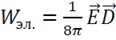 и магнитную
и магнитную 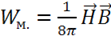 . Энергия не аддитивна, так как есть еще энергия взаимодействия.
. Энергия не аддитивна, так как есть еще энергия взаимодействия.
Например, для двух полей плотность энергии
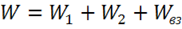 .
.
Покажем это. Пусть в некоторой точке согласно принципу суперпозиции 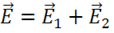
Найдем
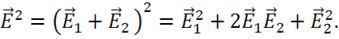
Тогда 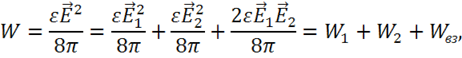
где 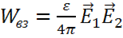 — энергия взаимодействия, причем энергия взаимодействия может быть положительна, отрицательна или равна нулю, но не превышает энергии поля. Покажем это. Рассмотрим
— энергия взаимодействия, причем энергия взаимодействия может быть положительна, отрицательна или равна нулю, но не превышает энергии поля. Покажем это. Рассмотрим 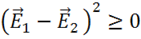 или
или 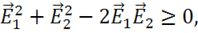 или
или 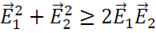 , что соответствует
, что соответствует
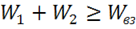 .
.
Это же свойство имеется и для магнитной энергии.
2) Вектор плотности потока электромагнитной энергии — вектор Умова-
Пойнтинга 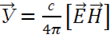 означает, что энергия электромагнитного поля распространяется в пространстве. Материальным носителем энергии является электромагнитное поле. Вся жизнь на Земле обязана энергии Солнца, а доставляется она на Землю электромагнитными волнами!
означает, что энергия электромагнитного поля распространяется в пространстве. Материальным носителем энергии является электромагнитное поле. Вся жизнь на Земле обязана энергии Солнца, а доставляется она на Землю электромагнитными волнами!
П. Л. Капица в статье "Энергия и физика" (см. книгу "Эксперимент, теория, практика") отмечал большое значение теоремы Умова-Пойнтинга в связи с предлагаемыми проектами получения электромагнитной энергии. Незнание теоремы Умова-Пойнтинга превращало некоторые предлагаемые проекты в "прожекты", технически неосуществимые в масштабах страны.
§ 7. Граничные условия для нормальных и касательных составляющих
векторов электромагнитного поля
План:
I. Необходимость граничных условий. Переходный слой.
II. Граничные условия для нормальных составляющих векторов электромагнитного поля.
III. Граничные условия для касательных составляющих векторов электромагнитного поля.
I. Граничные условия в электродинамике играют двоякую роль:
1) это дополнительные условия, так как при интегрировании уравнений Максвелла появляются произвольные постоянные интегрирования и введение дополнительных условий позволяет их определить для конкретного случая.
Аналогичная ситуация имеется и в классической механике. Вспомните, например, движение тела под действием силы тяжести. В зависимости от
дополнительных условий, а в механике, как правило, это начальные значения положения и скорости тела, получается различное по характеру движение.
2) это условия, позволяющие ограничивать область пространства, в которой рассматривается данное поле.
В электродинамике существует проблема — на границе между двумя средами может происходить скачок характеристик среды 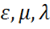 . Это может
. Это может
приводить к тому, что векторы поля на границе терпят разрыв. Чтобы обойти эту трудность сначала вместо границы выбирают переходный слой. В переходном слое характеристики среды меняются непрерывно от значений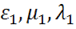 , до
, до 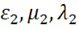 . Проведя необходимые преобразования, для перехода к границе высоту (толщину) переходного слоя устремляют к нулю и получают граничные условия.
. Проведя необходимые преобразования, для перехода к границе высоту (толщину) переходного слоя устремляют к нулю и получают граничные условия.
В электродинамике используются два типа граничных условий — для нормальных составляющих, т. е. для проекций векторов на нормаль к поверхности, и для касательных составляющих, т. е. для проекций на касательное
направление ![]() При этом вектор нормали
При этом вектор нормали ![]() направлен в сторону перехода
направлен в сторону перехода
от 1-й среды ко 2-й (рис. 13).
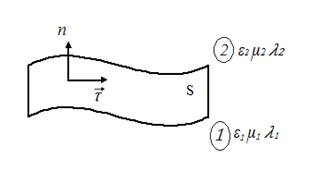
Рис. 13. Векторы ![]() и
и 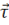 к поверхности раздела
к поверхности раздела
2 а) Граничные условия для нормальных составляющих вектора электрической индукции.
Выберем в переходном слое цилиндр, частично заходящий в первую и вторую среды. Основания цилиндра ![]() и
и ![]() равны
равны ![]() — поверхности на границе
— поверхности на границе ![]() в окрестности точки А. (Рис. 14).
в окрестности точки А. (Рис. 14).
 Рис. 14 Цилиндр в переходном слое
Рис. 14 Цилиндр в переходном слое
Нормали ![]() и
и ![]() и общая нормаль
и общая нормаль ![]() на границе
на границе ![]() указаны на рисунке 14.
указаны на рисунке 14.
Для любой точки поля внутри цилиндра записываем 4-е уравнение Максвелла:
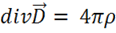
Интегрируем уравнение по объему цилиндра:
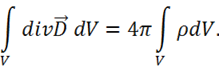
По 1-й теореме Остроградского-Гаусса получаем:
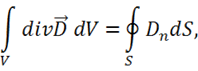
при этом 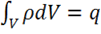 , где
, где ![]() — заряд, находящийся внутри цилиндра.
— заряд, находящийся внутри цилиндра.
Тогда
 (1.65)
(1.65)
Запишем подробно:
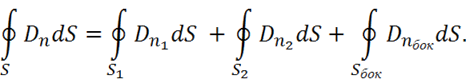
Пусть ![]() и
и ![]() выбраны достаточно малыми, такими, чтобы на каждое из этих поверхностей значение
выбраны достаточно малыми, такими, чтобы на каждое из этих поверхностей значение ![]() было постоянно. Тогда
было постоянно. Тогда
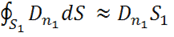
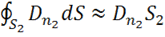 .
.
На боковой поверхности значение ![]() как раз и меняется. Однако по теореме
как раз и меняется. Однако по теореме
о среднем можно преобразовать:
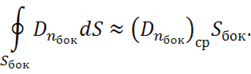
Рассмотрим проекции: 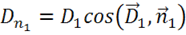 , но поскольку
, но поскольку ![]() и
и ![]() направлены противоположно, то
направлены противоположно, то
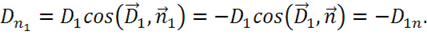
Для ![]() получаем, учитывая, что
получаем, учитывая, что ![]() и
и ![]() направлены в одну строну,
направлены в одну строну,
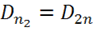 .
.
Тогда
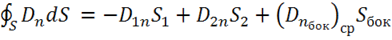
подставим в (1.65) и получим:
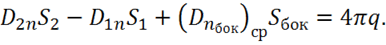 (1.66)
(1.66)
Теперь переходим к границе, это значит, что 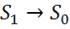 ,
, 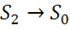 ,
, 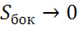 ,
, 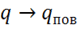 . Тогда получим:
. Тогда получим:
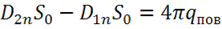 .
.
Разделим на ![]() и введем
и введем 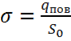 , где
, где ![]() — поверхностная плотность зарядов. Тогда окончательно получим:
— поверхностная плотность зарядов. Тогда окончательно получим:
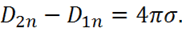 (1.67)
(1.67)
Это и есть искомое граничное условие. Оно означает, что при переходе через границу двух сред нормальная составляющая вектора электрической индукции меняется скачком, если граница заряжена с поверхностной плотностью ![]() . Величина скачка равна:
. Величина скачка равна: 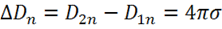 и определяется только значением плотности зарядов на поверхности раздела двух сред и не зависит от свойств этих сред.
и определяется только значением плотности зарядов на поверхности раздела двух сред и не зависит от свойств этих сред.
Если граница не заряжена с поверхностной плотностью, т. е. 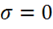 , то скачка нет и нормальная составляющая
, то скачка нет и нормальная составляющая ![]() непрерывна:
непрерывна:
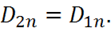 (1.68)
(1.68)
Задание №1. Написать граничные условия для нормальных составляющих вектора электрической напряженности, используя условие (1.67), уравнение
связи 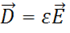 и предполагая, что
и предполагая, что 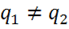 .
.
2 б) Граничное условие для нормальных составляющих вектора магнитной
индукции.
Для получения этого условия можно использовать рисунок 14. Затем, полагая, что во всех точках поля внутри цилиндра выполняется 3-е уравнение Максвелла 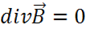 , проводим аналогичные преобразования и получаем:
, проводим аналогичные преобразования и получаем:
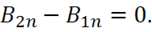 (1.69)
(1.69)
Условие (1.69) означает, что нормальная составляющая вектора магнитной
индукции всегда непрерывна, т. е. 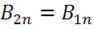 .
.
Задание № 2. Написать граничные условия для нормальных составляющих вектора магнитной напряженности, используя условие (1.69), уравнение связи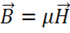 и полагая, что
и полагая, что 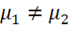 .
.
3 а) Граничные условия для касательных составляющих вектора магнитной
напряженности.
Выберем в переходном слое рамку со сторонами 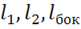 , причем
, причем ![]() и
и ![]() равны
равны ![]() , векторы
, векторы ![]() и
и ![]() направлены так, как показано на рис. 15.
направлены так, как показано на рис. 15.
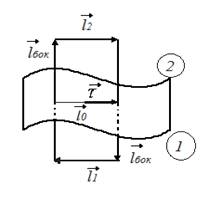 Рис.15. Рамка в переходном слое.
Рис.15. Рамка в переходном слое.
Для любой точки поля внутри рамки записываем 1-е уравнение Максвелла и проектируем его на нормаль ![]() к поверхности рамки:
к поверхности рамки:
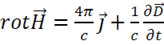 ,
,
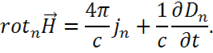
Интегрируем по площади ![]() поверхности рамки и получаем:
поверхности рамки и получаем:
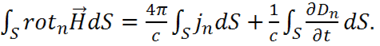 (1.70)
(1.70)
По теореме Стокса преобразуем:
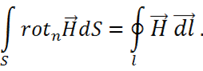
Затем разбиваем интеграл по замкнутому контуру рамки на интегралы по ее сторонам:
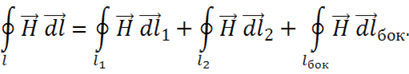 Считая
Считая ![]() и
и ![]() достаточно малыми, получаем:
достаточно малыми, получаем:
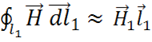 ,
, 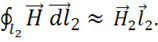
Рассмотрим
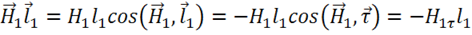 ,
,
при этом учтено, что векторы ![]() и
и ![]() направлены противоположно. Тогда:
направлены противоположно. Тогда:
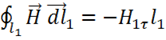 .
.
Аналогично, учитывая, что ![]() и
и ![]() параллельны, получим:
параллельны, получим:
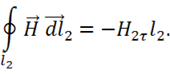
По теореме о среднем преобразуем:
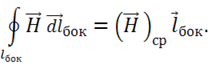
В правой части
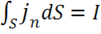 ,
,
где 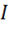 – это сила тока, текущего через площадь
– это сила тока, текущего через площадь ![]() рамки.
рамки.
По теореме о среднем преобразуем:
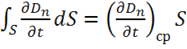 .
.
Тогда вместо (1.70) после всех преобразований получаем:
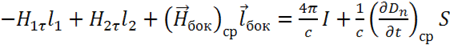 .
.
При переходе к границе 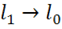 ,
, 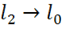 ,
, 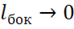 ,
, 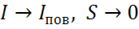 , остается:
, остается:
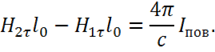
Разделим на ![]() и вводим
и вводим 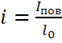 , где
, где 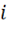 — линейная плотность поверхностного тока. Окончательно получаем:
— линейная плотность поверхностного тока. Окончательно получаем:
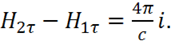 (1.71)
(1.71)
Это и есть искомое граничное условие для касательных составляющих ![]() .
.
(1.71) означает, что если по границе раздела течет поверхностный ток
линейной плотностью, то касательная составляющая ![]() меняется скачком,
меняется скачком,
т. е. 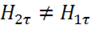 . Величина скачка определяется только значением плотности
. Величина скачка определяется только значением плотности 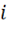 , т. е.
, т. е. 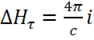 .
.
Если по границе раздела поверхностный ток не течет, то скачка нет, касательная составляющая ![]() непрерывна, т. е.
непрерывна, т. е. 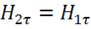 .
.
Это всегда имеет место на границе двух диэлектриков, на границе диэлектрик-вакуум.
Задание № 3. Написать граничные условия для касательных составляющих
вектора магнитной индукции ![]() , используя (1.71) и уравнение связи
, используя (1.71) и уравнение связи 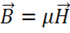 , предполагая, что
, предполагая, что 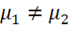 .
.
3. б) Граничное условие для касательной составляющей вектора электрической напряженности ![]() .
.
Используя рис.15 и 2-е уравнение Максвелла 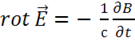 , проводя аналогичные преобразования 3. а), получаем:
, проводя аналогичные преобразования 3. а), получаем:
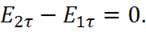 (1.72)
(1.72)
Условие (1.72) означает, что касательная составляющая всегда непрерывна, скачка нет, т. е. 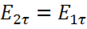 .
.
Задание № 4 . Написать граничные условия для касательных составляющих,
используя условие (1.72) уравнение связи 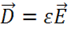 и полагая
и полагая 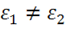 .
.
Задание № 5. После выполнения заданий 1 — 4 составить таблицу всех
граничных условий для нормальных и касательных составляющих векторов 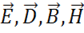 .
.
Глава 11. Электростатика
§ 8. Основные уравнения. Основные задачи электростатики
Электростатика – раздел электродинамики, изучающий поле неподвижных электрических зарядов. Но электрические заряды неподвижны только в одной инерциальной системе отсчета (ИСО). Во всех других ИСО они движутся. Следовательно, все результаты электростатики применимы только к этой одной ИСО. Поскольку заряды неподвижны, 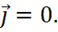 Из уравнения непрерывности (1.40) так как
Из уравнения непрерывности (1.40) так как 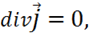 следует
следует 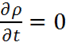 , и
, и 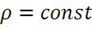 . Кроме того, в статике
. Кроме того, в статике 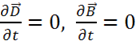 . Тогда уравнения Максвелла (см. §5) примут вид:
. Тогда уравнения Максвелла (см. §5) примут вид:
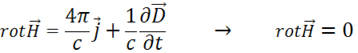
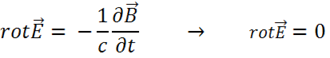
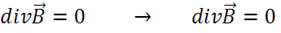
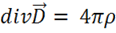
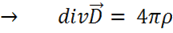 .
.
Эта система уравнений разбивается на две подсистемы, не связанные друг с другом – на электрическую и магнитную:
Электрическая 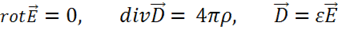
Магнитная
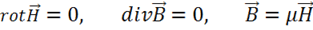
Решение для магнитной системы с учетом граничных условий – тривиальное, т. е. 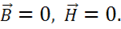 Это означает, что в данной ИСО магнитная компонента электромагнитного поля отсутствует. Однако электрическая компонента есть
Это означает, что в данной ИСО магнитная компонента электромагнитного поля отсутствует. Однако электрическая компонента есть 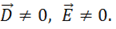 Это и есть электростатическое поле. Оно описывается уравнениями электрической подсистемы. Следовательно, основные уравнения электростатики:
Это и есть электростатическое поле. Оно описывается уравнениями электрической подсистемы. Следовательно, основные уравнения электростатики:



Основные задачи электростатики:
1) Прямая задача – по ![]() найти
найти ![]() и
и ![]() .
.
Решение находим из 4-го уравнения Максвелла (2.2):
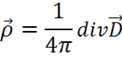
И граничного условия (1.67)
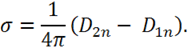
2) Обратная задача — по ![]() и
и ![]() найти
найти 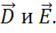 Решается интегрированием (см. § 10).
Решается интегрированием (см. § 10).
3) Найти механические силы, действующие на заряженные тела в электростатическом поле.
§ 9. Основные свойства поля. Скалярный потенциал, его связь с работой.
Уравнение 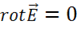 означает, что электростатическое поле безвихревое, имеет незамкнутые силовые линии, связано с зарядами. Силовые линии начинаются на положительных зарядах и кончаются на отрицательных.
означает, что электростатическое поле безвихревое, имеет незамкнутые силовые линии, связано с зарядами. Силовые линии начинаются на положительных зарядах и кончаются на отрицательных.
Основные свойства поля обусловлены его безвихревым характером. Рассмотрим эти свойства.
1) Вычислим работу по перемещению заряда по замкнутому контуру, используя уравнение (2.1) и теорему Стокса:
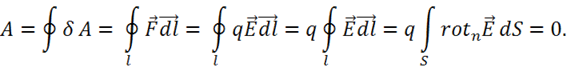
Итак, работа по замкнутому контуру равна нулю: 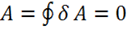
2) Покажем, что работа, совершаемая по перемещению заряда между двумя точками поля, не зависит от формы пути. На рисунке 16 это точки ![]() и D. Указаны два разных пути – через точку K и через точку M.
и D. Указаны два разных пути – через точку K и через точку M.
Требуется доказать, что работа в этом случае одинакова:
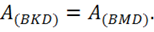
Рис. 16 Замкнутый путь
Докажем это свойство, используя только что доказанное №1.
Согласно свойству 1 работа по замкнутому контуру 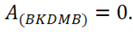 Ее можно разбить на работу из точки
Ее можно разбить на работу из точки ![]() через
через ![]() в точку
в точку ![]() и из точки
и из точки ![]() через точку
через точку ![]() в
в ![]() :
:
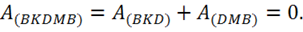
Отсюда
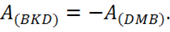
Но работа
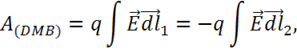
т. к. 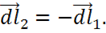 (см. рис. 16)
(см. рис. 16)
А это работа
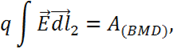
следовательно
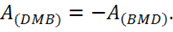
Рассматривая совместно (2.4) и (2.5) получаем
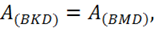
что и требовалось доказать.
Итак, работа, совершаемая по перемещению заряда между двумя точками поля, не зависит от формы пути. Необходимо выяснить, от чего, от какой величины она зависит.
3) Сначала снова используем уравнение 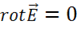 и тождество векторного
и тождество векторного
анализа 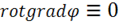 . Уравнение (2.1) удовлетворяется, как видим,
. Уравнение (2.1) удовлетворяется, как видим,
если положить:
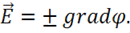
Выберем знак. Для положительного точечного заряда согласно определениям
вектора ![]() и градиента скаляра
и градиента скаляра ![]() имеем в точке М (см. Рис.17)
имеем в точке М (см. Рис.17)
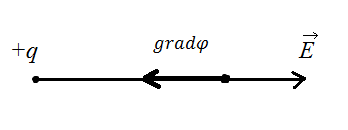 Рис. 17
Рис. 17
Поэтому в дальнейшем е электродинамике всегда полагают:
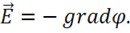 (2.6)
(2.6)
Это основная формула, связывающая вектор ![]() и скаляр
и скаляр ![]() . Необходимо выяснить, что собой представляет введенный таким образом скаляр
. Необходимо выяснить, что собой представляет введенный таким образом скаляр ![]()
4) Для этого найдем элементарную работу, т. е. работу, совершаемую по перемещению единичного положительного заряда на бесконечно малом пути ![]()
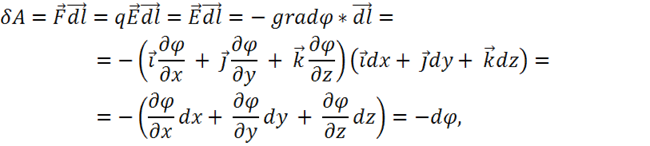
при этом использовались выражения для 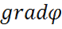 и
и ![]() в декартовых
в декартовых
координатах.
Итак,
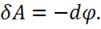 (2.7)
(2.7)
Формула (2.7) означает, что в безвихревом поле элементарная работа
по перемещению единичного положительного заряда – есть полный дифференциал введенного нами скаляра ![]()
5) Найдем, наконец, работу между двумя точками поля, например, точками 1 и 2:
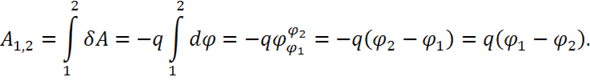
Итак,
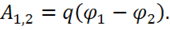 (2.8)
(2.8)
Согласно (2.8) работа зависит от разности значений скаляра ![]() в начале
в начале
и конце пути. Следствия 4) и 5) показывают, что скаляр ![]() характеризует
характеризует
способность поля совершать работу. Поэтому ![]() называется скалярным потенциалом поля или просто потенциалом.
называется скалярным потенциалом поля или просто потенциалом.
В некоторых случаях, если в бесконечности 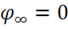 , можно получить
, можно получить
простое определение потенциала. Пусть в формуле (2.8) вторая точка находится в бесконечности. Тогда 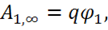 откуда
откуда 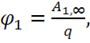
Если 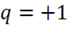 , то
, то
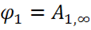 (2.9)
(2.9)
Это означает, что потенциал можно определить как работу, совершаемую
полем по перемещению единичного положительного заряда из данной точки
в бесконечность. Подчеркнем, что такое определение возможно лишь в предположении, что в бесконечности 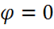 . Реально это соответствует случаям,
. Реально это соответствует случаям,
когда заряженные объекты занимают конечную область пространства. В этом
случае потенциал с увеличением расстояния убывает и можно положить,
что в бесконечности он обращается в нуль.
§10. Дифференциальные уравнения для потенциала, их общие решения.
Нормировка потенциала. Решение 2-й задачи.
Найдем дифференциальные уравнения для потенциала. Для этого запишем
4-е уравнение Максвелла и уравнение связи:
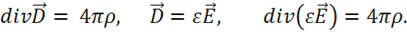
Используем тождество векторного анализа
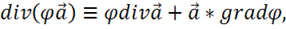
при этом полагая 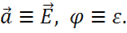
Тогда
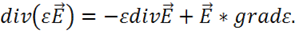
Подставим вместо ![]() из (2.6) выражение для
из (2.6) выражение для ![]()
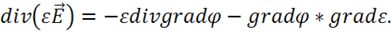
Согласно векторному анализу
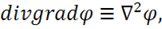
Тогда
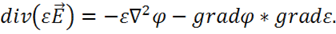
С учетом этих преобразований вместо 4-го уравнения Максвелла получаем уравнение для ![]() :
:
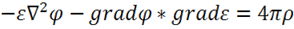
Или разделив обе части уравнения на 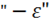 , получим:
, получим:
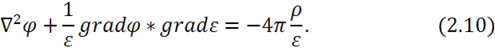
Это дифференциальное уравнение для ![]() в неоднородной среде. Стандартного решения оно не имеет.
в неоднородной среде. Стандартного решения оно не имеет.
Для однородной среды 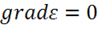 . Тогда вместо уравнения (2.10)
. Тогда вместо уравнения (2.10)
получаем:
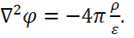
![]()
Это уравнение Пуассона для потенциала ![]() .
.
Если 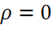 , то получается уравнение Лапласа:
, то получается уравнение Лапласа:

Уравнение Лапласа – однородное дифференциальное уравнение 2-го порядка
в частных производных. Оно описывает потенциал поля вне заряженного
тела в однородной среде. Общее решение уравнения:
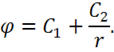
Постоянную интегрирования ![]() можно выбрать в виде
можно выбрать в виде 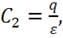 где
где ![]() – заряд тела (см. Приложение III). Тогда:
– заряд тела (см. Приложение III). Тогда:

Постоянную ![]() определим из условия нормировки. Нормировка потенциала – процедура придания однозначности потенциалу. Иначе говоря, выбор определенного значения
определим из условия нормировки. Нормировка потенциала – процедура придания однозначности потенциалу. Иначе говоря, выбор определенного значения ![]() , так как согласно (2.13) и (2.14)
, так как согласно (2.13) и (2.14) ![]() определяется неоднозначно.
определяется неоднозначно.
Как видно из решений (2.13) и (2.14) , ![]() убывает с ростом
убывает с ростом ![]() . Вполне
. Вполне
разумно потребовать, чтобы в бесконечности ![]() обращался в нуль;
обращался в нуль;
если 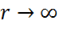 , то
, то 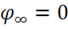 . Тогда для бесконечности имеем:
. Тогда для бесконечности имеем:
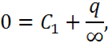
откуда 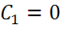 .
.
После нормировки общее решение запишется так:

Формально оно совпадает с потенциалом поля точечного заряда, известного
из курса общей физики.
Решение уравнения Пуассона найдем не строго, чисто качественно.
Для этого разбиваем весь объем ![]() , заряженный с объемной плотностью
, заряженный с объемной плотностью ![]() на элементарные объемы
на элементарные объемы ![]() Причем
Причем ![]() имеет заряд
имеет заряд 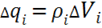 такой, чтобы его можно было считать точечным.
такой, чтобы его можно было считать точечным.
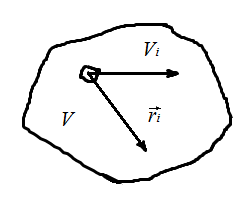 Рис. 18 Объем
Рис. 18 Объем ![]()
Тогда можно применить полученное решение (2.15) для ![]() :
:
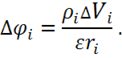
Потенциал от всех элементов ![]() объема
объема ![]() находим по принципу суперпозции:
находим по принципу суперпозции:
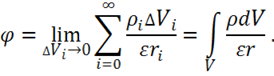
Итак,

Это и есть искомое решение уравнения Пуассона, строго оно получается в курсе "методы математической физики".
Решения (2.15) и (2.16) отличаются при 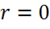 . В самом деле, согласно (2.15)
. В самом деле, согласно (2.15) 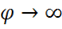 при
при 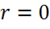 . Это означает, что применять решение (2.15) при
. Это означает, что применять решение (2.15) при 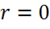 нельзя, нарушается требование точечности заряда.
нельзя, нарушается требование точечности заряда.
Решение (2.16) не расходится при 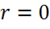 . Рассмотрим решение для
. Рассмотрим решение для ![]() :
:
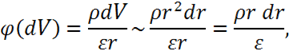
Если ![]() не уменьшается с уменьшением
не уменьшается с уменьшением ![]() .
. ![]() при этом может обращаться в нуль, либо быть постоянным. Так что (2.16) является более общим решением.
при этом может обращаться в нуль, либо быть постоянным. Так что (2.16) является более общим решением.
В электродинамике дискутируется проблема, обусловленная неоднозначностью потенциала, существует две точки зрения:
1) ![]() неоднозначен и поэтому является вспомогательной функцией, никакого
неоднозначен и поэтому является вспомогательной функцией, никакого
физического смысла не имеет.
2) ![]() неоднозначен, но можно придать ему однозначность и физический смысл
неоднозначен, но можно придать ему однозначность и физический смысл
Автор придерживается второй точки зрения.
Отметим, что неоднозначность потенциала не влияет на значение напряженности и работы. В самом деле:
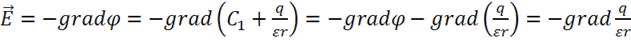 ,
,
т. к. 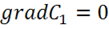
Аналогично для работы находим:
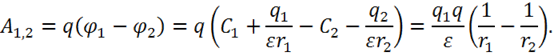
Напряженность и работа имеют одно вполне определенное значение.
К этой проблеме мы будем возвращаться скова в последующих главах.
Теперь учтем все возможные случаи распределения заряда и запишем потенциал:
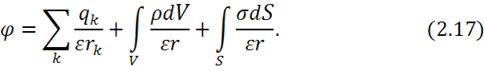
Тогда электрическая напряженность равна:
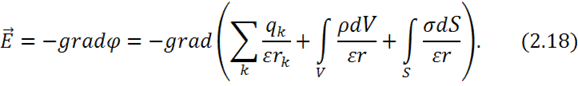
Это и есть решение 2-й задачи электростатики в общем виде.
§ 11. Разложение потенциала системы зарядов на больших расстояниях,
Дипольное, квадрупольное, мультипольное приближения.
Рассмотрим систему точечных зарядов 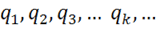 см. (рис. 19):
см. (рис. 19):
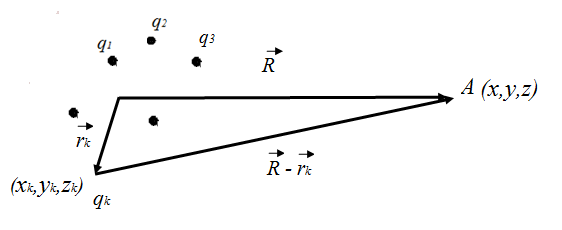
Рис. 19. Система зарядов
Запишем потенциал поля в вакууме для системы точечных зарядов:

Где ![]() — радиус-вектор заряда
— радиус-вектор заряда ![]() ,
, ![]() — радиус-вектор точки наблюдения, отсчитываемые от точки 0, выбранной произвольно внутри системы зарядов.
— радиус-вектор точки наблюдения, отсчитываемые от точки 0, выбранной произвольно внутри системы зарядов.
Если 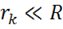 , то
, то ![]() можно разложить в ряд:
можно разложить в ряд:
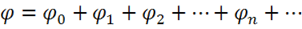
Перед нами стоят две задачи: 1) доказать, что такое разложение возможно,
2) выяснить физический смысл членов разложения.
Сначала займемся первой задачей. В курсе высшей математики изучалось разложение в ряд Тейлора:
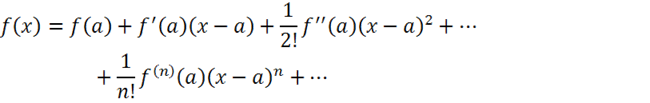
Введем новые обозначения: вместо 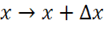 , где
, где 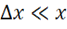 ; вместо
; вместо 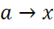 . Тогда
. Тогда  и получим разложение по степеням малой добавки
и получим разложение по степеням малой добавки ![]() :
:
Обобщим это разложение на функцию трех переменных  с малыми добавками
с малыми добавками 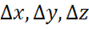 :
:
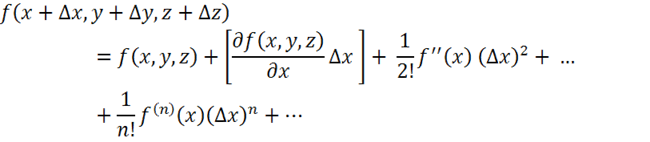
В этом разложении первый член называется нулевым приближением, так как
добавки в нулевой степени, следующие три члена — линейное приближение
с добавками в первой степени, затем девять членов — квадратичное приближение с добавками во второй степени. Теперь понятно, что следующие приближения содержат катастрофически нарастающее число членов /<3. Мы пока ограничимся квадратичным приближением.
Применим написанное разложение (2.21) к (2.19). Введем обозначения:
9 так как Q зависит от ct у, -£ 9 J,
добавки tty^-y*? так как в формуле
^ и v^, входит со знаком "минус". Р2~1£J
Тогда получаем: Л Л ^ ^. ,
Подставим это разложение в (2.19), сразу учитывая и разбивая на соответствующие члены приближения: „
Выражение (2.22) означает, что мы доказали возможность разложения уу. Й
Первая задача формально решена. Но уже в разложении (2.22) видно его преимущество по сравнению с исходным выражением (2.19). В самом деле, согласно (2.19) каждый заряд "сам за себя" дает вклад в потенциал в точке наблюдения А. При решении задач по атому методу пришлось бы учитывать взаимное расстояние каждого заряда до точки А. В разложении (2.22) имеется явное преимущество: отдельными сомножителями входят величины, характеризующие систему зарядов, т. е. заряды ^ и их местоположение, и отдельный сомножитель, который независимо от зарядов характеризует место положение точки наблюдения.
Теперь переходим ко второй задаче — выяснению физического смысла членов разложения (2.22).
Найдем нулевое приближение:
Итак, ‘ ^*23 ^
(2.23) формально совпадает с потенциалом точечного заряда. Поэтому ^0 называют приближением точечного заряда. В нулевом приближении произвольная система зарядов ведет себя как точечный заряд, если i*Oj т. е. система зарядов неэлектронейтральна. При этом суммарный заряд системы как будто находится в точке О, выбранной произвольно.
Рассмотрим линейное приближение:
В этом приближении система зарядов характеризуется вектором р=.Щ9еЪе,
с проекциями /=Х^*-Уг> Р^=*2$*3*} p^-S-?,^ Вектор |5* называется электрическим пли дипольным моментом системы. Это момент первого порядка по
координатам зарядов.
Производные ^ з /</л. D
С учетом сделанных обозначений и введенных понятий получаем;
где использован известный из векторного анализа результат
Итак,
Формально (2.24) совпадает с потенциалом поля диполя и называется поэтому дипольным приближением. В дипольном приближении система зарядов ведет себя как диполь с дипольным моментом j5*_z. 5 ^"zS 1, при этом
дипольный момент системы P как будто расположен в точке 0.
Рассмотрим квадратичное приближение: ^4 . / /;х
В этом приближении система зарядов характеризуется более сложной величиной — моментом второго порядка, причем этот момент имеет 9 компонент.
Это первые сомножители в формуле для — . Эти 9 компонент образуют тензор второго ранга, который называется квадрупольным моментом.
Квадрупольный момент можно записать в виде:
Где (2.26)
Из (2.26) видно, что …
Поэтому тензор jfe.^ имеет 6 разных компонент. В конце темы мы покажем,
что можно уменьшить число компонент до 5 — число независимых компонент.
Теперь перейдем к рассмотрению вторых сомножителей в формуле для г*, •
Вычислим, например, такую производную:
Поскольку ^1ЛЫ(^Щ) — g$
Подставим в производную /
Оставим временно член с — и запишем
Аналогично получайся остальные производные.
Обобщим эту формулу: ^ ,± ^
где — единичные тензор, равный с f / ± о о
« -( ^ X о
Тогда окончательно: * 0 о ^
Счетом ( 2.25 и £2.27^ >j можно компактно записать:
Г£_ называется квадрупольным приближением.
Проведем тождественное преобразование, которое уменьшает число компонент
тензора СЙ^уб до пяти независимых. Для этого сначала раскроем (2.28^) ,
удваивая компоненты согласно свойству тензора: —
Из выраяенриг в квадратных скобках вычтем выражение, тождественно равное
lit*- з ( £Г &) — u
(2.30)
В саном деле (й. ЗО^ можно преобразовать: v2ib2, ?2-
-%г~"7 /ез — ( ^ V
С друге/ стороны можно ^й. ЗСЛболее понятно записать:
+
и сгруппируем ^Ч^/^ПГГ^сА
тле? <
В результате этого преобразования диагональные компоненты тензора
мы простым соотношением, а именно: ^
Сто означает, что одна из диагональные компонент выражается через сую
двух других, взятуЛсо знаком "минус", нацригер,:
Поэтому остается вычислять только п..ть независимых компонент тензора.
Примеры решения задач на квадрупольное приближение (см. Приложение
Определен^ компонент кьадрупольноро момента играет большую роль
в ядерной физике, так как по их значению мо::НО определить фор*гу лдра.
Если ядро имеет сферически-симметричную форму, то все компонентыф^д
Если есть отклонения от с^ергческо’ ‘тугетрпг, то некоторые компонент.
?оменты ‘ олее высокого порядка называется мультипольныыи. Соответс!
но все ра^ло: ение — ля потенциала называется разложением по мультипол!
моментам. Отметим, что уже начиная с квадрупольного приолигения разлс
женив в. гекартовых координатах является неэффективным. Б самом деле i
сначала пришлось записывать девять членов в, но оказалось, что
только пять из них независгмы. ели проводить такое разложение в куб:
ческом приближении — окту> ольном, то в декартовых координатах сначала
пришлось бы записать <7 членов, тогда как анализ показывает, что то.
ко 7 из них независимы.
Имеется (олее рациональное выра ение jyiaf — в сидерических координ
см^Согласно^ . —запишем разло: ение для в форме:
где )ft — Угол MeW £ и ^ ‘
-полином Ле. андра.
Если ввести независимые сферические координаты — углы В и, Sf? и
( индекс iC относится к заряду то п^теореме слдаенил полиномов
Лежандра^ 3 запишем: ( f $
где Sm=jb приЛ1=.0, %h =-1 при fa>0 . При этом полином Лежавд-
ра определяется: ^
а присоединенные полином Лежандра:
С учетом ^2.T’3j и (2*-%) потенциал^можно записать:
Это и есть наиболее рациональное выражение доя разложения потенциала по
мультипольным моментам. 3 самом деле, формула (2.35 )сразу показывает лв
явную зависимость потенциала от расстояния £. до точки наблюдения, мо-
мент соответствующего порядка и число независимых членов в соответствую-
щем приближении. ЦанримСр» см. Таблицу :
Из приведенных примеров членов разложения видно, что на больших
расстояниях основной вклад в потенциал дает *f0 — приближение точечного
заряда, сто и есть оообнование возможности применения в электродинамике
понятия точечного заряда к описанию произвольной системы зарядов, если,
крнечно, ^ ^t^t’D > т. е. система зарядов неэлектронейтраиьнф.!
§ 12. Проводник в электростатическом поле
Проводники имеют свободные, не связанные электрические заряды, т. е.
свободные заряженные частицы. Под действием электростатического поля г
исходит перемещение зарядов на поверхность проводника. Макроскопичеси
описание дает следующие свойства проводника;
i/ Так как в электростатике } — з-о, Х$ по закону Ома дл
проводника при ^внутри проводника — 0 ♦ Вспомните клети
Фарадея!
2/ Соответственно так же Ф а 0 и из 4-го уравнения Максвелла
f~Tfrcttt$^ , т. е. J »- ° . ^
3/ Поскольку 6" s ^^гл^^» но внутри ^"—^ t то^-А^Ус-О иУ=£о
Весь проводник характеризуется одим значением потенциала ^ . Поверхно
проводника является первой эквипотенциальной поверхностью.
4/ Заряды располагаются на поверхности проводника, т. е. (Г^ t> .
5/ Из граничного условия СЗ^-^*и — Verff^t где 10<и^О внутри провод
получаемк пУч^и &xn^*ftr£ » т. е. внешняя напряженность вблизи
поверхности тооводика направлен^ по нормали к поверхности проводика
£jl =. ^£ fr. • При этом учтено, что касательная составляющая
внешней напряженности б5т-=фогласно граничному условию Gxf— £ft~— о**
Достаточно полное описание свойств проводника Q^cm. Тамм И. Е. * £J
Для уединенного проводника заряд на его поверхности мокев быть запи
рде — емкостный коэффициент или просто емкость.
Если имеется несколько проводников, то заряд на одном из них, например
где С*;* при <£^И — емкостныГ: коэффициент, ^
Ск-п при fc^fc — коэффициенты индукции /влияния /.
Например, для двух проводников согласно CS.37) можно запивать:
Если, f^^-p f например, для конденсатора, можно записат
Пусть Yic-O. Складыяая an уравнения при Г, »0 , получаем:
0=^ ^{С, г+Ся1_)ГКУА& при следует: Зьг—<?*4.
Пусть теперь %.-0 , складывая уравнения, получаем: 0— % •fiCju
пщФ4фО следует, что = CjLf. Но следовател
Cfitz&XL S С ^ где О — емкость конденсатора. С- мозг не
найти из первого уравнения, например: Cf^t—^^J Тогда получае
Емкость конденсатора, как известно из курса общей физики, зависит толь
от свойств самого конденсатора.
§ 13. Диэлектрики в электростатическом поле
План
i. Диполь. Потенциал поля диполя.
II. Поляризация диэлектрика. Вектор поляризации.
III. Связь вектора поляризации с плотности) связанных зарядов.
1. Диэлектрики в отличие от проводников имеют связанные заряды. Форма
но диэлектрик можно представить как совокупность^иполей — уже "готовы
т. е. существующих и в отсутствии внешнего поля £"г09 или наведенных —
ду:тированных внешним полем. В макгоскопическоГ электродинамике отвлека
ся от этих деталей. Просто полагают, как мы уже ^ачале отметили, что
диэлектрик состоит из диполей. Поэтому сначала вычислим потенциал поля
диполя. Как известно, диполем называется система из двух разноименных,
одинаковых по величине зарядов. Причем эти заряды расположен компакта
т. е. достаточно близко друг к другу, на расстоянии £ . При стом
вектор £. направлен от — f к ftf .(см. Рис. 20.)
Рис, 20 Диполь. К расчету Рис. 21. Диполь. К расчету
дипольного момента р • потенциала ^.
Согласно общему определению дипольный момент для диполя получаем:
/так, для диполя дипольныР момент равен: ^ =zy<- . От выбора начала
отсчета т. 0 %Р^>не зависит, так как т. О выбрана произвольно.
Вычислим потениЗяал поля диполя в точке наблюдения Си при
Согласно рис. 2i имеем для диполя:
Сделаем приближения: так как Лег ц,, то предположим, что tZ. tfGr’i 9
в знаменателе Ъ-рТ*, ^ ^5. 9 в ^f^tj. — tcMJ- ( • исJ|
Тогда ^ j£c*£ Р^±,^ ^
Итак, потенциал поля диполя равен:
»огмула (^.39)в самом деле совпадает с формуле: (?.24^длл ^ из разд.
жения для потенциала системы зарядов £см. §11 )• ^
11. Рассмотри!*поведение диолектрика во внешнем поле. При £Г* Я диэлект!
полгризуется. ото значит, что объем Av диэлектрика приобретает дипол!
ныР t/омент dj? » которы? можно записать:
где г — вектор, характеризующий поляризацию диэлектрика и называем!
вектором поляризации. Вектор поляризации- определяется как дипольный *
мент единицы объема и равен: ^
*К ;Х % — 6.4.
Для дискретного распределения дипольных моментов ^ вектор поляризации
определяется : ^ Щ;
Я= v
ксперименты показывают, что г* г-* _
где ^/ — коэффициент поляризации данного диэлектрика.
111. }’ы ввели два разных подхода к описанию диэлектрика: Ц с помогц»:
связанных зарядов, которые можно охарактеризовать e-fTCVe объемной
плотностью связанных зарядов^иу и поверхностной плотностью связан
заргдов<^^/ с помощью вектора поляризации Р. Необходимо связать
между собой эти введенные величины.
Сначала предположим, что потенциал поля при наличии диэлектрика
ново представить в виде:
где Td — потенциал внешнего поля в вакууме,
— потеншал поля за счет поляризации диэлектрика.
При гтом (f6 . ^
и аналогично
согласно
С другоР стороны выразим Yf<& через полгризациго Р. Для этого снача
запишем потенциал от элемента объема dV как потенциал поли диполя с д
польным гоменто?.’ ctf ta затем введем вместо otf вектор поляризации
С 2.40) :
Тогда для всего объема диэлектрика получаем:
Преобразуем подинтегтальное выра^енре в у:
? *. ^ т >
причем градиент берете1 по точке источника, лалее используем то: дество
векторного анализа:
J*foa)*№£+&-f"*’P. полагал 0.=Pj •
Тогда тождество получим для /5 и ^ :
откуда; подинтегральное выра ение :
Подставим в (^2.45) t сразу разбивая на два интеграла:
Займемся вторым интегралом в (£.46J. lifc 1-й теореме Остроградского-Га-
усса преобразуем : ^ /Г Л
Но? то преобразование возможно, если внутри осъема у нет поверхносте
разрыва.
Рассмотрим разные случаи,
I. Во всем пространстве, занятом полем, нет поверхносте’/ разрыва [Рц
Тогда мо но применить ^2.47 . Устремим поверхность ^ к ^ф, ох-
ватывающее полное поле, • то ьгачг. т, что па S ВфлО, соответственно
~РzzO • ^то возможно, если заряды расположеня в конечное обласии п{
странства. В самом деле, разложение потенг нала системы зарядов показы-
вает, что самое меменное убвание с расстоянием дает приближение точе*
ного заряда ^ — • Соответственно, напряженность полк £*с*-91а*(
Твевб^Л"^* ПрИ t~a?’t/> &о~>0 9 коне;шо учесть, что i леменз
поверхности dSP&S>m Ц^5~ i^>^ "»о при • при
: том учтено, ЧТО P^~V Eo"^*~l •
Для других приближений будет солее быстрое убывание с увеличением рассто-
яния. Поэтому можно положить:
V
Сравнивая И#4б^ с первым интегралом в Qj.46 J получаем:
2. Пусть внутри och>eua*V~ есть хотя бы одна поверхность разрыва $
на которой Рлу- РчиФ 0 • На внешнее поверхности 5 , окружающей гвйЬра
ны# объем — у, разрыва нет, как и во всем остальном пространстве, заня-
том полем. Зсе "неприятности" сосредоточены внутри данного осъема.
Применим метод, которые успешно используется в электростатике и магнито-
статике. Окру аем поверхность разрыва S/»yf* замкнутоГ поверхностью 3
на котогоС f>i непрерывна. При.-том поверхность S’ .додходит достаточно
слизко к £^ф>.(см. Рис 2с) . Нормаль "Й к Sf*& направлена от 1-:
ко 2-9. среде. Нормали Л1 и ~У{Ь направлены перпендикулярно элементам
oi$<t г cfS^ 9 При этом Si и — С части поверхности ^/ , кото-
рые находятся в 1-й и 2-Р среде соответственно как указано на^Еис.^.
РисД? ПЬвер; ности S; f^U,
Тогда по 1-й теореме истроградского-Гаусса мояно записать:
Первы* интеграл ty^S ^ Ф<*^°?$ "> ° /
ушж в случае 1.,"Ак как все "неприятности") повторимся, содержатся во
ром интеграле. < ян>чпии. 1»и»и^ип ъ*?]^—.нтутралг,
Запишем отдельно второй интеграл:
мы вря Iтом пренебрегли потоком через соковую поверхность, которая мала,
так как £f достаточно ‘лизко подходит к jy^. Их РиСлУвидно, что нор-
маль параллельна нормали JJ, следовательно Рп* = п •
Нормаль f)x аитипараллельна и » следовательно Ро^-Рд^* Устремляя
Тогда
десь мы опустили слово "разрыв", считая, что Л это и есть поверх-
ность, на которой р1Иф Pxvy. Подставим этот результат в^2.4б) :
° V v 5 ^
Сравнивая с VW~ , получаем:
Итак, мы нашли связь вектора поляризации с объемно^ре4^) и поверхност-
но" (бс/л) плотностью связанных заргдов. Ос судим полученные результаты,
i/ Согласно (j^.bO) pcti^^Oi если o/u)p^0 i т. е. елли поляризации неод-
нородна, ото возмог.-но, если внешнеее поле неоднородно, если диэлектрик
неоднороден, ^ если неоднородны? диэлектрик находится в неоднородном поле
X/ Евли etu) ]$я-0 " однородный ди:лектрик в однородном поле, T0Jk(*£r о
I Согласно ^•Sl^^ftntoHa поверхности 3 при p<Y% ^ рлИ
4/ : ели нет скачка ри }, т. е. рщ-аЦ^ то Celtic о
•то Феноменологическое описание, конечно, не раскрывает все многообразие
диэлектриков и их поведение во внешнем поле, /"ля етого необходим более
строги? подход — микроскопическое описание.
§ 14. Энергия в : лектростатике
План
I. энергия глектростатического поля.
II. энергия зарядов, распределенных с объемной и поверхностно!1 плотностью
в поле.
ill. "нергия системы точечных зарядов в поле,
1У. энергия диполя в поле.
#1* — нергия системы точечных зарядов: собственная энергия и энергия взаим
действия.
У*. Энергия диполь-дипольного взаимодействия.
УII. Классический радиус электрона.
I. По теореме Умова-Пойнтинга • нергия электромагнитного поля равна:
Г /. Г£^$i Т§р})Л*’ Я^Д*1 энергия лектростатического поля:
Формула ^<!.5<!) означает, что энергия поля "размазана" по объему V" с
объемной плотностью YVt-jl}rE£iJ? rO. Вея энергия поля согласно
fe*b’d) всегда положительна. I тот вопрос обсу-дался в § 6.
II. Получим энергию зарядов в поле. Для этого вводим ^иы^^ • Тог-
да, подставив эту формулу в, полним:
J — г*
Qbtyuuflf преСразуем согласно то-.деству ^bjP^HJU? &Н4&*ЦА-
согласно
4-му Уравнению : аксвелла, получим: %fl^^-с/^)-У^. одставив
• то выражение в формулу для энергии и сразу разбивая ВДГдм интеграла,
получаем:
На ртом этапе 1нергия имеет вид: .
Второй интеграл в ^«53)яВКМ| преобразовать по 1*1 теореме Остроградского
Гаусса: р р
Но так ‘".е, как И в 9 13 , отметим, что применение ; той теоремы возмож-
но только в случае, если нет поверхностей разрыва подинтегральых функций*
‘-~——• Т. v *^ *1
Рассмотрим два возможных случал.
1. Во всем пространстве, занятом полем, нет поверхностей разрываЯ)ли *f
Тогда Ф Цф„ ~> /<<*Х„^ -*0,
г’Де So — Поверхность, охватывающая полное поле, "ри этом WJbrrofS’** О
при *£.-л^о. Сто возможно, если заряды находятся в конечной области
пространства. Подробны?1 анализ аналогичных выражений мы уже проводили
в § 13. Учтем этот результат и получим вместо выражение для
энергии:
2 £»» одна поверхность взрыва нормальной составляющей вектора элект-
рической индукции, на которой выполняете,- граничное условие Q. G7_p :
‘АУЛ П — wi — ■ —
Скалярный потенциал терпит разрыв при переходе через двойной электричес-
кий слой ( см, нарример, Й. Е. Таил . Но двойные электричес-
кие слои встречаются крайне редко, поэтому в дальнейшем всегда судем
считать }f всюду непрерывным.
Снова, как и в § 13, применим тот же рисунок 22. Тогда запишем:
При этом с интегралом по внешней поверхности S можно поступить, как
в 1-м случае, а именно:
Поэтому остается интеграл по "внутренней" поверхности / t который
приближенно можно записать на в виде суммы двух интегралов — по Sf и S% :
Поскольку (0x4 = —$)fH » так как нормалв /?^и И параллельны,
a — fdjfit так как нормали /?ь и (Г антипараллельны, то
после устремления St ~>$/*лур ■ £t ^^^"bf » получаем:
У Spay, .
Используем граничное условие (1.67 J и записываем:
1^ 4 ^ ‘, где снова опущено
■"слово" разрыв" для поверхности, на которой 0* и=МЭд> Подставим этот
результат в (kJ. oS*) и получим:
v-ijjw * (?.«)
Фордгула /£.55^описываецшнергию зарядов, распределенных с объемно!’:^ ^ и
поверхностной (плотностью, в электростатическом поле, сто потенциаль-
ная энергия заряженного вещества в поле. Вещество в ^.5^ представлен^
плотностями : арядов у к 0* » а поле — потенциалом V • Формула
С3»бб1 ограниченна по сравнение с исходной ) . В самом деле, сог-
ласно ^2»661 энергией обладают только области пространства, в которых
нахолится заряженное вещество. А если вещество не заряжено или его вооб-
ще нет, то энерги’-согласно (2»5.13^равна нулю! Тогда как согласно
(2,52) энергия есть в тан, где вещества нет, а поле есть!
И последнее замечание. Согласно (29ЪЬ ) энергия зависит от% значения
потенциала в некотого" точке, ^то снова подтвешдает точку зрения 2 и
£ и автот>а/ — наличие физического смысла потенциала. Потенциал, таким
образом, является энергетическо; характеристике;’ поля»
ill* ПереГдем теперь к нахождению энергии системы точечных зарядов в поле
а/ 11 ока ем, что для точечных зарядов мо>..но ввести понятие объемной плот-
ности.
Объемная плотность заряда в самом простом случае / равномерное {ко-
предел ение по объекту / равна: » — . J-
I V ‘
Дм точечного заряда f ведет себя "своеооразно", а именно:
р ^ J о° ; в точке, где находится заряд, так какТ=^^.5б)
) / О во всех остальных точках, так как в них^- о,
Дирак преду* о ил использовать для описания $ дельта-функцш.
Дельта-Пункция Дирака:
Г/ 1 f °° > Х = °
Нормировка дельта-пункции — на единицу, т. е. .
ЩЫШ =- i i анаЛогично / f(**«W± I.
Ксли под знаком интеграла кроме или J^r-rf ) находится непрерывная
ХУД’™ /Л / 1 т0 »нтбгр^лы вычисляются очень просто:
лсть функции, которые ведут себя дельта-образно — если они иг/еот острый
максимум. Для них мо>но to>v6 использовать fz^9") .
С учетом свойств дельта-функции Дурака можно ввести понятие объемной плот’
ности зарядов для системы точечных зарядов: ^ —
где ^ характеризует положение заряда ty* ,
У/г-Ъь) ‘ о6об1Дение дельта-функции Дирака на трехмерный случай:
Проверим правильно ли мы ввели / согласно (2.60) Вычислим:
Как и следовало ожидать, получился заряд все£сгстемы зарядов. При втои
использовалась нормировка обобщенной дельта-функции Дирака.
Итак, можно формально описывать систему точечных зарядов с помощью
объемной плотности, но в конце концов бесконечность все-таки появится!
ОиЬеМНиУ! UAS/rnVVlB, nj и ——————
б/ Найдем энергию системы точечных зарядов в поле. Для этого использу-
ем формулу для энергии с £ (2.54^ уведенную по (2.60? и свой-
где использовано свойство С2.59) для трехмерного случая:
Интегрирование ведется по всему пространству
Итак.
(2.61)
Это потенпиальная энергия системы точечных зарядов в поле. При этом по-
ле характеризуется потенциалом *fic в той же точке, в которой находится
заряд ^ • Конечно, эта формула так же ограниченна по сравнению с фор-
мулой ДЛ) энергии поля.
1У. Найдем "полезную" формулу для энергии диполя во внешнем ncjiemif. l^?
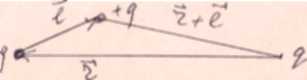
Рис. 23. Диполь во внешнем поле
Б точке ^ находится!. сточиик поля. 11а заряде -"-^ потенциал
заряде — f f. потенциалУ/?7^2 нергия этих зарядов в поле:
Разложим yfttfi) в ряд, считая :
и подставим в энергию: ^ ~* ч
Р! так, энергия диполя во внешнем поле:
гта формула используется г — гиэике для описания поведения диэлектриков
в электрическом поле.
У. Найдем энергию диполь-дипольного взаимодействия, т. е. энергию двух
диполей с моментами Д я. Для этого используем (2.62/ , предпола-
гая, что диполь с моментом fa находится в мле диполя с моментом pt •
Сначала найдем напряженность поля диполя. Пусть
При этом мы использовали тождество векторного анализа
полагая tf=& и <f=(jg* t) Я (>> * ^1
й^векторвог» анализа. Отдельно найдем: ^ХАМ( fi-Zj —
-1* j £ * Ф-
так как ft^Xfifo$i>fel я f не зависит от координат
fXr^-l) точки наблюдения.
Тогда напряженность поля диполя равна:
Подставим (‘г. бз) в формулу Г2.62 % получимrJ ^
2.
у= г* г ‘ (а,
Это и есть энергия диполь-дипольного взаимодействия.
У1 . Находим энергию системы точечных зарядов. Для этого используем
формулу fe.6i? , считая, что потенпиал ^ на заряде создается
той же системой точечных зарядов. Для выделенной пары зарядов(см.
Рис.24): .Ji j
Тогда ■
В
-нергия всех зарядов получится в виде:
тих суммах можно выделить отдельно суммы при ^ и /*^f — if :
Г ^ ^/й’:№«1 2- ****/Г*<ч1 6.66 j
rgjfW$&£*g ^Г^ц Ft*" ?4 — собственная энергия системы точечных
зарядов. Она, как видно, бесконечна. Вот бесконечность и "вылезла",
хотя мы в начале "запрятали" ее в, чях? объемную плотность ^> .
Второй член в /2.65) гавен конечному значению;
iro энергия взаимодействия. Причем, МП W&»>0 , то заряда от-
талкиваются — одноименные, если Л q » ™ заряда притя-
гиваются, —
В обгсем согласно энергия системы точечных зарядов бесконечна,
но в ней есть конечное значение — энергия взаимодействия.
УЛ. Классический радиус электрона.
В современной теоретической физике существует проблема, связанная
с энергией элементарных частиц. Наименьшей частицей вещества является
г-лектррн. Поскольку глектрон заряжен, то его собственная энергия
Vt/’4’^’ , где й — радиус электрона. Можно непосредственными вычисле-
ниям!^" ^см. Приложение Jf показать, что собственная глектростатичес-
кая энергия шара, равномерно заряженного по объему. равна:
С • J
Если электрон — точечная частица, то его собственная энергия бесконечна,
так как &-*0 . Однако согласно СТО к специальная теория относительно-
сти D энергия Ц/=- Мс С | где }rto ~ масса покоя электрона, ота энер-
гия конечна I Следовательно, возникает противоречие электродинамики и
СТО.
Если электрон — протяженная частица радиуса Q, , то его собственая
электростатическая энергия конечна согласно, например, Q2.67J . Но сно-
ва возникает противоречие с СТО. Формула (Х. бЧ) получается в предполо-
жении, что шарик — электрон — абсолютно твердое тело, но согласно СТО
таких тел Сыть не может, иначе это означало бы передачу взаимодействия
с бесконечной скоростью. А согласно СТО предельной скоростью физического
взаимодействия является С — скорость света в вакууме, необходимо от-
метить, чтв проблема взаимодействия элвмх протяженных элементарных час-
тиц до сих пор не решена.
Чтобы "примирить" электродинамику с СТО, в настоящее время предпола-
гают, что элементарные частицы, в том числе электрон, точечные, но
это не радиус частицы, а нижняя граница применимости электродинамики,
на которой она еще не противоречит СТО. <1та нижняя граница получила наз-
вание "классический радиус электрона", хотя никаким радиусом электрона
не является. Находится классический радиус следующим образом: предполар
гаетс. г равенство энергий ■ лектростатической и энергии поко^ электрона:
‘де ^ — классический радиус электрона, равный Qt~*i ‘ СЛ4-
§ 15. Механические силы в электростатике. ~*
Из определения вектора рлектркпеско? напрлтенкостк t слезет, что
для точечного заряда сила равна:
(J2.69)
#Если заряд распределен по объему с плотностью Ф, то можно, вищоляя при-
меняя ^2.69^ к элементу объема<AV с зарядом записать:
где j^pB — объемная плотность силы. В итоге, сила, действующая
на объем Г, равна: р гг
В случае поверхностного распределения зарядов с плотностью о дело
несколько усложняется, так как на поверхности d§ в силу граничных усло-
вий вектор £" неопределен.
Дл^ одного уединенного проводника возникает эффект растяжения его
поверхности, сто объясняется тем, что элементы поверхности заряжены одно-
именномМотталкиваются, но покинуть проводник не могут.
Для проводика, помещенного во внешнее поле, возникает аналогичный эф-
фект. В самом деле, выберем элемент поверхности проводника dS » набо-
ром находятся заряды с плотностю (3-WS ( ?U£ 25 J . Внешнее поле
вблизи поверхности d$ направлено по нормали Тг (дм, § 12 ) , поле £г’
от заряда <Г*с(§ направлено вверх и вниз, поле £п — от всех осталь-
ных элементов поверхности направлено вверх. Все эти векторы, находятся
конечно, вблизи cf$ ив одно!’уточке.
Рис.25. Провод^во нешнем поле.
"F1 этом V r*j? и e^G’+e"-* вне проводника
£Г = С-Р^ б? внутри проводника
Отсюда
Тогда сила, действующая на фпеыент cl£ :
где "btut^ixi*1* tr5*
при этом -$п*( = «мг * " ST0 поверхностнал^плот1 гость механическ*
ких сил, равная осъемно. плотности электростатической) энергии поля. Она
действует по Hopi/али к каждому элементу ct$ • Тогда вся сила может быть
■аписаяа: ~* С / _0 /
Наедем силу, де^ств^^уп на диполь в поле^. Согласно Рис.<;6 в точке,
где находится заряд -~f иапря?.енн^ть_полм, в точке, где нахо-
дите заряд т*-£ шрлмнрост c/^j, Находим результирутптую силу:
Рис.^б. Диполь во внешнем поле.
Разло Bf’t’f-t) I raj,
Подставим это разло — енне в силу г и получаем:
"так, сила, действующая ка диполь, равна:
где оператор fr-Pj = f*Vc ‘
Согласно сила действует на диполь в неоднородно?/; поле в стогону
увелгченда (: . В од1:ородиом поле сила F равна нулю, но действует
момент пары сил F4 — , численно равных, но направленных в разные
стороны. В ежим этот момент.1 , р? 7 т-Zp Ул£7 —
Момент N стремится повернуть диполь так, что(Лг/? совпадало с & . .
Совместным действием момента N и силы объясняется притяжение лег-
ких тел /бумаяек, пылинок и т. п / к наэлектризованным телам. Зтим объяс-
няются эффектные опыты, которые демонстрирует школьный учитель в самом
начале преподавания раздела "электростатика".