ВУЗы по физике
Готовые работы по физике
Как писать работы по физике
Примеры решения задач по физике
Решить задачу по физике онлайнФизика и биофизика методические указания
1. Связь индукции В магнитного поля с напряженностью H:
B = mm0H
где m— магнитная проницаемость среды;
m0 — магнитная постоянная, m0 = 4π·10-7 Гн/м.
2. Напряженность магнитного поля в центре кругового тока
,
где I— сила тока в проводнике;
R — радиус кругового витка.
3. Напряженность магнитного поля, созданного бесконечно длинным прямым проводником с током I на расстоянии а от него:
.
4. Сила Лоренца:
F=qυB sin α
где q — заряд частицы;
υ — ее скорость;
В — индукция магнитного поля.
5. Магнитный поток Ф для однородного магнитного поля и плоского контура площадью S:
Ф = BnS=BS cos α.
6. Работа A по перемещению проводника и контура с током I в магнитном
поле:
А = IDФ,
где DФ — изменение магнитного потока сквозь поверхность, ограниченную контуром.
7. Основной закон электромагнитной индукции:
,
где N — число витков катушки.
8. Электродвижущая сила самоиндукции:
.
где L — коэффициент самоиндукции;
dI/dt — скорость изменения тока в контуре.
9. Энергия магнитного поля тока
.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КОНТРОЛЬНОЙ РАБОТЫ № 1
Пример 1
Тело вращается вокруг неподвижной оси по закону:
φ = A+Bt+Ct2,
где А = 5 рад; B=10 рад/с; С = -1 рад/с2.
Найти полное ускорение точки, находящейся на расстоянии rг = 0,1 м от оси вращения, для момента времени t = 2 с.
Дано:
φ = A+Bt+Ct2 (рад);
r = 0,1 м;
t = 2с;
A = 5 рад; B=10 рад/с: С = -1 рад/с2.
a=?
Решение
Полное ускорение точки может быть найдено как геометрическая сумма тангенциального ускорения аτ, направленного по касательной к траектории, и нормального ускорения ап, направленного к центру кривизны траектории (рис. 1).Запишем: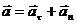 
. Так как векторы аτ и ап взаимно перпендикулярны, то абсолютное значение ускорения:
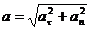. (1)
Тангенциальное и нормальное ускорение точек вращающегося тела выражаются формулами:
аτ = εr, ,
где ε — угловое ускорение тела,
ω — его угловая скорость.
Подставляя выражения для аτ и аn в формулу (1), находим:
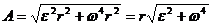. (2)
Угловую скорость ω найдем, взяв первую производную от угла поворота по времени:
.
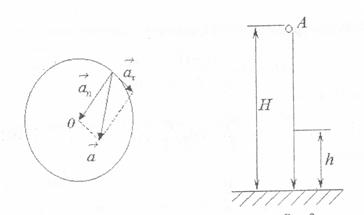
Рис. 1 Рис. 2
Угловое ускорение найдем, взяв первую производную от угловой скорости по времени:
.
Подставляя ω и ε в (2), получим:
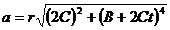(3)
Подставляя в (3) численные значения величин и произведя вычисления, найдем:
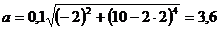м/с2
Ответ: а = 3,6 м/с2
Пример 2
Тело падало с некоторой высоты и последние h = 176,4 м прошло за время t = 2 с. Сколько времени и с какой высоты падало тело?
Дано:
h = 176,4 м;
t = 2c.
t1 = ?
H = ?
Решение
Движение тела равноускоренное с а = g = 9,8 м/с2. Поскольку тело брошено из точки А без начальной скорости (рис. 2), то путь Н, пройденный телом, будет равен:
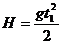, (1)
где t1 — время падения тела.
Путь (H—h) тело прошло за (t1—t) с, следовательно:
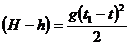. (2)
Подставим (1) в (2):
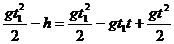(3)
Из (3) найдем:
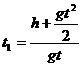(4)
Подставляя в (1) и (4) численные значения величин, найдем t1 и:
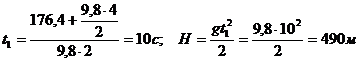
Ответ: t1, = 10 с; Н = 490 м.
Пример 3
Шар массой т1 — 1 кг, движущийся горизонтально с некоторой скоростью х1 столкнулся с неподвижным шаром массой т2 = 4 кг. Шары абсолютно упругие, удар прямой центральный. Какую долю ε своей кинетической энергии первый шар передал второму?
Дано:
v = 0;
т1 = 1 кг;
т2 = 4 кг.
ε =?
Решение
Доля ε энергии, переданной первым шаром второму, выразится соотношением
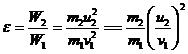(1)
где, W1,v1- кинетическая энергия и скорость первого шара до удара;
W2, v2 — кинетическая энергия и скорость второго шара после удара.
Как видно из (1), для определения ε надо найти u2 . Поскольку удар абсолютно упругий, то выполняются одновременно закон сохранения импульса и закон сохранения энергии. Эти законы с учетом того, что второй шар покоился до удара, имеют вид
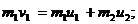(2)
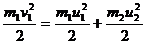
(3)
Решим эти уравнения совместно. Найдем из (2) u1.:
,
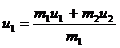и подставим в (3):
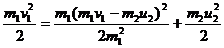(4)
Приведем (4) к общему знаменателю:
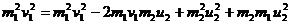(5)
Откуда
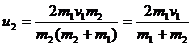(6)
Подставим (6) в (1), получим:
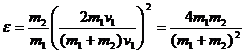(7)
Подставляя в (7) численные значения и произведя вычисления, получим:
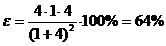
Ответ: ε = 64 %
Пример 4
Маховик в виде сплошного диска радиусом R = 0,5 м и массой 10 кг раскручен до частоты вращения v1 = 240 мин-1 и предоставлен самому себе. Под действием сил трения маховик остановился через 40 с. Найти момент М сил трения.
Дано:
R = 0,5 м;
т = 10 кг;
v1 = 240 мин-1 = 4 с-1; v2 = 0;
t=40 с.
Решение
Для решения задачи воспользуемся основным уравнением вращательного движения:
M = J .ε
где М — момент внешних сил (в нашем случае момент сил трения);
J — момент инерции маховика (в виде сплошного диска), который равен 1/2(mR2);
МГМИМО
Скидка 30% по промокоду Diplom2020
Получи промокод на скидку 20%
Дипломная работа