семинар по квантовой физике
«Физика колебаний и волн. Квантовая физика»
(методические указания к решению задач для студентов 2 курса дневного отделения факультета ИТС потока ИТ(СТ-ПР))
III семестр
1. Интерференция скалярных плоских
монохроматических волн
Явление интерференции заключается в пространственном перераспределении полной интенсивности двух и более волн при их пространственном наложении, которое не сводится к простому сложению интенсивностей. Для двух скалярных волн ψ1 и ψ2 количественное описание интерференционной картины основано на использовании:
1) принципа суперпозиции волновых полей, когда полное волновое поле
|
|
2) определения интенсивности ![]() как квадратичной по волновому полю
как квадратичной по волновому полю ![]() величины, усредненной по времени
величины, усредненной по времени ![]() , где Т – период колебаний полей,
, где Т – период колебаний полей,
|
|
Измеряемой величиной считается интенсивность ![]() , а не само волновое поле
, а не само волновое поле ![]() . Интерференция наблюдается в том случае, если
. Интерференция наблюдается в том случае, если
|
|
При решении задач на расчет стационарной картины интерференции необходимо перейти от ненаблюдаемого распределения волнового поля ![]() к измеряемому распределению интенсивности
к измеряемому распределению интенсивности ![]() и определить положения ее максимумов и минимумов.
и определить положения ее максимумов и минимумов.
Сложение скалярных монохроматических волн заключается в сложении локальных гармонических колебаний, происходящих вдоль одной прямой.
Задача №1
Определить амплитуду А и фазу Ф результирующих колебаний в точке, где осуществляется наложение трех скалярных плоских монохроматических волн с одинаковыми амплитудами а и одинаковыми частотами ω, если фазы колебаний этих волн в данной точке равны Ф1, Ф1+π/2 и Ф1+3π/2. Здесь Ф1=ωt, где t – время.
Решение
При сложении гармонических колебаний, происходящих с одинаковой частотой вдоль одной прямой, удобно использовать метод векторных диаграмм. В этом методе гармонические колебания вдоль, например, оси х
|
|
представляются с помощью вектора ![]() , длина которого равна амплитуде колебаний а, а угол между вектором
, длина которого равна амплитуде колебаний а, а угол между вектором ![]() и осью х в любой момент времени t численно равен фазе колебаний (рис.1)
и осью х в любой момент времени t численно равен фазе колебаний (рис.1)
|
|
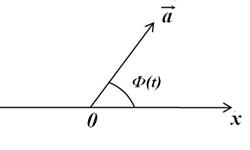
Рис.1
Таким образом, вектор ![]() вращается вокруг точки х = 0 с постоянной угловой скоростью
вращается вокруг точки х = 0 с постоянной угловой скоростью 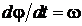 , а его проекция на ось х совершает гармонические колебания с амплитудой а и частотой ω около точки х = 0.
, а его проекция на ось х совершает гармонические колебания с амплитудой а и частотой ω около точки х = 0.
Для сложения двух гармонических колебаний, происходящих с одинаковой частотой вдоль оси х, необходимо из точки х = 0 построить два соответствующих вектора ![]() и
и ![]() в некоторый фиксированный момент времени (например, при
в некоторый фиксированный момент времени (например, при ![]() ). Сумма этих векторов
). Сумма этих векторов
|
|
дает проекцию на ось x, определяющую амплитуду а (длина вектора ![]() ) и фазу Ф(t) (угол между вектором
) и фазу Ф(t) (угол между вектором ![]() и осью х) результирующих колебаний.
и осью х) результирующих колебаний.
В рассматриваемой задаче согласно принципу суперпозиции полное волновое поле ![]() в точке наблюдения
в точке наблюдения
|
|
(1) |
Соответствующая векторная диаграмма трех складываемых гармонических колебаний для момента времени ![]() показана на рис.2.
показана на рис.2.
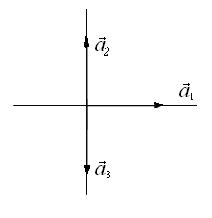
Рис.2
Из рисунка видно, что 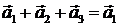 , поэтому для произвольного момента времени результирующие гармонические колебания совпадают с гармоническими колебаниями волнового поля ψ1 как по амплитуде, так и по фазе.
, поэтому для произвольного момента времени результирующие гармонические колебания совпадают с гармоническими колебаниями волнового поля ψ1 как по амплитуде, так и по фазе.
Ответ: амплитуда результирующих колебаний A = a, фаза Ф = Ф1.
Задача №2
При какой разности хода 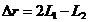 лучей 1 и 2, выходящих из источника S, в точке наблюдения Р: 1) интенсивность излучения максимальная; 2) интенсивность излучения минимальная?
лучей 1 и 2, выходящих из источника S, в точке наблюдения Р: 1) интенсивность излучения максимальная; 2) интенсивность излучения минимальная?
Длина волны обоих лучей одинакова и равна λ. При отражении луча 1 от зеркала М фаза волны увеличивается на π, а интенсивность не меняется. Расположение зеркал и ход лучей показаны на рис. 1.
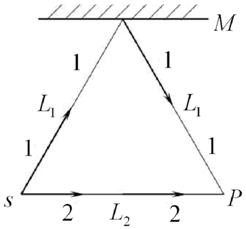
Рис. 1
Решение
Согласно принципу суперпозиции волновое поле в точке наблюдения Р
|
|
(1) |
С помощью векторной диаграммы легко показать, что максимальная амплитуда (и, соответственно, интенсивность) результирующих колебаний получается при разности фаз колебаний
|
|
(2) |
а минимальная амплитуда – при разности фаз
|
|
(3) |
Для плоской монохроматической волны, которую можно использовать для приближенного описания фазы каждого луча, набег фазы при прохождении расстояния r описывается формулой
|
|
(4) |
где волновой вектор ![]() направлен вдоль радиус-вектора
направлен вдоль радиус-вектора ![]() по ходу луча.
по ходу луча.
В соответствии с условиями задачи
|
|
(5) |
поэтому разность фаз складываемых в точке Р гармонических колебаний
|
|
(6) |
Максимальная амплитуда результирующих колебаний наблюдается при
|
|
(7) |
или
|
|
(8) |
а минимальная амплитуда – при
|
|
(9) |
или
|
|
(10) |
Здесь учтено, что для сторон треугольника 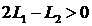 .
.
Следует напомнить, что в результате интерференции происходит локальное увеличение или уменьшение интенсивности полного волнового поля, что связано с пространственным перераспределением интенсивности волны в плоскости наблюдения, где находится точка P. Полная энергия суммарного волнового поля во всем пространстве сохраняется постоянной.
Ответ: интенсивность максимальная, если ![]() ,
,  интенсивность минимальная, если
интенсивность минимальная, если ![]() ,
, 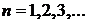 .
.
Задача №3
На плоский экран наблюдения падают две плоские монохроматические скалярные волны, имеющие одинаковые амплитуду а, частоту ν и начальную фазу Ф0 = 0. Волновые векторы ![]() и
и ![]() волн лежат в плоскости хоz, образуют угол α с нормалью к плоскости экрана и ориентированы симметрично относительно этой нормали (см. рис. 1). Фазовая скорость волн υ. Найти ширину
волн лежат в плоскости хоz, образуют угол α с нормалью к плоскости экрана и ориентированы симметрично относительно этой нормали (см. рис. 1). Фазовая скорость волн υ. Найти ширину ![]() интерференционных полос, наблюдаемых на экране в плоскости хоу.
интерференционных полос, наблюдаемых на экране в плоскости хоу.
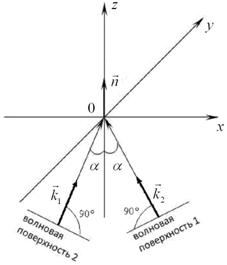
Рис. 1
Решение
Согласно принципу суперпозиции полное волновое поле ![]() в плоскости наблюдения хоу запишется в виде
в плоскости наблюдения хоу запишется в виде
|
|
(1) |
где
|
|
(2) |
|
|
(3) |
Данные формулы позволяют найти характеристики колебаний полного волнового поля сразу во всех точках экрана наблюдения.
Подставляя выражения (2) и (3) в (1), получим:
|
|
(4) |
Здесь использована известная тригонометрическая формула
|
|
Согласно (4) амплитуда колебаний суммарного волнового поля
|
|
(5) |
теперь зависит от координаты х. График зависимости А(х) приведен на рис. 2.
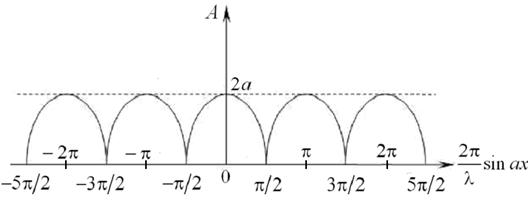
Рис.2
Амплитуда колебаний принимает минимальное значение 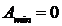 в точках
в точках
|
|
(6) |
где 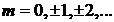 и принимает максимальное значение
и принимает максимальное значение 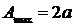 в точках
в точках
|
|
(7) |
где 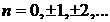 .
.
Шириной интерференционной полосы называется расстояние Δ между соседними интерференционными минимумами или максимумами:
|
|
(8) |
При ![]()
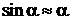 и ширина интерференционных полос
и ширина интерференционных полос 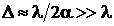 . Это позволяет путем измерения ширины интерференционной полосы найти длину волны видимого света
. Это позволяет путем измерения ширины интерференционной полосы найти длину волны видимого света ![]() с помощью обычной линейки, если
с помощью обычной линейки, если 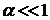 . Иными словами, явление интерференции преобразует длину волны в ширину интерференционной полосы с коэффициентом увеличения
. Иными словами, явление интерференции преобразует длину волны в ширину интерференционной полосы с коэффициентом увеличения 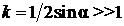 .
.
Ответ: 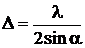 .
.
2. Дифракция скалярной плоской монохроматической волны в приближении Фраунгофера
Задача о распространении волны при наличии в пространстве каких-либо объектов есть дифракционная задача. Решение дифракционных задач базируется на моделях волнового распространения в пустом пространстве и взаимодействия волны с объектом. При решении рассматриваемых ниже задач распространение волны описывается с помощью принципа Гюйгенса-Френеля, а все объекты считаются непрозрачными. Отражение и рассеяние волн на поверхности объектов не учитываются.
Пусть монохроматическая волна распространяется в пустом пространстве. В некоторый момент времени t1 выберем волновую поверхность S1, где во всех точках пространства фаза волны Ф = Ф1 = const. Для каждой точки этой поверхности амплитуда, частота и фаза колебаний считаются известными. В момент времени ![]() выбранная волновая поверхность есть S2 и занимает новое положение в пространстве. Задача заключается в том, чтобы найти амплитуду, частоту и фазу колебаний во всех точках поверхности S2.
выбранная волновая поверхность есть S2 и занимает новое положение в пространстве. Задача заключается в том, чтобы найти амплитуду, частоту и фазу колебаний во всех точках поверхности S2.
Принцип Гюйгенса-Френеля сводит задачу дифракции к интерференционной задаче (рис. 4.1.) Согласно принципу Гюйгенса-Френеля каждый бесконечно малый элемент ![]() исходной волновой поверхности S1 можно рассматривать как вспомогательный источник вторичных волн
исходной волновой поверхности S1 можно рассматривать как вспомогательный источник вторичных волн ![]() . Результирующее волновое поле в любой точке Р волновой поверхности S2 равно сумме всех вторичных волн, пришедших от вспомогательных источников в эту точку,
. Результирующее волновое поле в любой точке Р волновой поверхности S2 равно сумме всех вторичных волн, пришедших от вспомогательных источников в эту точку,
|
|
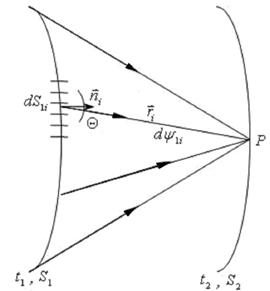
Рис. 2.1.
Для сложения вторичных волн необходимо задать их характеристики. В общем случае каждая вторичная волна есть сферическая монохроматическая волна с центром в точке нахождения соответствующего элемента ![]() волновой поверхности S1. Амплитуда этой волны пропорциональна амплитуде волны, пришедшей от источника в точку нахождения элемента волновой поверхности, и площади
волновой поверхности S1. Амплитуда этой волны пропорциональна амплитуде волны, пришедшей от источника в точку нахождения элемента волновой поверхности, и площади ![]() этого элемента. Кроме того, амплитуда вторичной волны зависит от угла θ между вектором внешней нормали
этого элемента. Кроме того, амплитуда вторичной волны зависит от угла θ между вектором внешней нормали ![]() к элементу поверхности и направлением на точку наблюдения Р. С ростом угла θ амплитуда вторичной волны уменьшается и обращается в нуль, когда θ = π. Частота вторичных волн равна частоте волны, пришедшей от источника. Начальная фаза вторичных волн равна фазе волны, пришедшей от источника в рассматриваемый элемент поверхности S1. В точке Р сложения всех вторичных волн каждая волна имеет дополнительный набег фазы
к элементу поверхности и направлением на точку наблюдения Р. С ростом угла θ амплитуда вторичной волны уменьшается и обращается в нуль, когда θ = π. Частота вторичных волн равна частоте волны, пришедшей от источника. Начальная фаза вторичных волн равна фазе волны, пришедшей от источника в рассматриваемый элемент поверхности S1. В точке Р сложения всех вторичных волн каждая волна имеет дополнительный набег фазы 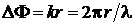 , где r — расстояние от элемента
, где r — расстояние от элемента ![]() до точки Р, — волновое число вторичной волны, λ — длина волны.
до точки Р, — волновое число вторичной волны, λ — длина волны.
Объект на пути распространения исходной волны, идущей от источника, просто исключает из суммы определенные вспомогательные источники вместе с их вторичными волнами, которые не попадают в точку наблюдения Р в силу непрозрачности объекта. В результате излучения вторичных волн незакрытыми вспомогательными источниками возникает огибание волной непрозрачного объекта.
Необходимо отметить, что дифракция – отклонение от закона прямолинейного распространения – наблюдается не только при наличии непрозрачных объектов, но и в пустом пространстве. Для этого необходимо, чтобы распределение интенсивности на волновой поверхности излучения было неоднородным.
Характер интерференции в точке наблюдения Р зависит от соотношения между длиной волны λ, линейным размером b объекта, на котором происходит дифракция, и расстоянием ![]() между объектом и точкой наблюдения Р. Если волновой параметр
между объектом и точкой наблюдения Р. Если волновой параметр
|
|
распределение волнового поля в достаточно малой области наблюдения можно приближенно описывать как суперпозицию вторичных плоских монохроматических волн. Это приближение называется приближением Фраунгофера, а дифракция – дифракцией Фраунгофера. При этом приходящие в точку наблюдения плоские монохроматические волны можно приближенно считать распространяющимися в одном направлении, поэтому дифракцию Фраунгофера называют также дифракцией в параллельных лучах.
Рассмотрим дифракцию плоской монохроматической волны, падающей нормально на плоский непрозрачный экран, в котором имеется прямая щель шириной b >> λ, где λ — длина волны (см. рис. 4.2.). Данное условие необходимо для того, чтобы излучение свободно проходил через щель. Непрозрачный экран Э с щелью находится в плоскости хоу. Щель расположена параллельно оси у. Расстояние между экраном с щелью и плоскостью наблюдения П равно L.
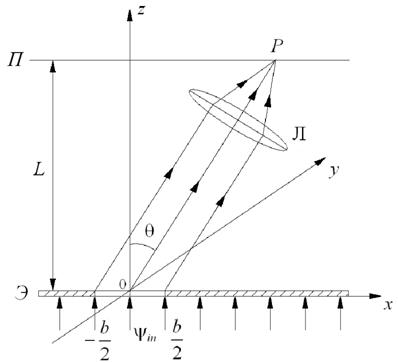
Рис. 2.2.
Точка наблюдения Р задается с помощью угла θ. Параллельные вторичные лучи, идущие от поверхности щели 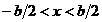 , собираются в точке Р с помощью фокусирующей линзы Л.
, собираются в точке Р с помощью фокусирующей линзы Л.
Волна, падающая на экран с щелью, имеет вид:
|
|
где А > 0 – постоянная амплитуда, 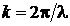 ,
, 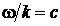 ,
,  . Предполагается, что волновой параметр
. Предполагается, что волновой параметр
|
|
поэтому задачу можно решать в приближении Фраунгофера.
Все вторичные волны на плоскости щели имеют одинаковые частоту, амплитуду и начальную фазу. В точке наблюдения Р приходящие вторичные волны отличаются только набегом фазы
|
|
где ΔФ(0) — набег фазы вторичной волны, приходящей от центрального элемента щели, 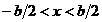 .
.
Параллельные вторичные плоские волны (лучи) собираются в точке Р с помощью фокусирующей линзы Л. Суммарное волновое поле находится путем суммирования всех вторичных волн с учетом разности набега фазы
|
|
где с – постоянная, одинаковая для всех вторичных волн.
Соответствующая интенсивность описывается выражением
|
|
где 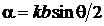 и
и ![]() — максимальная интенсивность дифрагированной волны при угле наблюдения θ = 0. График зависимости
— максимальная интенсивность дифрагированной волны при угле наблюдения θ = 0. График зависимости ![]() приведен на рис.4.3. Дифракционная картина представляет собой чередование светлых и темных полос, расположенных параллельно щели в экране.
приведен на рис.4.3. Дифракционная картина представляет собой чередование светлых и темных полос, расположенных параллельно щели в экране.
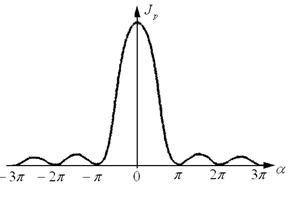
Рис. 2.3.
а) Положения дифракционных минимумов (темные полосы) определяются следующими углами:
|
|
или
|
|
где использованы соотношения
|
|
б) Положение главного дифракционного максимума (центральная светлая полоса) соответствует углу наблюдения
|
|
Здесь используется известный предел
|
|
Другие дифракционные максимумы описываются формулами
|
|
или
|
|
Отметим, что на центральный дифракционный максимум приходится свыше 90% всей энергии волны, прошедшей через щель.
Задача №4
Постройте график зависимости угловой ширины Δθ главного (центрального)дифракционного максимума от ширины b щели в непрозрачном плоском экране для случая нормального падения на экран плоской монохроматической волны с длиной волны λ.
Решение
Согласно определению угловая ширина главного дифракционного максимума
|
|
(1) |
монотонно уменьшается с увеличением ширины щели. Соответствующий график зависимости угловой ширины главного дифракционного максимума от ширины щели ![]() приведен на рис. 1. Если ширина щели b < λ, эффективность прохождения воны через щель резко уменьшается, а формулы,
приведен на рис. 1. Если ширина щели b < λ, эффективность прохождения воны через щель резко уменьшается, а формулы,
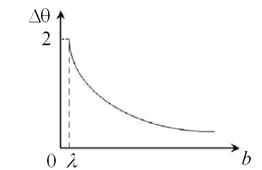
Рис. 1
определяющие положения дифракционных минимумов и максимумов (за исключением главного дифракционного максимума), становятся неприменимыми.
Отметим, что если для получения интерференции используются дифрагированные волны, идущие от щелей в экране, интерференционную картину обычно можно наблюдать только в пределах их общего главного дифракционного максимума.
Задача №5
Плоская монохроматическая волна с длиной волны λ нормально падает на непрозрачный плоский экран с двумя параллельными щелями шириной b, находящимися на расстоянии d друг от друга. При каком условии дифракционный минимум первого порядка (m=1) совпадает с интерференционным максимумом порядка m? Ширина щели ![]() .
.
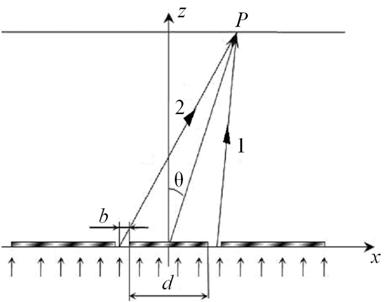
Рис. 1
Решение
Будем считать, что наблюдение ведется в дальней зоне дифракции, где справедливо приближение Фраунгофера. Распределение интенсивности ![]() на экране наблюдения z = L определяется пространственным наложением интерференционной и дифракционной картин, поскольку наблюдается интерференция дифрагированных волн, идущих от щелей.
на экране наблюдения z = L определяется пространственным наложением интерференционной и дифракционной картин, поскольку наблюдается интерференция дифрагированных волн, идущих от щелей.
Рассчитаем интерференционную картину. Две щели рассматриваются как когерентные источники вторичных плоских монохроматических волн, приходящих в точку наблюдения Р с разностью хода
|
|
(1) |
поэтому их разность фаз
|
|
(2) |
Интерференционные максимумы (светлые полосы) наблюдаются в точках Р, где
|
|
(3) |
Интерференционные минимумы (темные полосы) наблюдаются в точках Р, где
|
|
(4) |
Если считать, что интенсивность интерферирующих волн не зависит от угла наблюдения θ, то интерференционная картина представляет собой чередование одинаковых по ширине светлых и темных параллельных полос. Соответствующее распределение интенсивности ![]() показано на рис.1, где
показано на рис.1, где ![]() .
.
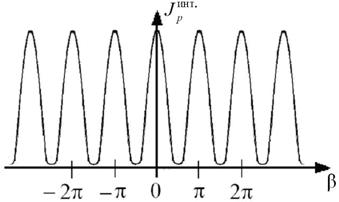
Рис. 1
Однако интенсивность каждой волны, дифрагированной на щели, зависит от их угла распространения θ согласно формуле
|
|
(5) |
Распределение интенсивности ![]() дифрагированной волны (5), приведенное на рис. 2, модулирует интерференционное распределение интенсивности на рис. 1. В результате наблюдаемая интенсивность волны для любого угла θ не превышает
дифрагированной волны (5), приведенное на рис. 2, модулирует интерференционное распределение интенсивности на рис. 1. В результате наблюдаемая интенсивность волны для любого угла θ не превышает 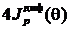 , а распределение интенсивности интерференционных полос лежит между осью α и кривой интенсивности
, а распределение интенсивности интерференционных полос лежит между осью α и кривой интенсивности ![]() .
.
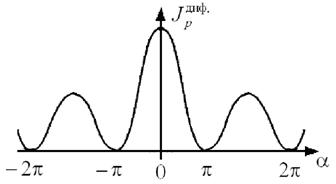
Рис. 2
Согласно условиям задачи
|
|
(6) |
Отсюда находим, что должно выполняться условие
|
|
(7) |
Под углом, определяемым формулой (6), наблюдается темная полоса, поскольку в эту область не попадают дифрагированные лучи.
Ответ: 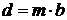 .
.
Задача №6
Как изменится интерференционная картина, наблюдаемая при нормальном падении плоской монохроматической волны на непрозрачный плоский экран с двумя длинными прямыми и параллельными щелями, если 1) расстояние d между щелями увеличить в 2 раза; 2) ширину b каждой щели уменьшить в 2 раза? Наблюдение ведется в дальней зоне дифракции.
Решение
Расстояние d между щелями определяет ширину Δ наблюдаемых интерференционных полос
|
|
(1) |
а ширина b щели – линейный размер l главного дифракционного максимума на экране наблюдения
|
|
(2) |
Здесь λ – длина волны и L – расстояние между экраном с щелями и плоскостью наблюдения.
Интерференционные полосы наблюдаются только в области главного дифракционного максимума, где видность интерференционных полос достаточно высокая, поэтому можно считать, что полное N число наблюдаемых интерференционных полос описывается формулой
|
|
(3) |
При увеличении расстояния d в два раза и постоянной величине b ширина интерференционных полос уменьшится в два раза, а размер главного дифракционного максимума не изменится. Следовательно, полное число интерференционных полос увеличится в два раза.
Если ширину b каждой щели уменьшить в два раза, то размер главного дифракционного максимума увеличится в два раза, а ширина интерференционных полос при неизменном расстоянии d останется постоянной. Таким образом, полное число интерференционных полос снова увеличится в два раза.
Ответ: 1) ширина интерференционных полос уменьшится в два раза, размер главного дифракционного максимума не изменится, число наблюдаемых интерференционных полос увеличится в два раза; 2) ширина интерференционных полос не изменится, размер главного дифракционного максимума увеличится в два раза, число наблюдаемых интерференционных полос увеличится в два раза.
3. Внешний фотоэффект и эффект Комптона
В классической физике электромагнитное излучение есть непрерывное в пространстве и времени распределение векторов напряженностей электрического 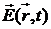 и магнитного
и магнитного ![]() полей, проявляющих себя посредством взаимодействия с заряженными частицами вещества. Это взаимодействие описывается с помощью силы Лоренца
полей, проявляющих себя посредством взаимодействия с заряженными частицами вещества. Это взаимодействие описывается с помощью силы Лоренца
|
|
где ![]() — заряд частицы и
— заряд частицы и ![]() — скорость частицы.
— скорость частицы.
В квантовой теории электромагнитное излучение рассматривается как совокупность фотонов (квантов), обладающих энергией
|
|
и импульсом
|
|
Здесь 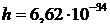 Дж·с — постоянная Планка,
Дж·с — постоянная Планка, 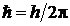 ,
, 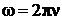 — круговая частота излучения, λ — длина волны,
— круговая частота излучения, λ — длина волны, ![]() — волновой вектор,
— волновой вектор, ![]() — волновое число и
— волновое число и ![]() м/с — скорость света в вакууме. Полное число фотонов определяется энергией электромагнитного излучения. Приведенные выше формулы описывают фотоны плоской монохроматической волны.
м/с — скорость света в вакууме. Полное число фотонов определяется энергией электромагнитного излучения. Приведенные выше формулы описывают фотоны плоской монохроматической волны.
Из формулы Эйнштейна
|
|
связывающей энергию Е, импульс частицы ![]() и массу m частицы, следует, что масса фотона равна нулю.
и массу m частицы, следует, что масса фотона равна нулю.
Электромагнитное излучение можно рассматривать как объект, одновременно обладающий волновыми свойствами, которые проявляются в таких явлениях как интерференция и дифракция, и корпускулярными свойствами, которые обнаруживаются при взаимодействии электромагнитного излучения с веществом. Волновые и корпускулярные свойства излучения не противоречат, а дополняют друг друга, позволяя выбрать наиболее удобный и адекватный способ описания того или иного физического явления.
В случае взаимодействия электромагнитного излучения с веществом, когда происходит поглощение, излучение или рассеяние этого излучения, квантовая теория описывает элементарные акты взаимодействия отдельного фотона с отдельным атомом или электроном. В каждом таком элементарном акте выполняются законы сохранения энергии, импульса и момента импульса, если фотон электромагнитного излучения и взаимодействующая с ним частица вещества образуют замкнутую систему.
Создание квантовой теории электромагнитного излучения опиралось на такие опытные факты, которые классическая теория Максвелла не могла полностью объяснить и количественно точно описать. К этим опытным фактам относятся внешний фотоэффект, открытый Г. Герцем в 1887 г., и эффект Комптона, открытый А. Комптоном в 1922 г..
Экспериментальная схема для наблюдения внешнего фотоэффекта, приведенная на рис.7.1, включает в себя вакуумный диод D, состоящий из стеклянного баллона, из которого откачан воздух, и находящихся в этом баллоне металлических катода К и анода А, источник постоянной ЭДС ![]() , соединенный электрической цепью через сопротивление R с катодом К и анодом А, и внешний источник электромагнитного излучения, которое через стенки баллона может попадать на поверхность катода. Внешний фотоэффект заключается в том, что при определенных условиях в случае попадания на поверхность катода электромагнитного излучения в данной цепи возникает постоянный электрический ток.
, соединенный электрической цепью через сопротивление R с катодом К и анодом А, и внешний источник электромагнитного излучения, которое через стенки баллона может попадать на поверхность катода. Внешний фотоэффект заключается в том, что при определенных условиях в случае попадания на поверхность катода электромагнитного излучения в данной цепи возникает постоянный электрический ток.
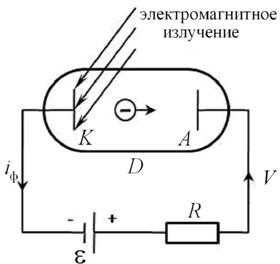
Рис.3.1
Если нет электромагнитного излучения, то в вакуумном диоде отсутствуют носители электрического тока и цепь постоянного тока является разомкнутой. В этом случае ток по цепи не течет несмотря на то, что внутри диода существует постоянное электрическое поле, направленное от положительно заряженного анода А к отрицательно заряженному катоду К.
Если включить внешний источник электромагнитного излучения и направить это излучение на поверхность металлического катода, то при выполнении определенных условий электроны проводимости катода, поглощая электромагнитное излучение, могут вылетать с поверхности катода и таким образом становиться носителями тока в вакуумном диоде. Зависимость протекающего в цепи фототока iф от постоянного напряжения V, поданного на диод, для случая постоянной интенсивности электромагнитного излучения показана на рис.7.2.
Максимальный фототок iф. т. при 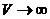 называется током насыщения. Его величина, определяемая мощностью поглощенного излучения, растет с увеличением мощности электромагнитного излучения.
называется током насыщения. Его величина, определяемая мощностью поглощенного излучения, растет с увеличением мощности электромагнитного излучения.
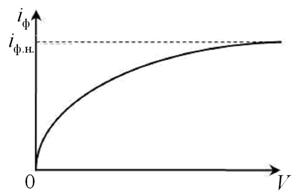
Рис.3.2
Основы квантовой теории внешнего фотоэффекта были заложены А. Эйнштейном в 1905 г., который применил закон сохранения энергии к элементарному акту поглощения фотона свободным электроном проводимости металла. Уравнение Эйнштейна для внешнего фотоэффекта имеет вид:
|
|
Согласно закону сохранения энергии энергия ![]() поглощенного фотона полностью передается электрону и частично идет на совершение работы выхода
поглощенного фотона полностью передается электрону и частично идет на совершение работы выхода ![]() электрона из металла, а другая часть энергии остается у электрона, вылетевшего с поверхности металла, в виде его кинетической энергии
электрона из металла, а другая часть энергии остается у электрона, вылетевшего с поверхности металла, в виде его кинетической энергии 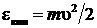 на достаточно большом расстоянии от поверхности металла.
на достаточно большом расстоянии от поверхности металла.
В классической теории работа выхода совершается против сил, удерживающих электрон внутри металла. Этими силами являются кулоновские силы притяжения между отрицательно заряженным электроном и положительно заряженными ионами кристаллической решетки металла, электрическое поле которых на время вылета электрона локально оказывается не скомпенсированным.
Задача №7
Работа выхода электрона для никеля 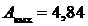 эВ. Определить длину волны
эВ. Определить длину волны ![]() излучения, соответствующую так называемой красной границе внешнего эффекта. Красная граница на оси длин волн определяется максимальной длиной волны, при которой еще возможен внешний фотоэффект.
излучения, соответствующую так называемой красной границе внешнего эффекта. Красная граница на оси длин волн определяется максимальной длиной волны, при которой еще возможен внешний фотоэффект.
Решение
Задача решается с помощью уравнения Эйнштейна для внешнего фотоэффекта
|
|
(1) |
Красная граница определяется условием
|
|
(2) |
в соответствии с которым для электромагнитного излучения с длинами волн 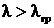 внешний фотоэффект не наблюдается.
внешний фотоэффект не наблюдается.
Из уравнения (2) получаем, что
|
|
(3) |
При расчете необходимо перевести электрон-вольты в джоули: 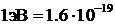 Дж.
Дж.
Ответ: 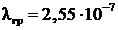 м.
м.
Задача №8
Определить максимальную скорость ![]() электрона, вылетающего с поверхности медного электрода, который освещается электромагнитным излучением с длиной волны
электрона, вылетающего с поверхности медного электрода, который освещается электромагнитным излучением с длиной волны 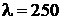 нм. Работа выхода электрона для меди
нм. Работа выхода электрона для меди 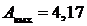 эВ. Масса электрона
эВ. Масса электрона ![]() кг.
кг.
Решение
Задача решается на основе уравнения Эйнштейна для внешнего фотоэффекта
|
|
(1) |
Отсюда получаем, что
|
|
(2) |
Ответ: 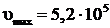 м/с.
м/с.
Эффект Комптона относится к процессу рассеяния электромагнитных волн на свободных электронах, где в результате взаимодействия меняется направление распространения электромагнитной волны. Классическая электродинамика описывает рассеяние как результат излучения электронов, совершающих вынужденные колебания на частоте падающей электромагнитной волны под действием ее электрического поля. Вследствие этого частота рассеянного излучения должна совпадать с частотой падающей электромагнитной волны. Тщательные измерения длины волны рассеянного излучения, выполненные А. Комптоном с сотрудниками, показали, что эта длина волны отличается от длины волны падающего электромагнитного излучения. При этом данное различие зависит от угла рассеяния, т. е. угла между направлениями распространения падающей и рассеянной волнами.
Описанный эффект, получивший имя Комптона, может быть легко объяснен с помощью квантовой теории на основе законов сохранения энергии и импульса замкнутой системы, состоящей из фотона и свободного электрона. Допустим, что до взаимодействия свободный электрон покоился. Благодаря взаимодействию с электроном налетающий фотон рассеивается и летит в новом направлении под углом θ к его начальному направлению (рис.7.3).
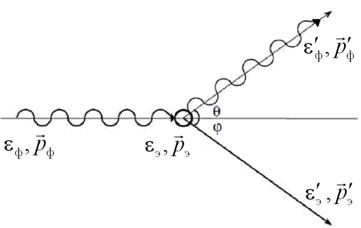
Рис.3.3
Законы сохранения энергии и импульса для элементарного акта взаимодействия фотона и электрона запишутся в виде:
|
|
Здесь нештрихованные величины относятся к фотону и электрону до процесса рассеяния, а штрихованные величины относятся к фотону и электрону после их взаимодействия. В случае первоначально покоящегося электрона 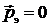 .
.
Решение приведенной выше системы уравнений как в нерелятивистском, так и в релятивистском случае дает одинаковое выражение для длины волны ![]() фотона, рассеянного под углом θ,
фотона, рассеянного под углом θ,
|
|
где ![]() и величина
и величина
|
|
называется комптоновской длиной волны электрона.
Поскольку для электрона величина ![]() очень мала, то для наблюдения эффекта Комптона используется коротковолновое рентгеновское излучение. В этом случае относительное изменение
очень мала, то для наблюдения эффекта Комптона используется коротковолновое рентгеновское излучение. В этом случае относительное изменение ![]() длины волны рассеянных фотонов становится экспериментально наблюдаемым.
длины волны рассеянных фотонов становится экспериментально наблюдаемым.
Задача №9
Фотон с длиной волны 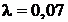 нм рассеивается на свободно покоящемся электроне под углом
нм рассеивается на свободно покоящемся электроне под углом 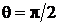 . Определить долю энергии
. Определить долю энергии 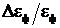 , потерянной фотоном, и скорость
, потерянной фотоном, и скорость ![]() электрона, полученную им в результате рассеяния фотона.
электрона, полученную им в результате рассеяния фотона.
Решение
Согласно основной формуле для эффекта Комптона
|
|
(1) |
поэтому доля энергии, потерянной фотоном,
|
|
(2) |
Здесь использовано, что ![]() . Относительная погрешность приведенного расчета
. Относительная погрешность приведенного расчета 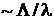 .
.
На основе закона сохранения импульса можно записать, что
|
|
(3) |
или
|
|
(4) |
и
|
|
(5) |
поскольку угол рассеяния θ = π/2 и 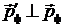 Из (5) следует, что
Из (5) следует, что
|
|
(6) |
Здесь используется нерелятивистская формула для импульса электрона, поскольку 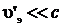 .
.
Ответ: 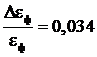 ,
, 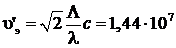 м/с.
м/с.
4. Частица в потенциальной яме
Свободное движение частицы в пустом пространстве, где во всех точках потенциальную энергию частицы можно положить равной нулю, описывается следующим нестационарным уравнением Шредингера
|
|
где ψ — волновая функция частицы, 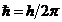 ,
, 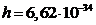 Дж·с — постоянная Планка, m – масса частицы.
Дж·с — постоянная Планка, m – масса частицы.
Простейшее решение этого уравнения, соответствующее стационарному состоянию частицы с энергией Е и импульсом ![]() , имеет вид:
, имеет вид:
|
|
где С – нормировочная постоянная, и называется волной де Бройля. Согласно уравнению Шредингера энергия Е и импульс свободной частицы ![]() связаны между собой хорошо известным соотношением нерелятивистской механики
связаны между собой хорошо известным соотношением нерелятивистской механики
|
|
По аналогии с плоской монохроматической волной волну де Бройля можно записать следующим образом
|
|
где ![]() ,
, 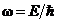 , и ввести длину волны де Бройля
, и ввести длину волны де Бройля
|
|
Длина волны де Бройля есть характерный пространственный масштаб квантовых явлений для частицы с массой m и энергией E в микромире. Если размер пространственной области, где протекает физический процесс, порядка или меньше длины волны де Бройля, то для его описания необходимо использовать законы квантовой физики.
Задача №10
Определить длину волны де Бройля ![]() для электрона, протона и частицы массой
для электрона, протона и частицы массой 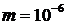 кг, движущихся с одинаковой скоростью
кг, движущихся с одинаковой скоростью 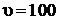 м/с. Масса электрона
м/с. Масса электрона ![]() кг, масса протона
кг, масса протона ![]() кг, постоянная Планка
кг, постоянная Планка ![]() Дж·с.
Дж·с.
Решение
Используя формулу для длины волны де Бройля
|
|
(1) |
получаем, что для электрона
|
|
(2) |
для протона
|
|
(3) |
и для частицы
|
|
(4) |
Отметим, что в случае макроскопической частицы длина волны де Бройля ![]() на много порядков меньше линейных размеров самой частицы, что исключает практическую необходимость применения законов квантовой физики для описания её движения.
на много порядков меньше линейных размеров самой частицы, что исключает практическую необходимость применения законов квантовой физики для описания её движения.
Ответ: 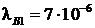 м,
м, 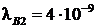 м,
м, 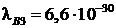 м.
м.
Задача №11
Определить энергию E стационарных состояний частицы массой m в бесконечно глубокой прямоугольной потенциальной яме шириной L (см. рис.1). Чему равна величина средней скорости ![]() , с которой частица движется внутри потенциальной ямы?
, с которой частица движется внутри потенциальной ямы?
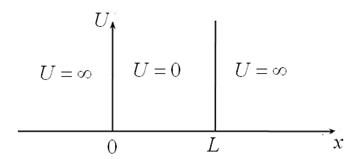
Рис. 1
Решение
Запишем стационарное уравнение Шредингера для частицы с массой m и энергией E, движущейся в потенциальном поле ![]()
|
|
(1) |
Отметим, что в отличие от законов движения классической динамики частицы уравнение (1) не содержит силу, действующую на частицу.
В областях ![]() и
и ![]() , где потенциальная энергия частицы бесконечно большая, вероятность нахождения частицы с любой конечной энергией
, где потенциальная энергия частицы бесконечно большая, вероятность нахождения частицы с любой конечной энергией ![]() равна нулю, поэтому следует положить
равна нулю, поэтому следует положить
|
|
(2) |
если ![]() или
или ![]() .
.
Для определения энергии Е стационарных состояний частицы, т. е. энергии, которая сохраняется постоянной при движении частицы, необходимо решить уравнение
|
|
(3) |
в интервале 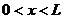 при двух граничных условиях для волновой функции
при двух граничных условиях для волновой функции
|
|
(4) |
Уравнение (3) удобно переписать следующим образом:
|
|
(5) |
где 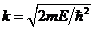 . Решение уравнения (5), удовлетворяющее граничным условиям (4), запишется в виде:
. Решение уравнения (5), удовлетворяющее граничным условиям (4), запишется в виде:
|
|
(6) |
где С – нормировочная постоянная.
Граничные условия (4) выполняются, если
|
|
(7) |
Отсюда находим, что энергетический спектр ![]() частицы в рассматриваемой потенциальной яме описывается выражением
частицы в рассматриваемой потенциальной яме описывается выражением
|
|
(8) |
Это дискретный спектр, т. е. энергия частицы в потенциальной яме квантуется, причем энергия частицы в основном состоянии при ![]() отлична от нуля:
отлична от нуля:
|
|
(9) |
В потенциальной яме частица обладает только кинетической энергией, поэтому согласно (9) частица не может находиться в состоянии покоя и занимать определенное положение в пространстве. Этот вывод справедлив при любом ограничении области возможного нахождения частицы.
По условию нормировки волновой функции
|
|
и
|
|
(10) |
Это условие нормировки означает, что вероятность нахождения частицы в потенциальной яме равна 1.
Полная волновая функция стационарного состояния частицы с энергией ![]() имеет вид:
имеет вид:
|
|
(11) |
В стационарном состоянии (11) среднее значение импульса частицы равно нулю
|
|
(12) |
а среднее значение квадрата импульса отлично от нуля и находится с помощью уравнения
|
|
или
|
|
(13) |
Отсюда можно оценить величину средней скорости, с которой движется частица внутри потенциальной ямы
|
|
(14) |
или
|
|
(15) |
Из формулы (8) видно, что энергетический спектр частицы зависит от геометрического размера ямы L. Этот эффект называется пространственным квантованием и используется для управления энергетическим спектром наноструктур с линейными размерами порядка 10нм. Такие структуры, ограниченные в трехмерном пространстве, называются квантовыми точками и применяются, например, для создания одноэлектронных транзисторов.
Ответ: 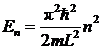 ,
, 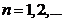 ;
; 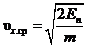 .
.
Задача №12
Оценить эффективную температуру ![]() нулевых колебаний в основном состоянии гармонического осциллятора с частотой собственных колебаний
нулевых колебаний в основном состоянии гармонического осциллятора с частотой собственных колебаний ![]() рад/с .
рад/с .
Решение
Из решения стационарного уравнения Шредингера следует, что энергетический спектр механического гармонического осциллятора с потенциальной энергией
|
|
(1) |
где k > 0 – постоянная, m – масса частицы, 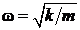 – частота собственных колебаний осциллятора и х – смещение частицы относительно ее устойчивого положения равновесия х = 0, является дискретным и эквидистантным:
– частота собственных колебаний осциллятора и х – смещение частицы относительно ее устойчивого положения равновесия х = 0, является дискретным и эквидистантным:
|
|
(2) |
Эквидистантность энергетического спектра означает независимость разности 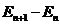 энергий соседних уровней от номера n.
энергий соседних уровней от номера n.
Энергия основного состояния гармонического осциллятора при n = 0
|
|
(3) |
есть энергия случайного хаотического движения частицы, которое называется нулевыми колебаниями. Это квантовое движение не прекращается даже при абсолютном нуле температуры.
Еще раз отметим, что кинетическая энергия частицы, находящейся в ограниченной области пространства, всегда отлична от нуля.
Эффективная температура определяется формулой
|
|
(4) |
где 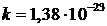 Дж/К — постоянная Больцмана. Таким образом, кинетическая энергия движения частицы в основном состоянии даже при абсолютном нуле температуры Т=0К согласно законам квантовой механики на порядок больше средней кинетической энергии теплового движения той же частицы при комнатной температуре
Дж/К — постоянная Больцмана. Таким образом, кинетическая энергия движения частицы в основном состоянии даже при абсолютном нуле температуры Т=0К согласно законам квантовой механики на порядок больше средней кинетической энергии теплового движения той же частицы при комнатной температуре 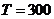 К.
К.
Ответ: 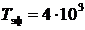 .
.
Атомы вещества в конденсированном состоянии совершают гармонические колебания вблизи своих равновесных положений и поэтому обладают отличной от нуля энергией при T=0К. По порядку величины эта энергия нулевых колебаний
|
|
где M – масса атома и d – диаметр области, приходящейся на один атом. Для атома He4 M=6,64·10-27кг, 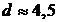 Å и E0=1,6·10-22Дж, что соответствует эффективной температуре Tэф=10К. Поскольку взаимодействия атомов гелия на расстоянии порядка d относительно невелико, то даже при понижении температуры до 0,001К жидкий гелий не затвердевает, если давление ниже 30 атмосфер. Это связано с квантовым движением атомов гелия при низкой температуре. С повышением давления расстояние между атомами гелия уменьшается и приводит к более быстрому росту энергии их взаимодействия по сравнению с энергией нулевых колебаний, что в конечном итоге обуславливает переход гелия в твердое состояние.
Å и E0=1,6·10-22Дж, что соответствует эффективной температуре Tэф=10К. Поскольку взаимодействия атомов гелия на расстоянии порядка d относительно невелико, то даже при понижении температуры до 0,001К жидкий гелий не затвердевает, если давление ниже 30 атмосфер. Это связано с квантовым движением атомов гелия при низкой температуре. С повышением давления расстояние между атомами гелия уменьшается и приводит к более быстрому росту энергии их взаимодействия по сравнению с энергией нулевых колебаний, что в конечном итоге обуславливает переход гелия в твердое состояние.
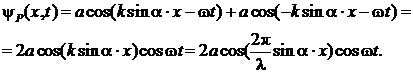
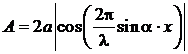
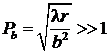 ,
,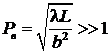 ,
,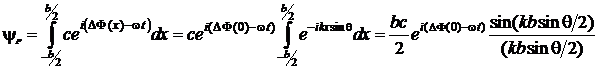 ,
,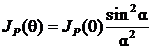 ,
,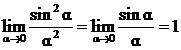 .
.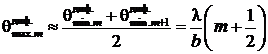 ,
, 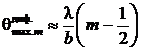 ,
, 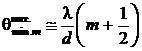 ,
, 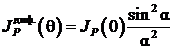 ,
, 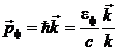 .
.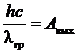 ,
,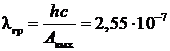 м.
м.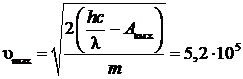 м/с.
м/с.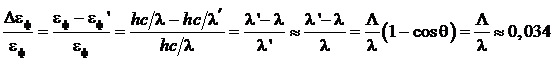 .
.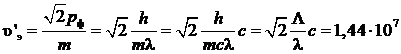 м/с.
м/с.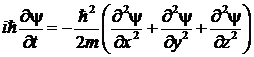 ,
,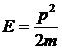 .
.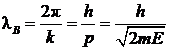 .
.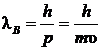 ,
,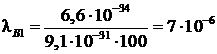 м,
м,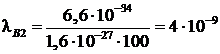 м,
м,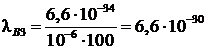 м.
м.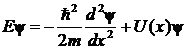 .
.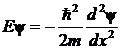
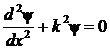 ,
,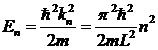 ,
, 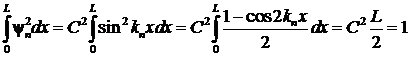
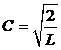 .
.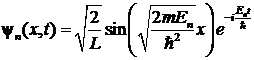 ,
, 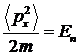
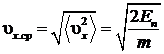 .
.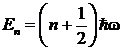 ,
, 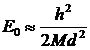 ,
,

