Геометрические характеристики плоских сечений

В определённом масштабе откладываем значения и , соединяем полученные точки прямыми линиями, так как при действии сосредоточенных внешних сил перемещения линейно зависят от абсцисс сечений стержня, и получаем график (эпюру) перемещений (рис. 9е). Из эпюры видно, что некоторое сечение D–D не перемещается. Сечения, расположенные выше сечения D–D , перемещаются вверх (стержень сжимается); сечения, расположенные ниже, перемещаются вниз (стержень растягивается).

Вопросы для самоконтроля

1. Как вычисляются значения продольной силы в поперечных сечениях стержня?

2. Что представляет собой эпюра продольных сил и как она строится?

3. Как распределены нормальные напряжения в поперечных сечениях центрально-растянутого (сжатого) стержня и чему они равны?

4. Как строится эпюра нормальных напряжений при растяжении (сжатии)?

5. Что называется абсолютной и относительной продольной деформацией? Их размерности?

6. Что называется жёсткостью поперечного сечения при растяжении (сжатии)?

8. Как формулируется закон Гука?

9. Абсолютная и относительная поперечные деформации стержня. Коэффициент Пуассона.

10. Что называется допускаемым напряжением? Как оно выбирается для пластичных и хрупких материалов?

11. Что называется коэффициентом запаса прочности и от каких основных факторов зависит его величина?

12. Назовите механические характеристики прочности и пластичности конструкционных материалов.

3. Геометрические характеристики плоских сечений

3.1. Статические моменты площади

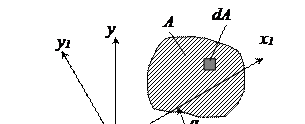
Пусть имеется сечение произвольной формы (рис. 10). Статическими моментами площади А относительно осей x, y соответственно называются интегралы по площади сечения вида:

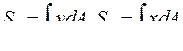(3.1)

Размерность этих характеристик – линейный размер в кубе (мм3, см3, м3).

Через введённые понятия статических моментов определяется центр тяжести сечения – точка Ос с координатами :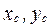

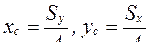. (3.2)

Оси координат хсОсус, проходящие через центр тяжести сечения, называются центральными осями. Статические моменты площади сечения относительно центральных осей равны нулю .

Оси симметрии площади сечения являются центральными осями.

На практике часто приходится рассматривать сложные сечения, состоящие из нескольких простых фигур. Статический момент сложного сечения относительно некоторой оси равен алгебраической сумме (статические моменты отверстий в сечение принимаются со знаком минус) статических моментов отдельных частей сечения, определённых относительно этой же оси. В этом случае координаты центра тяжести сложной фигуры находят по формулам:

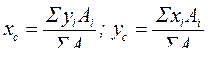, (3.3)

где Ai, xi, yi – соответственно площадь и координаты центра тяжести каждой из составляющих фигур (i = 1, 2 ,… п);

п – число фигур.

Для определения центра тяжести сложной фигуры необходимо:

1. Выбрать систему координат xOy.

2. Разбить сложное сечение на части, имеющие вид простых фигур (прямоугольник, треугольник, полукруг и т. д.).

2. Определить площади и положения (координаты) центров тяжести простых фигур относительно осей выбранной системы координат.

3. По формулам (3.1) вычислить статические моменты каждой фигуры относительно x и y.

4. Алгебраическим суммированием (статические моменты фигур, являющиеся отверстием, берутся со знаком минус) определить суммарные статические моменты.

5. Определить общую площадь сечения (площади отверстий вычитаются)

6. По формулам (3.3) определить координаты центра тяжести сечения.

При параллельном переносе осей координат (рис. 11) статический момент площади изменяется на величину, равную произведению площади сечения на расстояние между осями:

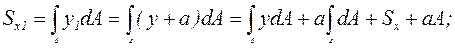(3.4)

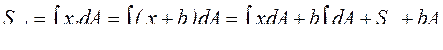. (3.5)

Статические моменты возрастают с увеличением расстояния от центральных осей, относительно которых они равны нулю.

3.2. Моменты инерции сечения

Осевыми моментами инерции сечения (рис. 3.1) относительно осей x, y называются интегралы вида:

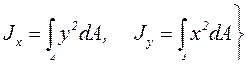. (3.6)

Осевые моменты инерции всегда положительные.

Центробежный момент инерции сечения относительно осей x, y представляет собой интеграл вида:

. (3.7)

Центробежный момент инерции может быть положительным, отрицательным или равным нулю. Если сечение имеет ось симметрии, то центробежный момент инерции относительно координатных осей, одна из которых есть ось симметрии, равен нулю.

Полярный момент инерции сечения определяется интегралом вида:

, (3.8)

где ρ − расстояние от начала принятой системы осей координат до элементарной площадки dA ,

поэтому полярный момент инерции сечения есть сумма осевых моментов инерции:

. (3.9)

Размерность моментов инерции – линейный размер в четвёртой степени (мм4, см4, м4).

Осевые моменты инерции площади сложного сечения относительно некоторой оси равны алгебраической (моменты инерции фигур отверстий в сечении принимаются со знаком минус) сумме осевых моментов инерции отдельных частей сечения, определённых относительно этой же оси.

При параллельном переносе осей координат (в случае, если исходные оси координат – центральные (рис. 12)) моменты инерции относительно новых осей равны:

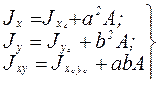, (3.10)

где – моменты инерции сечения относительно центральных осей .

Минимальные значения моментов инерции получаются относительно центральных осей.

Моменты инерции произвольного сечения при повороте системы координат на угол α изменяются (рис. 13). Оси, относительно которых осевые моменты инерции принимают экстремальные значения, а центробежный момент равен нулю, называются главными. Осевые моменты относительно главных осей называются главными моментами инерции. Главные оси, проходящие через центр тяжести сечения, называются главными центральными.

Положение главных осей относительно произвольной первоначальной системы координат определяется углом α0, определяемым по формуле:

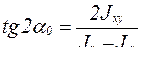. (3.11)