Индивидуальное задание по гидравлике
Индивидуальные задания по гидрогазодинамике с методическими указаниями для студентов очного и очно-заочного обучения по направлению 280700 «Техносферная безопасность» (квалификация бакалавр) по двум профилям: «Безопасность технологических процессов и производств» и «Инженерная защита окружающей среды»
Санкт-Петербург
Общие указания
В настоящих методических указаниях приведены задания по дисциплине «Гидрогазодинамика» для студентов специальности БТП и ЗОС.
Для каждой задачи дано по двадцать пять вариантов цифровых исходных данных. Номер варианта сообщается студенту преподавателем. Это может быть номер, под которым в журнале записана фамилия студента.
При выполнении заданий необходимо соблюдать следующие требования:
1. Работа пишется от руки чернилами на одной стороне листа. Страницы должны быть пронумерованы.
2. Решение задач вести с пояснением каждого хода решения.
3. Перед вычислением искомых величин следует вначале написать исходную формулу в буквенном выражении, дать пояснение всем входящим в нее параметрам, затем представить их численные значения и привести окончательный ответ.
4. У всех размерных величин должна быть поставлена размерность в Международной системе единиц СИ.
5. Значение всех коэффициентов следует обосновать ссылкой на литературу.
6. Чертежи к работе должны выполняться на миллиметровке и вклеиваться в работу.
7. При построении расчетных графиков нужно указать величины, откладываемые по осям графика, с обозначением их размерностей.
8. Все ошибки отмеченные преподавателем, должны быть исправлены, а сделанные указания выполнены. Исправлять ошибки следует отдельно по каждой задаче на чистой стороне листа.
При решении задач необходимо строго следить за соблюдением единства размерностей величин, входящих в ту или иную расчетную зависимость.
Методические указания разработали д. т.н., профессор Штыков В. И., к. т.н., доцент Пономарёв А. Б., к. т.н., доцент Русанова Е. В.
Задача № 1
Закрытый резервуар (рис.1) заполнен жидкостью. Заданы плотность жидкости![]() , избыточное гидростатическое давление на поверхности po, а также размеры «а» и «h».
, избыточное гидростатическое давление на поверхности po, а также размеры «а» и «h».
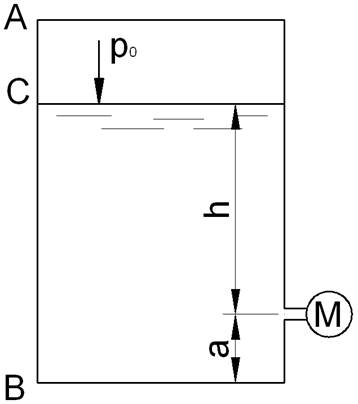
Рис. 1
Требуется определить:
1. Пьезометрическую высоту hp для точки подключения манометра.
2. Показания манометра pм.
3. Абсолютное и избыточное гидростатическое давление на дне резервуара.
4. Построить эпюру избыточного гидростатического давления на стенку АВ.
Табл. 1
|
No вар. |
кг/м3 |
po, кПа |
h, м |
a, м |
No вар. |
кг/м3 |
po, кПа |
h, м |
a, м |
|
1 |
750 |
20 |
3,0 |
2,0 |
14 |
800 |
20 |
1,8 |
2,5 |
|
2 |
800 |
25 |
2,0 |
2,5 |
15 |
700 |
25 |
2,5 |
1,8 |
|
3 |
900 |
30 |
2,5 |
2,8 |
16 |
750 |
15 |
2,8 |
2,0 |
|
4 |
950 |
15 |
2,0 |
3,0 |
17 |
900 |
23 |
1,8 |
2,5 |
|
5 |
1000 |
20 |
2,5 |
2,2 |
18 |
1000 |
20 |
2,0 |
1,8 |
|
6 |
800 |
25 |
3,0 |
2,0 |
19 |
850 |
18 |
2,5 |
2,0 |
|
7 |
750 |
30 |
3,5 |
2,5 |
20 |
900 |
30 |
2,0 |
2,5 |
|
8 |
900 |
15 |
2,0 |
2,0 |
21 |
950 |
20 |
1,8 |
2,2 |
|
9 |
950 |
20 |
1,8 |
2,8 |
22 |
750 |
22 |
3,0 |
1,8 |
|
10 |
850 |
28 |
2,0 |
2,5 |
23 |
700 |
25 |
2,8 |
2,4 |
|
11 |
1000 |
18 |
2,5 |
2,0 |
24 |
1000 |
28 |
2,0 |
2,5 |
|
12 |
950 |
30 |
3,0 |
1,8 |
25 |
950 |
18 |
3,0 |
1,7 |
|
13 |
850 |
28 |
3,5 |
2,8 |
Указания к решению задачи № 1
1. Пьезометрическая высота hp определяется по формуле:
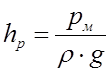
где 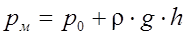 – величина избыточного гидростатического давления в точке подключения манометра. Эта же величина и будет совпадать с показаниями манометра.
– величина избыточного гидростатического давления в точке подключения манометра. Эта же величина и будет совпадать с показаниями манометра.
2. Величина избыточного гидростатического давления на дне будет равна:
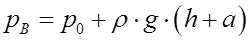
3. Абсолютное гидростатическое давление отличается от избыточного на величину атмосферного давления.
4. Избыточное гидростатическое давление в точке А и К равно Ро. Избыточное гидростатическое давление в точке «B» вычисляется по формуле. От точки «К» до точки «B» гидростатическое давление растет пропорционально заглублению точки под свободной поверхностью. Вид эпюры избыточного гидростатического давления на стенку АВ представлен на рис. 2.
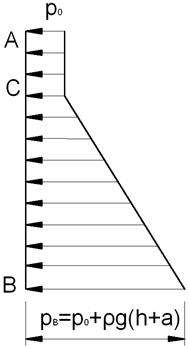
Рис. 2 Вид эпюры избыточного гидростатического давления
Задача № 2
Круглый горизонтальный резервуар (рис. 3), имеющий диаметр D и длину L, заполнен жидкостью, плотность которой ρ. Манометр, установленный на уровне верхней образующей, показывает избыточное давление p.
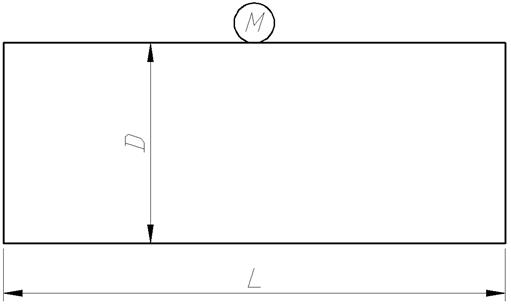
Рис. 3
Требуется определить:
1. Горизонтальную силу Рх, растягивающую резервуар в направлении вдоль рисунка.
2. Расстояние, на которое отстоит линия действия горизонтальной силы от оси резервуара (эксцентриситет).
3. Вертикальную силу Рz, действующую на верхнюю половину резервуара.
Таблица 2.
|
No вар. |
D, м |
p, MПа |
ρ, кг/м3 |
L, м |
No вар. |
D, м |
p, MПа |
ρ, кг/м3 |
L, м |
|
1 |
1,0 |
0,010 |
750 |
3,0 |
14 |
1,5 |
0,010 |
800 |
4,0 |
|
2 |
1,0 |
0,015 |
800 |
3,5 |
15 |
2,0 |
0,025 |
900 |
3,5 |
|
3 |
2,0 |
0,020 |
850 |
4,0 |
16 |
2,5 |
0,020 |
850 |
5,0 |
|
4 |
2,5 |
0,025 |
900 |
4,5 |
17 |
3,0 |
0,035 |
950 |
4,5 |
|
5 |
3,0 |
0,030 |
1000 |
5,0 |
18 |
3,5 |
0,030 |
750 |
5,5 |
|
6 |
3,5 |
0,040 |
950 |
5,5 |
19 |
2,0 |
0,040 |
1000 |
6,0 |
|
7 |
2,0 |
0,045 |
900 |
6,0 |
20 |
1,0 |
0,045 |
750 |
5,0 |
|
8 |
1,0 |
0,050 |
750 |
3,0 |
21 |
3,0 |
0,015 |
800 |
4,5 |
|
9 |
1,5 |
0,020 |
800 |
3,5 |
22 |
1,5 |
0,050 |
900 |
5,5 |
|
10 |
2,5 |
0,030 |
850 |
4,5 |
23 |
2,5 |
0,035 |
850 |
4,0 |
|
11 |
3,0 |
0,035 |
1000 |
4,0 |
24 |
2,0 |
0,015 |
950 |
3,5 |
|
12 |
2,0 |
0,040 |
900 |
5,0 |
25 |
3,5 |
0,050 |
1000 |
3,0 |
|
13 |
1,0 |
0,015 |
1000 |
3,0 |
Указания к решению задачи № 2
Горизонтальная сила Рx, растягивающая резервуар в направлении вдоль рисунка (ось Х на рис. 4), равна силе избыточного гидростатического давления на плоскую торцевую стенку диаметром D и вычисляется по формуле:
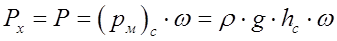
где ![]() – манометрическое или избыточное гидростатическое давление в центре тяжести рассматриваемой плоской фигуры в Па;
– манометрическое или избыточное гидростатическое давление в центре тяжести рассматриваемой плоской фигуры в Па;
ω – площадь данной фигуры, м2;
![]() – глубина погружения центра тяжести рассматриваемой плоской фигуры под пьезометрическую плоскость, если гидростатическое давление внутри резервуара больше атмосферного.
– глубина погружения центра тяжести рассматриваемой плоской фигуры под пьезометрическую плоскость, если гидростатическое давление внутри резервуара больше атмосферного.
Для вычисления 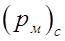 необходимо определить положение пьезометрической плоскости hp, используя выражение
необходимо определить положение пьезометрической плоскости hp, используя выражение
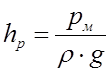
где p – показание манометра, Па.
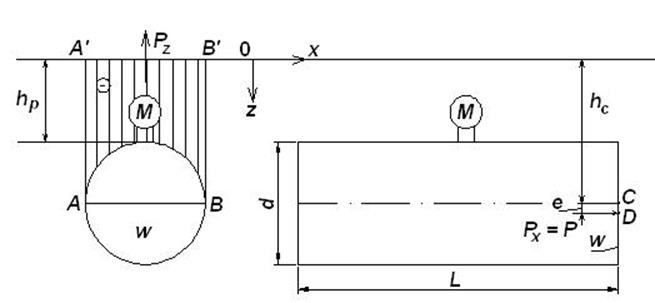
Рис. 4
Линия действия ![]() находится ниже центра тяжести площади
находится ниже центра тяжести площади![]() на величину эксцентриситета e
на величину эксцентриситета e
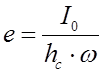
I0 – центральный момент инерции плоской фигуры ω относительно горизонтальной оси.
Для плоской фигуры, имеющей форму круга диаметром D
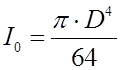
Вертикальная сила ![]() , действующая на верхнюю половину резервуара, определяется по формуле
, действующая на верхнюю половину резервуара, определяется по формуле
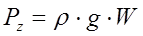
где ![]() – объем тела давления, м3.
– объем тела давления, м3.
Телом давления называется объем, ограниченный сверху пьезометрической плоскостью, снизу – цилиндрической поверхностью, с боков – вертикальными проектирующими плоскими поверхностями АА׳ и ВВ׳.
Pz будет иметь знак «+», если тело давления и жидкость примыкают к цилиндрической поверхности с одной стороны; в противном случае Pz имеет знак «-».
Чтобы получить объем тела давления W, нужно площадь поперечного сечения тела давления F (на рис. 4 заштрихована) умножить на L.
Задача № 3
Вертикальный цилиндрический резервуар высотой Н и диаметром D закрывается полусферической крышкой, сообщающейся с атмосферой через трубу с внутренним диаметром d (рис. 5). Резервуар заполнен мазутом, плотность которого ![]() = 900 кг/м3 .
= 900 кг/м3 .
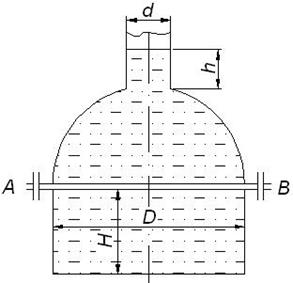
Рис. 5.
Требуется определить:
1. Высоту поднятия мазута h при повышении температуры на t0C
2. Силу, отрывающую крышку резервуара при подъеме мазута на высоту h за счет его разогрева.
Коэффициент температурного расширения мазута принять равным 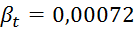 0С-1.
0С-1.
Таблица 3.
|
No вар. |
D, м |
H, м |
d, мм |
t, 0С |
No вар. |
D, м |
H, м |
d, мм |
t, 0С |
|
1 |
2,0 |
2,0 |
250 |
15 |
14 |
3,6 |
3,0 |
300 |
20 |
|
2 |
2,5 |
3,0 |
300 |
20 |
15 |
3,0 |
2,5 |
250 |
10 |
|
3 |
1,8 |
1,5 |
150 |
25 |
16 |
1,1 |
3,9 |
150 |
15 |
|
4 |
1,5 |
2,5 |
100 |
10 |
17 |
3,2 |
3,5 |
350 |
10 |
|
5 |
2,2 |
2,2 |
125 |
15 |
18 |
1,2 |
4,0 |
200 |
25 |
|
6 |
1,6 |
2,6 |
75 |
20 |
19 |
3,4 |
2,8 |
250 |
210 |
|
7 |
2,4 |
3,2 |
350 |
25 |
20 |
4,6 |
2,5 |
350 |
10 |
|
8 |
1,7 |
2,8 |
250 |
15 |
21 |
2,6 |
3,0 |
300 |
20 |
|
9 |
2,3 |
3,1 |
200 |
10 |
22 |
4,0 |
1,8 |
210 |
15 |
|
10 |
1,3 |
1,2 |
100 |
25 |
23 |
3,5 |
2,1 |
150 |
20 |
|
11 |
1,0 |
4,0 |
250 |
20 |
24 |
2,8 |
2,6 |
200 |
25 |
|
12 |
1,25 |
3,8 |
200 |
10 |
25 |
1,8 |
3,2 |
150 |
22 |
|
13 |
1,5 |
3,5 |
220 |
15 |
Указания к решению задачи 3.
Вначале необходимо определить объем резервуара W, состоящий из цилиндрической и полусферической частей. Это будет первоначальный объем мазута. Затем, используя формулу для коэффициента температурного расширения βt, найти приращение этого объема за счет его увеличения при нагревании на t0С:
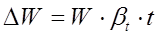
Поделив найденное приращение объема ΔW на площадь поперечного сечения трубы, получим искомую высоту поднятия мазута h.
Для нахождения усилия, отрывающего крышку резервуара от плоскости разъема АВ, необходимо найти объем тела давления Wт. д. (объем, ограниченный пьезометрической плоскостью, проведенной по свободной поверхности мазута в трубе; полусферической крышкой и вертикальной проектирующей поверхностью, построенной на контуре разъема АВ). Этот объем будет состоять из объема цилиндра диаметром D и высотой (D/2+h), из которого следует вычесть объем полусферы диаметром D и объем малого цилиндра диаметром d и высотой h.
Искомое усилие
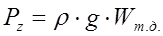
Задача № 4
У тепловоза в течение времени t равномерно изменяется скорость от ![]() до
до ![]() , в результате чего изменяется форма свободной поверхности жидкости в прицепленной к нему цистерне. Цистерна заполнена наполовину жидкостью плотностью
, в результате чего изменяется форма свободной поверхности жидкости в прицепленной к нему цистерне. Цистерна заполнена наполовину жидкостью плотностью ![]() . Диаметр цистерны D, длина L.
. Диаметр цистерны D, длина L.
Требуется:
1. Получить уравнение свободной поверхности жидкости в цистерне.
2. Насколько повысится или понизится уровень жидкости у передней стенки (по ходу движения цистерны).
3. Определить величину избыточного гидростатического давления в точке, указанной в каждом варианте задания (см. рис. 6) на поверхности жидкости в резервуаре давление равно атмосферному pа.
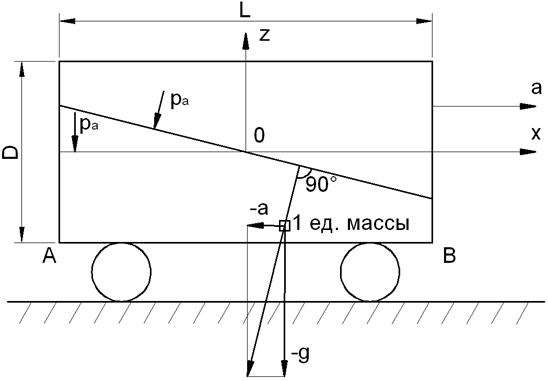
Рис. 6
Таблица 4
|
№ вар. |
|
|
t |
|
L |
D |
Название точки |
|
— |
км/ч |
км/ч |
с |
кг/м3 |
м |
м |
— |
|
1 |
5 |
20 |
7 |
1000 |
8,7 |
2,3 |
А |
|
2 |
20 |
5 |
6 |
890 |
14,7 |
3,0 |
В |
|
3 |
40 |
30 |
4 |
650 |
9,4 |
2,0 |
А |
|
4 |
45 |
30 |
5 |
900 |
10 |
2,8 |
В |
|
5 |
50 |
30 |
5 |
850 |
14,7 |
3,0 |
А |
|
6 |
70 |
36 |
10 |
830 |
9,6 |
2,6 |
В |
|
7 |
20 |
10 |
5,5 |
800 |
6,7 |
2,2 |
А |
|
8 |
10 |
30 |
6 |
1000 |
14,0 |
3,0 |
В |
|
9 |
5 |
25 |
10 |
1100 |
6,8 |
2,0 |
А |
|
10 |
10 |
40 |
5 |
790 |
12 |
2,5 |
В |
|
11 |
4 |
18 |
6 |
1000 |
8,7 |
2,1 |
А |
|
12 |
18 |
4 |
5 |
890 |
14,7 |
3,1 |
В |
|
13 |
36 |
26 |
4 |
950 |
9,4 |
2,2 |
А |
|
14 |
42 |
27 |
5 |
900 |
10 |
2,7 |
В |
|
15 |
48 |
28 |
5 |
850 |
14,7 |
2,9 |
А |
|
16 |
22 |
10 |
6 |
830 |
9,6 |
2,5 |
В |
|
17 |
8 |
28 |
6 |
800 |
6,7 |
2,0 |
А |
|
18 |
7 |
27 |
10 |
1000 |
14,0 |
2,6 |
В |
|
19 |
12 |
42 |
5 |
1100 |
6,8 |
2,5 |
А |
|
20 |
42 |
32 |
4 |
790 |
12,0 |
2,7 |
В |
|
21 |
46 |
32 |
5 |
1000 |
9,4 |
3,2 |
А |
|
22 |
52 |
32 |
5 |
890 |
10,0 |
3,0 |
В |
|
23 |
68 |
34 |
10 |
950 |
14,7 |
3,1 |
А |
|
24 |
22 |
12 |
5,5 |
900 |
9,6 |
2,6 |
В |
|
25 |
12 |
32 |
6,0 |
850 |
6,7 |
2,8 |
А |
Указанию к решению задачи 4.
1. Для получения уравнения свободной поверхности жидкости нужно воспользоваться общим, объединенным уравнением равновесия жидкости, выраженным в дифференциальной форме:
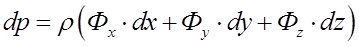
и применить его к жидкости, находящейся под действием сил тяжести и сил инерции.
В этом случае в формуле гидростатическое давление на свободной поверхности жидкости равно pа = const; ![]() ,
, ![]() и
и ![]() – проекции на соответствующие оси координат объемных сил, действующих на единицу массы жидкости. При этом Фx = — a; Фy = 0; Фz = — g. Горизонтальное ускорение a, м/с2, определяется по формуле
– проекции на соответствующие оси координат объемных сил, действующих на единицу массы жидкости. При этом Фx = — a; Фy = 0; Фz = — g. Горизонтальное ускорение a, м/с2, определяется по формуле
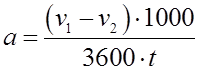
После этого решается полученное дифференциальное уравнение и находится уравнение свободной поверхности.
2. Для получения ответа на второй вопрос нужно в полученное уравнение свободной поверхности подставить координаты указанной в каждом варианте точки.
3. Для определения величины избыточного гидростатического давления в заданной точке снова обращаемся к дифференциальному уравнению и решаем его относительно p
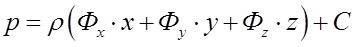
где Фx = — a; Фy = 0; Фz = — g.
Величину "С" определяем, записав уравнение для начала координат. Подставляя в полученное окончательное выражение для p координаты указанной в задании точки, получим величину избыточного гидростатического давления в ней.
Задача № 5
Вода в количестве Q л/с забирается насосом из берегового колодца А, который соединен с водоемом Б самотечной трубой длиной ![]() и диаметром dc (рис. 7). Длина всасывающей трубы lвс = l1 + l2, ее диаметр dвс. Средняя высота выступов на внутренней поверхности стенок труб (шероховатость) Δс=0,5 мм; Δвс= 0,25 мм. Коэффициент местного сопротивления сетки самотечной трубы ζс=5; коэффициент местного сопротивления на выход из самотечной трубы ζвых=1; сетки с обратным клапаном всасывающей трубы ζкл=3, колена всасывающей трубы ζк=0,3.допускаемый вакуум в трубопроводе перед входом в насос hвак=6,8 м.
и диаметром dc (рис. 7). Длина всасывающей трубы lвс = l1 + l2, ее диаметр dвс. Средняя высота выступов на внутренней поверхности стенок труб (шероховатость) Δс=0,5 мм; Δвс= 0,25 мм. Коэффициент местного сопротивления сетки самотечной трубы ζс=5; коэффициент местного сопротивления на выход из самотечной трубы ζвых=1; сетки с обратным клапаном всасывающей трубы ζкл=3, колена всасывающей трубы ζк=0,3.допускаемый вакуум в трубопроводе перед входом в насос hвак=6,8 м.
Определить максимально допустимую высоту расположения оси насоса над уровнем воды в колодце hн, разность уровней воды в водоеме и в колодце z.
Построить напорную и пьезометрическую линии для самотечной трубы.
Примечание: 1) скоростями движения воды в сечениях на свободной поверхности воды в водоеме и в колодце следует пренебречь. 2) t = 10оС.
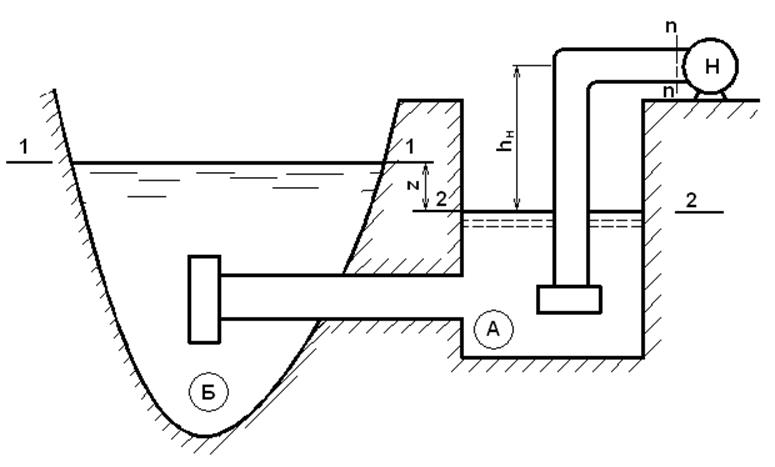
Рис. 7.
Таблица 5
|
№ Варианта |
Q, л/с |
м |
мм |
м |
мм |
|
1 |
4,0 |
40 |
75 |
8,5 |
50 |
|
2 |
6,0 |
65 |
100 |
9,0 |
75 |
|
3 |
10,0 |
50 |
125 |
10,0 |
100 |
|
4 |
7,5 |
75 |
100 |
9,2 |
75 |
|
5 |
8,5 |
60 |
150 |
9,5 |
100 |
|
6 |
10,0 |
55 |
175 |
10,5 |
125 |
|
7 |
9,5 |
58 |
125 |
10,0 |
100 |
|
8 |
6,5 |
62 |
100 |
8,8 |
75 |
|
9 |
9,0 |
55 |
100 |
9,8 |
125 |
|
10 |
7,0 |
64 |
100 |
9,3 |
75 |
|
11 |
5,0 |
45 |
75 |
8,5 |
60 |
|
12 |
6,5 |
50 |
100 |
9,0 |
75 |
|
131 |
9,5 |
55 |
125 |
9,2 |
100 |
|
4 |
8,5 |
58 |
125 |
10,0 |
75 |
|
15 |
6,0 |
60 |
100 |
9,5 |
75 |
|
16 |
4,0 |
50 |
75 |
10,5 |
50 |
|
17 |
5,5 |
60 |
75 |
10,0 |
60 |
|
18 |
10,0 |
55 |
150 |
12,0 |
125 |
|
19 |
9,5 |
50 |
125 |
11,0 |
100 |
|
20 |
6,5 |
60 |
100 |
9,3 |
75 |
|
21 |
9,0 |
50 |
125 |
9,5 |
100 |
|
22 |
7,0 |
62 |
100 |
10,0 |
75 |
|
23 |
5,0 |
44 |
75 |
9,8 |
75 |
|
24 |
6,5 |
55 |
100 |
8,5 |
100 |
|
25 |
5,5 |
50 |
75 |
10,5 |
50 |
Указание к решению задачи 5
Чтобы определить превышение уровня в береговом колодце А над уровнем в водоеме Б следует составить уравнение Бернулли для двух сечений потока: сечения 1 – 1 на поверхности воды в водоёме и сечения 2 – 2 на поверхности воды в береговом колодце. Плоскость сравнения провести по уровню воды в береговом колодце, т. е. по сечению 2 – 2;
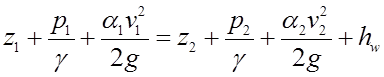
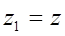 ;
; 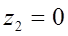 ;
; 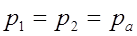
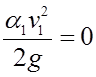 ;
; 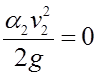 .
.
т. к. по условию задачи 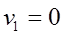 и
и 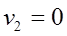 .
.
После проведенного анализа членов уравнения, получим следующее уравнение
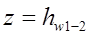
где 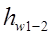 – потери напора при движении воды по самотечной трубе.
– потери напора при движении воды по самотечной трубе.
Так как самотечная и всасывающая труба рассматриваются как короткий трубопровод, то при их расчете учитываются оба вида потерь напора: местные и по длине.
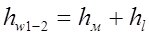
где ![]() – потери напора в местных сопротивлениях, которые вычисляются по формуле Вейсбаха.
– потери напора в местных сопротивлениях, которые вычисляются по формуле Вейсбаха.
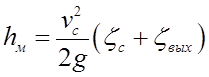
Потери напора по длине за счет трения жидкости о стенки трубы определяются по формуле Вейсбаха-Дарси
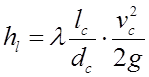
где λ — коэффициент гидравлического трения;
lc — длина самотечного трубопровода;
dc — диаметр самотечного трубопровода.
Коэффициент λ может быть определен по формуле А. Д. Альтшуля.
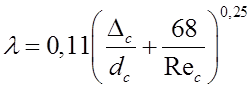
где ![]() — шероховатость самотечной трубы;
— шероховатость самотечной трубы;
Rec — число Рейнольдса на участке самотечной трубы
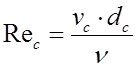
где ![]() – кинематический коэффициент вязкости (для t = 10 0С,
– кинематический коэффициент вязкости (для t = 10 0С, ![]() = 0,0131 см2/с).
= 0,0131 см2/с).
Подставив значения ![]() и
и ![]() в расчетные зависимости и определим разность уровней воды в водоеме и в береговом колодце.
в расчетные зависимости и определим разность уровней воды в водоеме и в береговом колодце.
Для определения высоты расположения насоса над уровнем воды в береговом колодце следует составить уравнение Бернулли для сечений 2 – 2 на поверхности воды в береговом колодце и n – n перед насосом. Плоскость сравнения провести по уровню воды в береговом колодце, т. е. по сечению 2 – 2.
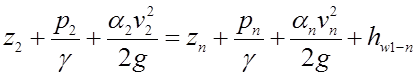
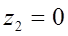 ;
; 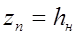 ;
; 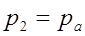 ;
; 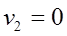 – по условию задачи;
– по условию задачи; 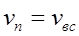 — скорость движения воды во всасывающей трубе;
— скорость движения воды во всасывающей трубе; ![]() принимается равным 1,0.
принимается равным 1,0.
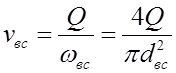
Подставим в уравнение все известные величины
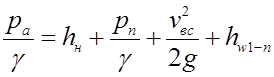
Переписав в левую часть ![]() , мы получим величину вакуума в сечении n – n
, мы получим величину вакуума в сечении n – n
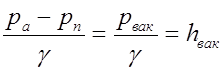
Таким образом, окончательно расчетное выражение будет иметь вид:
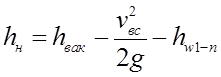
где
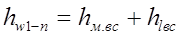
потери напора во всасывающей трубе.
Местные потери напора во всасывающей трубе
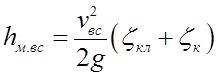
Потери напора по длине на всасывающей трубе
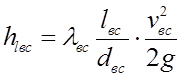
![]() определяется по формуле Альтшуля.
определяется по формуле Альтшуля.
Подставив в выражение значения вакуума, скоростной высоты ![]() и потери напора во всасывающей трубе, получим величину hн.
и потери напора во всасывающей трубе, получим величину hн.
Далее необходимо построить напорную линию, которая представляет собой график распределения напора по длине.
В пределах водоема напорная линия совпадает с линией поверхности воды, т. к. скоростью в пределах водоема пренебрегаем.
При входе в самотечную трубу напор скачкообразно уменьшается на величину потери напора на сетке самотечной трубы 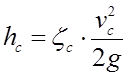 .
.
В плоскости входного сечения в самотечную трубу откладываем эту величину вниз от уровня воды в водоеме. Далее происходит потеря по длине, которая в конце участка самотечной трубы достигает величины
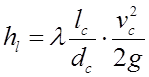
Для построения напорной линии с учетом потери напора по длине поступаем следующим образом. Из конца вертикального отрезка hc проводим горизонтальную линию и в конце участка самотечной трубы откладываем от нее вниз величину hl и соединяем наклонной линией концы отрезков hc и hl. В выходном сечении самотечного трубопровода происходит местная потеря на выходе, поэтому из конца наклонной линии откладываем величину 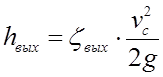 .
.
Пьезометрическая линия P – P будет располагаться ниже напорной Н – H на величину скоростной высоты ![]() .
.
Задача № 6
Расчет разветвленного тупикового газопровода при малом перепаде давления
Студентам предлагается рассчитать вентиляционный воздуховод, схема которого показана на рис.8. Вентилятор подает воздух в два помещения по каналам 3-4 и 3-5. На выходе из каналов установлены поворотные заслонки для регулировки расхода воздуха. Задачей гидравлического расчета является определение необходимого избыточного давления на входе в систему для подбора вентилятора при условии обеспечения заданных расходов воздуха на выходе из каналов 3-4 и 3-5.
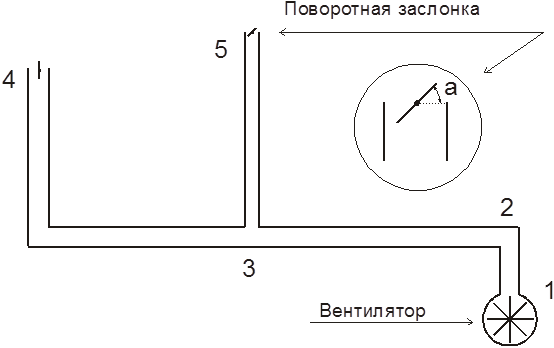
Рис. 8
Основой расчетов газопроводов, так же как и для расчетов напорных трубопроводов для капельных жидкостей, является уравнение Бернулли. Но для газопроводов используется другая форма уравнения. Для расчета потоков капельных жидкостей в гидравлике принято оперировать понятием напора жидкости, который измеряется в метрах. По ряду причин напор не годится для оценки потоков газов. Например, потенциальный напор капельной жидкости определяется уровнем ее свободной поверхности, а газы не образуют свободной поверхности.
Уравнение Бернулли легко преобразуется таким образом, что все его члены измеряются не в метрах, а в паскалях, то есть представляют собой давления.
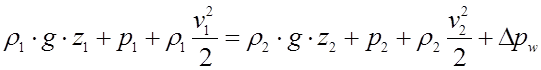
Уравнение (1) используется для расчета газопроводов. В нем ρ – плотность газа, g – ускорение свободного падения, z – геометрическая высота, p – давление газа, v – средняя скорость потока газа, ![]() — динамическое давление, Δpw – потери давления, которые, так же как потери напора, отражают затраты энергии на преодоление сопротивлений движению жидкости.
— динамическое давление, Δpw – потери давления, которые, так же как потери напора, отражают затраты энергии на преодоление сопротивлений движению жидкости.
Методика использования уравнения Бернулли определяется величиной перепада давления в газопроводе. Относительным перепадом давления называется отношение потери давления Δp к средней величине давления ![]() (см. рис. 9).
(см. рис. 9).

![]() газопровод
газопровод
 |
Рис. 9
Перепадом давления называется разность давлений в начале и в конце трубопровода 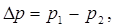 а средняя величина давления вычисляется как их полусумма
а средняя величина давления вычисляется как их полусумма 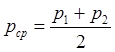 .
.
Различают газопроводы с малыми перепадами давления ![]()
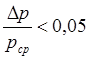 и с большими перепадами давления
и с большими перепадами давления 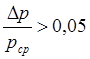 .
.
Плотность газов, в отличие от плотности капельных жидкостей, сильно зависит от давления. Согласно уравнению Бернулли, при движении газа по трубопроводу происходят потери давления Dp, а, следовательно, изменяется плотность газа r. Поэтому при гидравлическом расчете газопроводов возникает задача учета изменений плотности газа по длине потока. Но если плотность изменяется незначительно, ее изменениями можно пренебречь без существенного ущерба для точности расчета.
При расчете газопроводов с малым перепадом давления плотность газа считается постоянной величиной. При расчете газопроводов с большим перепадом давления необходимо учитывать изменения плотности газа по длине потока, что существенно усложняет гидравлический расчет. Вентиляционные трубопроводы относятся к газопроводам с малым перепадом давления.
В трубопроводах вентиляционных систем возникают значительные местные сопротивления, которые необходимо учитывать в гидравлических расчетах. Поэтому вентиляционные газопроводы рассчитываются как короткие трубопроводы.
Методика расчета в общих чертах заключается в следующем.
1. Задаются необходимые для вентиляции помещений расходы воздуха Q по соответствующим техническим нормативам.
2. Назначаются длины трубопроводов L в соответствии с размерами
вентилируемого объекта.
3. Выбирается материал трубопроводов и соответствующая величина
эквивалентной шероховатости Δ.
4. Задаются форма и размеры поперечного сечения трубопроводов, конструкция разветвлений, соединений труб разного диаметра,
отводов и регулирующих устройств.
5. На основе перечисленных исходных данных вычисляется потеря
давления в системе.
В воздушных вентиляционных системах величины гравитационного давления ρgz в уравнении пренебрежимо малы по сравнению с другими членами уравнения. Поэтому для расчета используется упрощенное уравнение Бернулли в форме
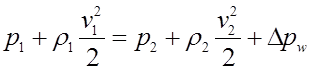
Суммарная потеря давления Δpw является суммой потерь по длине и местных потерь Δpw = ΔpL + Δpм . Потери по длине вычисляются по формуле
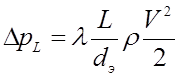
где l — коэффициент гидравлического трения, L – длина рассматриваемого участка газопровода, dэ = 4R — эквивалентный диаметр живого сечения потока газа, R – гидравлический радиус живого сечения.
Местные потери вычисляются по формуле
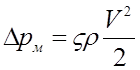
в которой z — коэффициент местного сопротивления
Величины dэ для трубопроводов с различной формой поперечного сечения даны в таблице 6.
Таблица 6
|
dэ |
Форма сечения | ||||
|
|||||
|
|
||||
|
Рассмотрим расчет газопровода с малым перепадом давления на примере разветвленной тупиковой вентиляционной системы, изображенной на рисунке 8.
1. Заданы расходы воздуха в конце участков:
3-4 – 0,7 м3/с,
3-5 – 0,4 м3/с.
2. Длины участков:
1-2 – 4м,
2-3 – 25м,
3-4 – 30 м,
3-5 – 10 м.
3. Поскольку трубопровод разветвленный, выбираем и рассчитываем
магистраль по признаку максимальной длины трубопровода 1-2-3-4.
Участок 3-5 будем рассматривать как ответвление магистрали. Расчет удобно вести в табличной форме. Для этого создаем таблицу 7.
4. Трубопроводы из шлакогипсовых плит с шероховатостью поверхности D = 1 мм.
5. Трубопроводы прямоугольного поперечного сечения с размерами, указанными в таблице 7.
6. Максимальная допускаемая скорость потока воздуха из условия допускаемого уровня шума Vдоп = 12 м/с.
7. Коэффициенты местных сопротивлений:
отводы (колена) на участках 2-3 и 3-4 zk = 1,2,
поворотные заслонки на выходе участков 3-4 и 3-5, полностью открытые zз = 1,6 ,
прямой проход через тройник на магистрали zтп = 0,13,
отвод через тройник в ответвление zто = 2,7.
8. Расходы на участках 1-2 и 2-3 равны сумме расходов на участках 3-4 и 3-5:
Q1-2 = Q2-3 = 0,7 + 0,4 = 1,1 м3/с.
9. Вычисляем скорости на участках по формуле V = Q/w. Если вычисленные скорости больше допускаемой, сечения трубопроводов надо увеличить.
10.Вычисляем динамическое давление по формуле 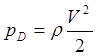 .
.
При малом перепаде давления плотность можно считать постоянной.
Принимаем ее равной плотности воздуха в стандартных условиях (200С; 101,325 кПа) ![]() = 1,2 кг/м3.
= 1,2 кг/м3.
11.Вычисляем коэффициент гидравлического трения по формуле Альтшуля
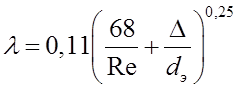
Число Рейнольдса вычисляем по формуле
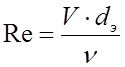
Эквивалентный диаметр dэ определяем, пользуясь таблицей 6.
Кинематический коэффициент вязкости воздуха в стандартных условиях можно принимать равным ν = 15,06 . 10-6 м2/с.
12.Вычисляем потери давления по длине по формуле.
13.Записываем в таблицу величины коэффициентов местного сопротивления и вычисляем суммарные коэффициенты сопротивления участков.
14.Вычисляем местные потери давления на участках по формуле, суммарные потери на участках ![]() и суммарную потерю давления в магистрали.
и суммарную потерю давления в магистрали.
На основе величины суммарной потери давления в магистрали заключаем, что для обеспечения заданных расходов воздуха необходим вентилятор, создающий давление на входе в газопровод около 300 Па.
Выполненные расчеты показали, что в ответвлении 3-5 при заданном расходе Q3-5 = 0,4 м3/с потеря давления составит 82,86 Па. На участке 3-4 магистрали расчетная потеря давления 113,03 Па. Это означает, что гидравлическое сопротивление в ответвлении меньше, чем в магистрали. При этом расход в ответвлении будет больше, а в магистрали меньше заданных величин. Для обеспечения заданных расходов необходимо уравнять потери давления в ответвлении и в магистрали. Для этого можно увеличить потери давления в ответвлении, частично закрывая поворотную заслонку на выходе участка 3-5. Определим необходимый угол открытия заслонки α°.
Потерю давления в ответвлении надо увеличить на Dp = 113,03 – 82,86 = 30,17 Па (см. таблицу 7). Для этого надо увеличить коэффициент местного сопротивления поворотной заслонки на выходе участка 3-5 на величину Dzз, которую можно вычислить по формуле (4)
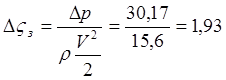
Суммарный коэффициент местного сопротивления заслонки должен быть равным
zз + Dzз = 1,6 + 1,93 = 3,53
Необходимый для этого угол открытия заслонки a0 » 580 находим, пользуясь таблицей 8.
Таблица 7
|
Параметр |
Обозначение |
Ед. изм. |
Магистраль |
Ответвление |
||
|
3-4 |
2-3 |
1-2 |
3-5 |
|||
|
Заданный расход в конце участка |
Qз |
м3/с |
0,7 |
— |
— |
0,4 |
|
Длина участка |
L |
м |
30 |
25 |
4 |
10 |
|
Эквивалентная шероховатость |
Δ |
мм |
1 |
|||
|
Размеры сечений |
a . b |
мм |
280 . 420 |
280 . 280 |
||
|
Допускаемая скорость |
Vдоп |
м/с |
12 |
|||
|
Расход на участках |
Q |
м3/с |
0,7 |
1,1 |
1,1 |
0,4 |
|
Скорость на участках |
V |
м/с |
5,95 |
9,35 |
9,35 |
5,1 |
|
Динамическое давление |
pD |
Па |
21,24 |
52,45 |
52,45 |
15,6 |
|
Эквивалентный диаметр |
dэ |
мм |
336 |
280 |
||
|
Число Рейнольдса |
Re |
— |
132700 |
208600 |
94800 |
|
|
Коэффициент гидравлического трения |
λ |
— |
0,027 |
0,026 |
0,028 |
|
|
Потери давления по длине |
ΔpL |
Па |
50,74 |
102,99 |
16,48 |
15,70 |
|
Коэффициенты местных сопротивлений |
ζтп |
— |
0,13 |
— |
— |
— |
|
ζк |
— |
1,2 |
1,2 |
— |
— |
|
|
ζтo |
— |
— |
— |
— |
2,7 |
|
|
ζз |
— |
1,6 |
— |
— |
1,6 |
|
|
Σζ |
— |
2,93 |
1,2 |
— |
4,3 |
|
|
Местные потери давления |
ΔpM |
Па |
62,29 |
63,00 |
0 |
67,16 |
|
Суммарные потери на участках |
ΔpW |
Па |
113,03 |
165,99 |
16,48 |
82,86 |
|
Суммарная потеря в магистрали |
ΔpW |
Па |
295,50 |
|||
Таблица 8
|
a0 |
90 |
85 |
80 |
75 |
70 |
65 |
60 |
55 |
50 |
45 |
40 |
35 |
30 |
25 |
20 |
15 |
|
z |
1,6 |
1,8 |
2,0 |
2,3 |
2,6 |
2,9 |
3,3 |
3,8 |
4,4 |
5,2 |
6,1 |
7,4 |
9,2 |
12,3 |
18 |
31 |
Таблица 9
Варианты заданий
|
№ |
Материал |
D, мм |
Сечения, м |
Расходы, м3/с |
Длины, м |
|||||
|
1-2-3-4 |
3-5 |
3-4 |
3-5 |
1-2 |
2-3 |
3-4 |
3-5 |
|||
|
1 |
Лист. сталь |
0,1 |
0,2* |
0,1 |
0,25 |
0,08 |
4 |
18 |
28 |
22 |
|
2 |
0,25* |
0,15 |
0,4 |
0,15 |
4 |
18 |
28 |
22 |
||
|
3 |
Фанера |
0,2 |
0,2 . 0,15 |
0,15 . 0,15 |
0,2 |
0,15 |
4 |
17 |
27 |
21 |
|
4 |
0,25 . 0,2 |
0,2 . 0,15 |
0,4 |
0,15 |
4 |
16 |
25 |
20 |
||
|
5 |
Шлакогипс |
1,0 |
0,28 . 0,28 |
0,28 . 0,14 |
0,6 |
0,3 |
4 |
15 |
23 |
19 |
|
6 |
0,42 . 0,28 |
0,28 . 0,28 |
1,0 |
0,4 |
4 |
15 |
23 |
19 |
||
|
7 |
Шлакобетон |
1,5 |
0,2 . 0,15 |
0,15 . 0,1 |
0,23 |
0,12 |
4 |
14 |
22 |
18 |
|
8 |
0,2 . 0,2 |
0,15 . 0,15 |
0,3 |
0,15 |
4 |
13 |
21 |
17 |
||
|
9 |
Кирпичная кладка |
5 |
0,27 . 0,14 |
0,14 . 0,14 |
0,25 |
0,15 |
4 |
12 |
19 |
15 |
|
10 |
0,4 . 0,27 |
0,27 . 0,14 |
0,8 |
0,4 |
4 |
12 |
19 |
15 |
||
|
№ |
Материал |
D, мм |
Сечения, м |
Расходы, м3/с |
Длины, м |
|||||
|
1-2-3-5 |
3-4 |
3-4 |
3-5 |
1-2 |
2-3 |
3-4 |
3-5 |
|||
|
11 |
Листовая сталь |
0,1 |
0,2* |
0,1* |
0,08 |
0,25 |
4 |
10 |
27 |
36 |
|
12 |
0,25* |
0,15* |
0,15 |
0,40 |
4 |
10 |
26 |
34 |
||
|
13 |
0,3* |
0,2* |
0,20 |
0,60 |
4 |
10 |
25 |
32 |
||
|
14 |
Фанера |
0,2 |
0,20∙0,15 |
0,15∙0,15 |
0,15 |
0,20 |
4 |
10 |
24 |
30 |
|
15 |
0,25∙0,20 |
0,20∙0,15 |
0,15 |
0,40 |
4 |
10 |
23 |
28 |
||
|
16 |
0,30∙0,25 |
0,20∙0,15 |
0,30 |
0,60 |
4 |
10 |
22 |
26 |
||
|
17 |
Шлакогипс |
1,0 |
0,28∙0,28 |
0,28∙0,14 |
0,30 |
0,60 |
4 |
10 |
21 |
24 |
|
18 |
0,42∙0,28 |
0,28∙0,28 |
0,40 |
1,00 |
4 |
10 |
20 |
23 |
||
|
19 |
0,42∙0,42 |
0,42∙0,28 |
0,75 |
1,25 |
4 |
10 |
19 |
22 |
||
|
20 |
Шлакобетон |
1,5 |
0,20∙0,15 |
0,15∙0,10 |
0,12 |
0,23 |
4 |
10 |
18 |
21 |
|
21 |
0,20∙0,20 |
0,15∙0,15 |
0,15 |
0,30 |
4 |
10 |
17 |
20 |
||
|
22 |
0,30∙0,20 |
0,20∙0,15 |
0,25 |
0,45 |
4 |
10 |
16 |
19 |
||
|
23 |
Кирпичная кладка |
0,27∙0,14 |
0,14∙0,14 |
0,15 |
0,25 |
4 |
10 |
15 |
18 |
|
|
24 |
0,40∙0,27 |
0,27∙0,14 |
0,40 |
0,80 |
4 |
10 |
14 |
17 |
||
|
25 |
0,40∙0,40 |
0,40∙0,27 |
0,90 |
1,00 |
4 |
10 |
13 |
16 |
*) Диаметр трубопровода круглого поперечного сечения, в других вариантах трубопроводы прямоугольного сечения а·в, или квадратного а∙а.
Задача 7
Гидравлический расчет вытяжной дымовой трубы.
Функцией вытяжной трубы является создание потока воздуха из здания через топку котла и т. п. в атмосферу. Устойчивый поток воздуха в трубе возникает под действием двух естественных побудительных факторов:
— при обдувании ветром оголовка трубы в выходном сечении возникает локальное понижение давления, при этом давление внутри здания может оказаться достаточным для создания потока воздуха из здания в атмосферу в условиях изотермического процесса, т. е. когда котел не топится;
— если котел топится и труба заполнена (дымом), температура которого выше, чем в атмосфере (а плотность соответственно меньше), то согласно закону Архимеда теплый воздух «вытесняется» вверх.
Так как в процессе розжига котла дым также не должен поступать внутрь помещения, то расчет производится на 2 случая:
1. Котел не топится, но задвижка на трубе открыта (момент растопки котла):
2. Котел топится.
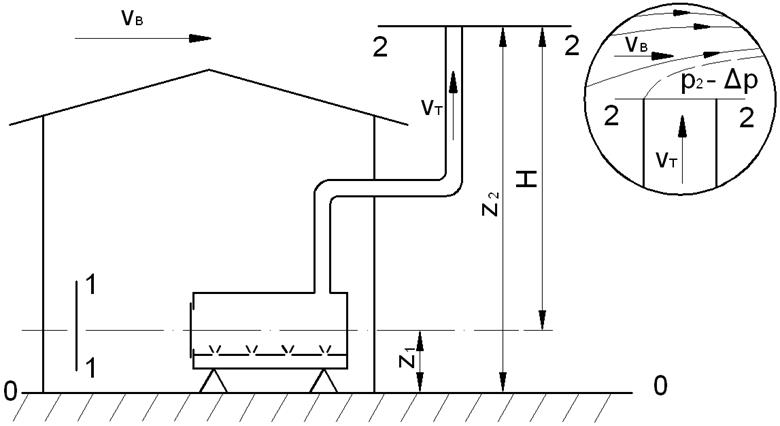
Рис. 10
Дано: труба металлическая диаметром dт, шероховатость стенок трубы Δ, коэффициент местного сопротивления одного поворота ζп. температура воздуха внутри и вне помещения в момент розжига котла tв, °С. Температура нагретого воздуха на входе в трубу при работе котла tт, °С.
Оголовок трубы снабжен колпаком. Среднемноголетнее значение скорости ветра vв (м/с). Общая длина трубы lт, м. Заданы также возвышения сечений 1-1 и 2-2 над плоскостью сравнения (Z1 и Z2).
Требуется: определить расход воздуха (при работе котла-дыма) для двух случаев:
1. Котел не топится, но задвижка на трубе открыта.
2. Котел топится.
Таблица 10
|
№ Вар. |
|
|
|
|
|
|
|
|
|
|
— |
мм |
мм |
— |
0С |
0С |
м/с |
м |
м |
м |
|
1 |
150 |
0,8 |
0,8 |
0 |
340 |
3,5 |
12 |
1,5 |
9,1 |
|
2 |
200 |
1,0 |
0,8 |
0 |
320 |
2,8 |
15 |
1,8 |
12,0 |
|
3 |
250 |
1,0 |
0,8 |
0 |
300 |
2,5 |
17 |
2,0 |
12,5 |
|
4 |
150 |
1,0 |
0,9 |
10 |
360 |
3,0 |
13 |
1,4 |
10,2 |
|
5 |
200 |
0,8 |
0,9 |
10 |
380 |
4,0 |
14 |
1,7 |
8,5 |
|
6 |
250 |
1,5 |
0,9 |
10 |
400 |
4,5 |
16 |
2,1 |
9,5 |
|
7 |
150 |
1,5 |
1,0 |
20 |
410 |
5,0 |
11 |
1,5 |
8,0 |
|
8 |
200 |
0,8 |
1,0 |
20 |
420 |
2,6 |
13 |
1,7 |
8,5 |
|
9 |
250 |
1,5 |
1,0 |
20 |
430 |
3,0 |
16 |
2,0 |
12,0 |
|
10 |
150 |
0,9 |
1,1 |
5 |
440 |
4,0 |
12 |
1,4 |
8,1 |
|
11 |
200 |
1,2 |
1,1 |
5 |
450 |
5,0 |
13 |
1,6 |
9,0 |
|
12 |
250 |
1,2 |
1,1 |
5 |
460 |
3,2 |
17 |
2,1 |
13,0 |
|
13 |
150 |
1,0 |
1,2 |
15 |
330 |
4,1 |
13 |
1,3 |
10,2 |
|
14 |
200 |
1,2 |
1,2 |
15 |
370 |
5,1 |
14 |
1,5 |
10,5 |
|
15 |
250 |
0,8 |
1,2 |
15 |
390 |
3,6 |
15 |
1,7 |
9,7 |
|
16 |
150 |
1,1 |
0,85 |
0 |
320 |
4,2 |
14 |
1,3 |
9,1 |
|
17 |
200 |
0,9 |
0,85 |
0 |
340 |
5,2 |
15 |
1,5 |
10,1 |
|
18 |
250 |
0,9 |
0,85 |
0 |
360 |
3,0 |
16 |
1,6 |
11,5 |
|
19 |
150 |
1,4 |
0,95 |
10 |
380 |
4,0 |
12 |
1,4 |
8,3 |
|
20 |
200 |
1,4 |
0,95 |
10 |
400 |
5,0 |
14 |
1,5 |
9,3 |
|
21 |
250 |
1,4 |
0,95 |
10 |
410 |
3,1 |
16 |
1,4 |
10,3 |
|
22 |
150 |
1,3 |
1,15 |
15 |
420 |
4,1 |
13 |
1,5 |
9,5 |
|
23 |
200 |
1,3 |
1,15 |
15 |
430 |
5,1 |
15 |
1,4 |
10,5 |
|
24 |
250 |
1,3 |
1,15 |
15 |
440 |
2,6 |
17 |
1,5 |
11,5 |
|
25 |
150 |
0,9 |
1,3 |
0 |
370 |
5,5 |
12 |
1,3 |
8,7 |
![]() — температура воздуха внутри и вне помещения, когда котел не топится.
— температура воздуха внутри и вне помещения, когда котел не топится.
![]() — температура воздуха на входе в трубу при работе котла.
— температура воздуха на входе в трубу при работе котла.
Указания к решению задачи № 7.
1й случай. Котел не топится, но задвижка на трубе открыта.
1. Запишем уравнение Бернулли для сечений 1-1 и 2-2, показанных на рис. 10, полагая, что температура воздуха, а следовательно, и его плотность ![]() в помещении и вне его одинаковы:
в помещении и вне его одинаковы:
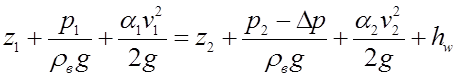
где Р1 и Р2 – атмосферное давление на высоте Z1 и Z2;
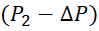 – давление в сечении 2-2;
– давление в сечении 2-2; 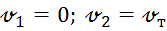 – скорость потока воздуха в трубе;
– скорость потока воздуха в трубе; 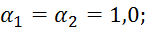
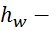 общие потери напора от сечения 1-1 до сечения 2-2.
общие потери напора от сечения 1-1 до сечения 2-2.
2. Учитывая, что напоры в сечениях 1-1 и 2-2 (при отсутствия ветра) одинаковы 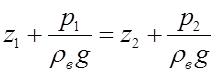 , а также сказанное выше, из получаем следующее выражение
, а также сказанное выше, из получаем следующее выражение
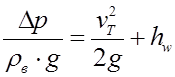
3. Локальное понижение давления ![]() относительно атмосферного давления в окрестности выходного сечения трубы определяется по зависимости:
относительно атмосферного давления в окрестности выходного сечения трубы определяется по зависимости:
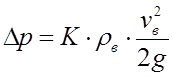
где К – коэффициент, значения которого зависят от конструкции оголовка и находятся по графику, представленному в приложении 4 (конструкция выбирается студентом самостоятельно).
4. Потери напора в трубе вычисляются по формуле:
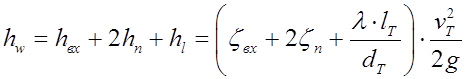
где hвх — потери напора на входе в трубу;
hп — потери напора на повороте трубы; λ — коэффициент гидравлического трения трубы; ζп — коэффициент местного сопротивления на вход в трубу, принимаемый равный 0,5.
5. В 1ом приближении коэффициент гидравлического трения ![]() определяем по формуле:
определяем по формуле:
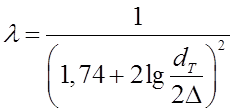
6. Определяем сумму коэффициентов местных сопротивлений
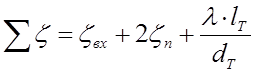
7. По графику Приложения 4 для выбранного типа оголовка определяем коэффициент “K”.
8. Подставляя в формулу вместо Δp и hw их выражения по и, получим расчетную зависимость для определения скорости движения воздуха в трубе:
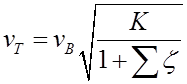
9. Используя полученное значение ![]() и данные по величине коэффициента кинематической вязкости воздуха
и данные по величине коэффициента кинематической вязкости воздуха ![]() при температуре
при температуре ![]() уточняем величину коэффициента гидравлического трения
уточняем величину коэффициента гидравлического трения ![]()
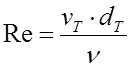
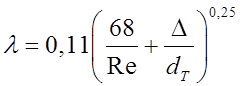
10.По формуле находим уточненное значение скорости воздуха в трубе.
11.Вычисляем расход воздуха в трубе
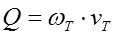
где ![]() — площадь живого сечения трубы.
— площадь живого сечения трубы.
2й расчетный случай. Котел топится.
Труба заполнена горячим воздухом (дымом), плотность которого ![]() меньше плотности атмосферного воздуха. Температура горячего воздуха tт задана.
меньше плотности атмосферного воздуха. Температура горячего воздуха tт задана.
1. Запишем уравнение Бернулли для потока воздуха в трубе, выбрав сечения 1-1 и 2-2 и плоскость сравнения 0-0, как показано на рис. 10. Так как скорость нагретого воздуха в трубе соизмерима, а зачастую и превосходит скорость ветра, то эффективность побуждающего фактора, связанного с обдуванием оголовка трубы в штатном режиме ее работы (т. е. когда котел топится) невелика и его на этой стадии не учитывают.
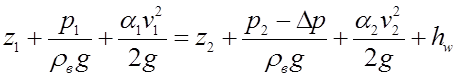
где 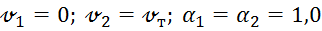 потеря напора
потеря напора
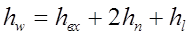
где
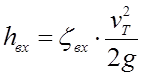 ;
; 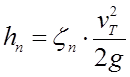 ;
; 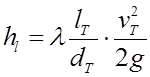 .
.
2. С учетом сказанного перепишем уравнение в следующем виде:
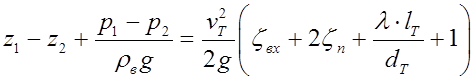
3. Определим разность давлений (p1 – p2), предполагая, что распределение давления в атмосфере и внутри здания (вне трубы) подчиняется гидростатическому закону, т. е.
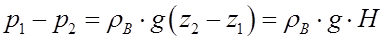
4. Подставим в вместо (p1 – p2) его выражение по, а вместо 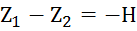 , получим следующую расчетную зависимость для вычисления
, получим следующую расчетную зависимость для вычисления ![]()
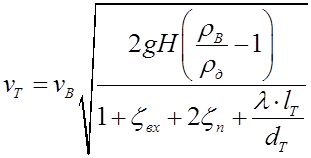
5. Так как нам неизвестна область гидравлического сопротивления трубы, то в 1ом приближении ![]() определяем по формуле
определяем по формуле
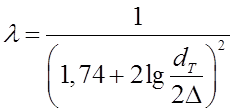
6. Плотность воздуха при температурах ![]() и
и ![]() определяем по таблице Приложения 5.
определяем по таблице Приложения 5.
7. Подставляя все заданные и найденные величины в правую часть формулы, находим ![]() .
.
8. Уточняем коэффициент гидравлического трения ![]() , для чего прежде всего используя таблицу приложения 1 устанавливаем область гидравлического сопротивления трубы. При этом
, для чего прежде всего используя таблицу приложения 1 устанавливаем область гидравлического сопротивления трубы. При этом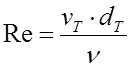 ;
; ![]() принимается по таблице приложения 1.
принимается по таблице приложения 1.
9. По формуле вычисляем уточненное значение скорости горячего воздуха (дыма) в трубе.
10.Определяем расход воздуха в трубе
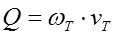
Задача № 8
Дано: канал симметричного трапецеидального сечения, заложение откосов «m», ширина канала по дну «b», коэффициент шероховатости стенок «n», уклон дна канала «i» и расход «Q».
Требуется найти глубину наполнения канала «h», если движение в нем равномерное.
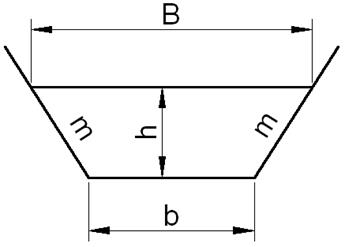
Рис. 11
Таблица 11.
|
№ Вар. |
Q м3/с |
m |
n |
в, м |
|
|
1 |
40 |
2.5 |
0.025 |
8.6 |
0.000078 |
|
2 |
40 |
2.5 |
0.025 |
8,6 |
0,041687 |
|
3 |
28 |
2,5 |
0,025 |
7,5 |
0,000085 |
|
4 |
28 |
2,5 |
0,025 |
7,5 |
0,046074 |
|
5 |
18,8 |
2,5 |
0,025 |
6,4 |
0,000100 |
|
6 |
18,8 |
2,5 |
0,025 |
6,4 |
0,054107 |
|
7 |
11,5 |
2,5 |
0,025 |
5,2 |
0,000068 |
|
8 |
11,5 |
2,5 |
0,025 |
5,2 |
0,078360 |
|
9 |
6,2 |
2,5 |
0,025 |
4,2 |
0,000072 |
|
10 |
6,2 |
2,5 |
0,025 |
4,2 |
0,082893 |
|
11 |
31,6 |
2,0 |
0,022 |
6,9 |
0,000062 |
|
12 |
31,6 |
2,0 |
0,022 |
6,9 |
0,031199 |
|
13 |
22,4 |
2,0 |
0,022 |
6,0 |
0,000070 |
|
14 |
22,4 |
2,0 |
0,022 |
6,0 |
0,035326 |
|
15 |
15,0 |
2,0 |
0,022 |
5,1 |
0,000081 |
|
16 |
15,0 |
2,0 |
0,022 |
5,1 |
0,041343 |
|
17 |
9,0 |
2,0 |
0,022 |
4,2 |
0,000052 |
|
18 |
9,0 |
2,0 |
0,022 |
4,2 |
0,055354 |
|
19 |
4,8 |
2,0 |
0,022 |
3,3 |
0,000056 |
|
20 |
4,8 |
2,0 |
0,022 |
3,3 |
0,059690 |
|
21 |
10,0 |
2,2 |
0,018 |
4,5 |
0,000120 |
|
22 |
10,0 |
2,2 |
0,018 |
4,5 |
0,062180 |
|
23 |
30,0 |
2,2 |
0,018 |
6,5 |
0,000105 |
|
24 |
30,0 |
2,2 |
0,018 |
6,5 |
0,051430 |
|
25 |
18,0 |
2,2 |
0,018 |
5,5 |
0,057250 |
Указания к решению задачи № 8
1. Находим модуль расхода, которым должен характеризоваться рассчитываемый канал. Этот модуль называется необходимым и обозначается Кнеобх..
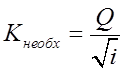
2. Составляем таблицу 12, в которой задаемся рядом значений h и для каждого h вычисляем соответствующий модуль расхода К.
3. По данным 1ой и 10ой строк таблицы строим график 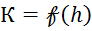 (рис.12).
(рис.12).
4. По этому графику, зная Кнеобх., находим искомое h, как показано на чертеже. Кривая ![]() имеет выпуклость обращенную в сторону оси h и проходит через начало координат (т. к. при h=0; К=0).
имеет выпуклость обращенную в сторону оси h и проходит через начало координат (т. к. при h=0; К=0).
Таблица 12
|
№ Стро—ки |
Величина или расчетная формула |
Едини—ца измере—ния |
Задаваемые и находимые численные значения |
Приме-чание |
||||
|
1 |
h |
м |
h1 |
h2 |
h3 |
…. |
…. |
|
|
2 |
mh |
м |
m = |
|||||
|
3 |
b + mh |
м |
b = |
|||||
|
4 |
|
м2 |
||||||
|
5 |
|
м |
||||||
|
6 |
|
м |
||||||
|
7 |
|
|
n= |
|||||
|
8 |
|
м3/с |
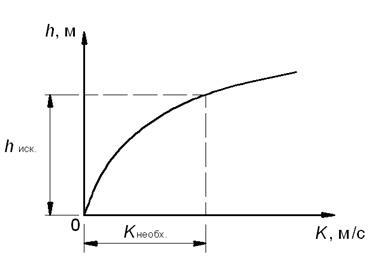
Рис. 12
Задача 9
Гидравлический расчёт малого моста с прямоугольным подмостовым руслом.
К малым относят мосты с пролётом до 25 м. Они вместе с дорожными трубами составляют большую часть (более 80% по численности) всех водопропускных сооружений на железных дорогах.
С точки зрения гидравлических требований малый мост должен удовлетворять двум основным условиям:
1. скорость потока под мостом не должна превышать допустимую скорость vдоп, которая устанавливается из условия неразмываемости грунта или определяется видом крепления подмостового русла;
2. должно быть обеспечено минимально допустимое превышение низа пролётного строения над уровнем поверхности воды перед мостом amin (запас).
Исходными данными для расчёта являются следующие величины: расчётный расход Q; глубина в русле hб, отвечающая расчётному расходу; высота расположения низа пролётного строения моста над дном русла Hм. Варианты заданий приведены в таблице 13.
Таблица 13
|
№ вар. |
Расчётный расход Q, м3/c |
Бытовая глубина hб, м |
Высота расположения низа пролётного строения Нм, м |
Коэффи-циент сжатия ε |
Коэффи-циент сопроти-вления ζ |
Вид грунта или крепления подмостового русла |
|
1 |
45,8 |
1,40 |
4,20 |
0,80 |
0,35 |
9 |
|
2 |
9,2 |
1,10 |
3,00 |
0,75 |
0,40 |
5 |
|
3 |
13,6 |
0,80 |
2,90 |
0,80 |
0,36 |
6 |
|
4 |
18,4 |
2,00 |
3,30 |
0,82 |
0,33 |
2 |
|
5 |
50,6 |
2,10 |
3,50 |
0,77 |
0,38 |
10 |
|
6 |
21,8 |
0,80 |
2,05 |
0,75 |
0,39 |
3 |
|
7 |
34,3 |
1,05 |
2,15 |
0,81 |
0,34 |
8 |
|
8 |
10,7 |
1,55 |
3,10 |
0,77 |
0,37 |
2 |
|
9 |
41,5 |
2,35 |
3,95 |
0,81 |
0,34 |
4 |
|
10 |
58,0 |
2,15 |
4,00 |
0,78 |
0,37 |
7 |
|
11 |
28,6 |
0,90 |
2,10 |
0,82 |
0,33 |
3 |
|
12 |
35,8 |
1,25 |
2,60 |
0,84 |
0,32 |
5 |
|
13 |
15,3 |
0,70 |
1,80 |
0,81 |
0,34 |
1 |
|
14 |
23,5 |
1,50 |
2,70 |
0,79 |
0,36 |
4 |
|
15 |
33,7 |
1,85 |
3,20 |
0,83 |
0,32 |
6 |
|
16 |
39,4 |
1,70 |
3,00 |
0,84 |
0,26 |
5 |
|
17 |
44,1 |
1,85 |
4,00 |
0,81 |
0,34 |
6 |
|
18 |
11,6 |
1,00 |
2,10 |
0,75 |
0,40 |
2 |
|
19 |
23,1 |
1,35 |
2,50 |
0,79 |
0,38 |
4 |
|
20 |
37,2 |
1,45 |
2,65 |
0,83 |
0,32 |
9 |
|
21 |
8,5 |
0,85 |
2,05 |
0,78 |
0,38 |
1 |
|
22 |
14,7 |
0,95 |
2,00 |
0,75 |
0,41 |
3 |
|
23 |
25,4 |
1,10 |
2,30 |
0,83 |
0,30 |
2 |
|
24 |
19,2 |
0,70 |
2,05 |
0,82 |
0,32 |
5 |
|
25 |
26,5 |
1,15 |
2,40 |
0,76 |
0,40 |
3 |
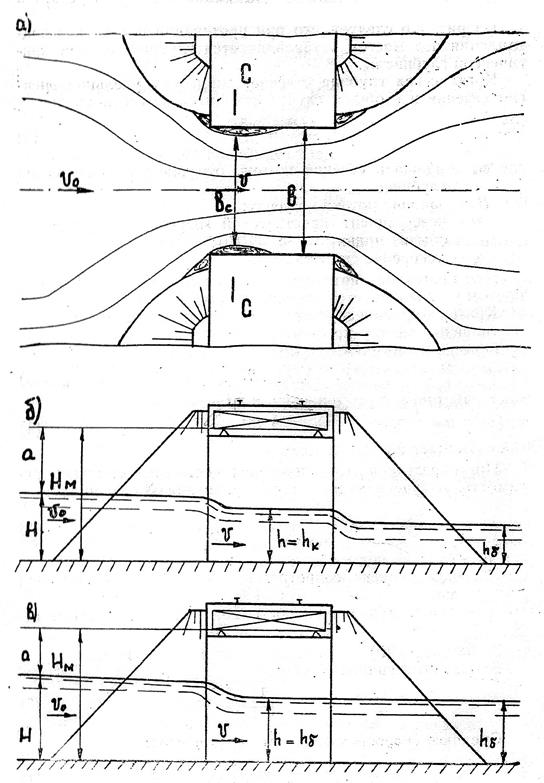
Рис. 1
На рис. 1 показана схема протекания потока под мостом. В позиции а показан план потока (буквами С – С обозначено сжатое сечение), в позиции б – разрез по оси потока при работе без подтопления; в позиции в – то же, при работе с подтоплением.
На рис. 1 введены следующие обозначения:
b – отверстие моста;
bc – ширина потока в сжатом сечении;
Hм – высота расположения низа пролётного строения над дном русла;
H – глубина перед мостом;
a – запас высоты низа пролётного строения над поверхностью воды перед мостом;
hб – бытовая глубина;
hк – критическая глубина;
h – глубина под мостом;
v – средняя скорость в подмостовом русле;
v0 – скорость подхода потока к мосту (в инженерных расчётах малых мостов эту скорость обычно не учитывают, принимая её равной нулю; это допущение идёт в запас расчёта).
Указания к решению задачи 9.
При гидравлическом расчёте малого моста следует придерживаться следующей последовательности.
1. Выбирают допустимую неразмывающую скорость vдоп исходя из характеристики грунта или вида крепления подмостового русла (см. прил. 6).
2. Вычисляют критическую глубину, соответствующую vдоп:
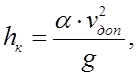
где величина корректива кинетической энергии α принимается равной 1,10.
3. Определяют схему работы моста и устанавливают глубину под мостом:
если
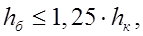
то мост не подтоплен и глубина под мостом равна критической
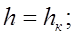
если
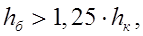
то мост подтоплен и глубина под мостом равна бытовой
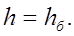
4. Определяют отверстие моста, соответствующее заданному расходу и полученной глубине:
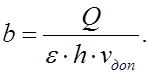
На основе полученного значения в качестве расчетного берут ближайшее большее типовое значение отверстия моста (см. табл. 14).
Табл. 14
|
Типовые отверстия малых мостов, м |
||||||||
|
2 |
3 |
4 |
5 |
6 |
7,5 |
10 |
12,5 |
20 |
Если вследствие небольшой величины vдоп отверстие моста получается больше максимального типового, то с целью уменьшения его следует рассмотреть варианты с различными типами крепления подмостового русла с соответствующим увеличением значений vдоп (см. строки 8, 9, 10 в приложении 6).
5. Определяют критическую глубину для принятого отверстия моста и проверяют схему протекания под мостом.
Критическую глубину находят по формуле:
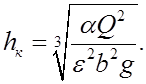
Схему протекания потока под мостом проверяют аналогично п. 3.
6. Вычисляют действительную скорость под мостом и проверяют условие неразмываемости подмостового русла.
Скорость под мостом
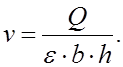
Эта скорость должна удовлетворять условию v < vдоп.
7. Определяют глубину воды перед мостом и проверяют условие по обеспечению минимального запаса amin от низа пролётного строения до поверхности воды.
Глубину воды перед мостом находят по формуле
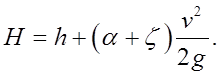
Затем вычисляют запас
a = Hм — H
и проверяют условие
a ≥ amin.
Значение amin в общем случае зависит от категории дороги, а в задаче принимается равным 0,5 м.
Если это условие не выполнено, то берут следующее большее типовое значение отверстия моста и проверяют расчёт.
8. Выполняют с соблюдением вертикального масштаба схему протекания потока через сооружение с указанием всех глубин и высоты расположения низа пролётного строения (вычерчивается по образцу схем б или в на рис. 1).
Приложения
Приложение 1
Методика расчета коэффициента гидравлического трения в напорных трубопроводах
|
Режим движения жидкости |
|||
|
Ламинарный |
Турбулентный |
||
|
Гидравлически гладкие трубы |
Гидравлически шероховатые трубы |
||
|
Область доквадратичного сопротивления |
Область квадратичного сопротивления |
||
|
Re < 2300 |
4000 < Re < 10 |
10 |
Re > 500 10 |
|
Формула Блазиуса |
Формула Альтшуля |
Формула Шифринсона |
|
|
|
|
|
|
|
λ=f (Re) |
λ=f (Re) |
λ=f (∆, Re) |
λ=f (∆) |
|
hℓ = A·V1 |
hℓ=B·V1,75 |
hℓ=C·V (1,75…2) |
hℓ=D·V2 |
Приложение 2
Кинематический коэффициент вязкости ν для воды в зависимости от температуры.
|
T,0C |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
|
ν, см2/с |
0,0178 |
0,0131 |
0,0101 |
0,009 |
0,0066 |
0,0058 |
0,0048 |
0,004 |
0,0086 |
0,003 |
Приложение 3
Плотность воды ρ в зависимости от температуры
|
T,0C |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
|
ρ, кг/м3 |
1000 |
999,6 |
998,9 |
998,2 |
996,9 |
995,6 |
993,9 |
992,2 |
990 |
988 |
985 |
983 |
Приложение 4
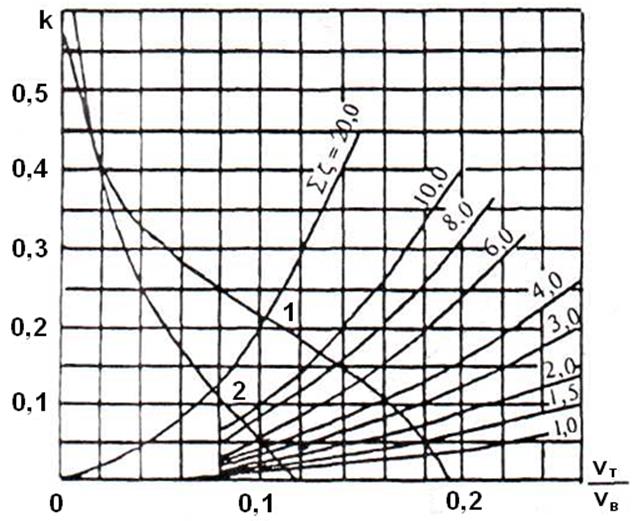
Зависимость k=k(vт/vв) для цилиндрической трубы (1), для трубы с оголовком, снабженным колпаком (2).
Приложение 5
Физические свойства сухого воздуха
(Рв=760 мм рт. ст. ![]() 1,01∙104 Па)
1,01∙104 Па)
|
t 0C |
кг/м3 |
t 0C |
кг/м3 |
t 0C |
кг/м3 |
|
-50 |
1,584 |
60 |
1,060 |
300 |
0,615 |
|
-40 |
1,515 |
70 |
1,029 |
350 |
0,566 |
|
-30 |
1,453 |
80 |
1,000 |
400 |
0,524 |
|
-20 |
1,395 |
90 |
0,972 |
500 |
0,456 |
|
-10 |
1,342 |
100 |
0,946 |
600 |
0,404 |
|
0 |
1,293 |
120 |
0,898 |
700 |
0,362 |
|
10 |
1,247 |
140 |
0,854 |
800 |
0,329 |
|
20 |
1,205 |
160 |
0,815 |
900 |
0,301 |
|
30 |
1,165 |
180 |
0,779 |
1000 |
0,277 |
|
40 |
1,128 |
200 |
0,746 |
1100 |
0,257 |
|
50 |
1,093 |
250 |
0,674 |
1200 |
0,239 |
Приложение 6
Допустимые неразмывающие скорости для различных типов грунтов.
|
Номер обозна-чения грунта |
Вид грунта или крепления подмостового русла |
Допустимая неразмывающая скорость, м/c |
|
Несвязные грунты |
||
|
1 |
Песок, ил |
0,15 – 0,20 |
|
2 |
Песок |
0,20 – 0,60 |
|
3 |
Гравий |
0,60 – 1,20 |
|
Связные грунты |
||
|
4 |
Супесь, суглинок |
0,7 – 1,0 |
|
5 |
Глина |
1,0 – 1,8 |
|
Скальные породы |
||
|
6 |
Осадочные |
2,5 – 4,5 |
|
7 |
Кристаллические |
20 – 25 |
|
Крепления |
||
|
8 |
Одиночное каменное мощение |
3,0 – 3,5 |
|
9 |
Двойное каменное мощение |
3,5 – 4,5 |
|
10 |
Бетонное покрытие |
5 – 10 |

 dэ = a
dэ = a