Инерциальная нелинейность, стабилизация амплитуды
|
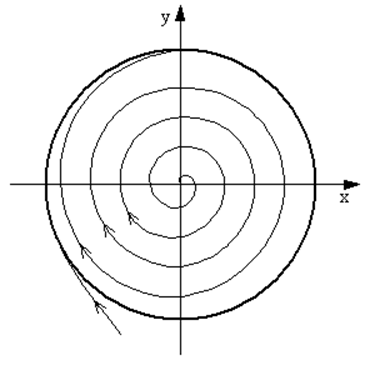
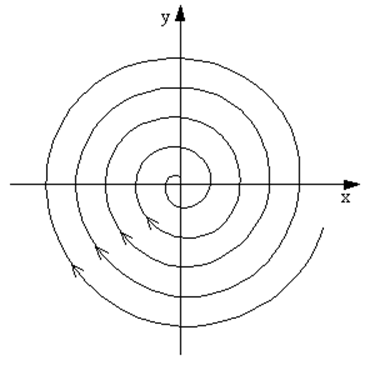
Рис. 46. Фазовый портрет автоколебательной системы томпсоновского типа при мягком режиме возбуждения для |
Рис. 47. Фазовый портрет автоколебательной системы томпсоновского типа при мягком режиме возбуждения для |
|
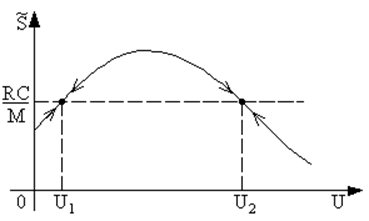
Выберем рабочую точку 2 где-то на изгибе характеристики, как показано на рис. 44, тогда зависимость усреднённой крутизны от амплитуды колебаний U будет немонотонной (рис. 48). При таком режиме возбуждения в потенциально автоколебательной системе не происходит самовозбуждения, т. е., если флуктуации (амплитуды толчков) в системе не превышают значения неустойчивой стационарной амплитуды U1, то эти флуктуации спадают до нуля. Поэтому для возбуждения |
Рис. 48. Кривая средней крутизны для случая, когда рабочая точка находится на изгибе ВАХ. |
автоколебательной системы с такой колебательной характеристикой необходимо сообщить ей толчок, величина которого U должна быть больше или равна U1 (жёсткое возбуждение).
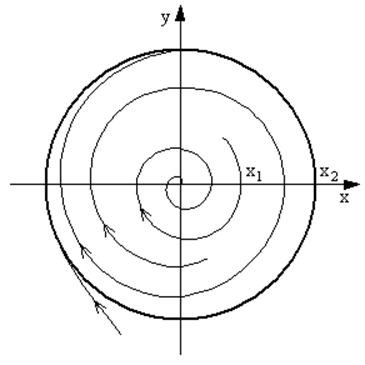
Качественное определение устойчивости стационарных амплитуд U1 и U2, аналогичное случаю мягкого режима, показывает, что решение U1 неустойчиво, а решение U2 устойчиво. Фазовый портрет для такого случая показан на рис. 49.
|
Рис. 49.Фазовые траектории автоколебательной системы томпсоновского типа при жёстком режиме возбуждения. |
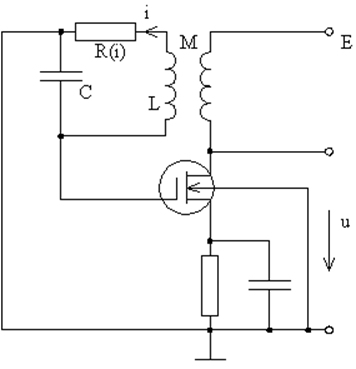
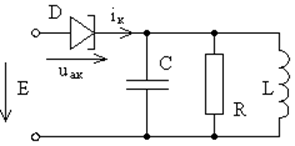
Применим теперь метод ММА к автоколебательным системам томпсоновского типа. На рис. 37 приведена обобщённая схема автоколебательной системы с активным элементом с характеристикой N-типа. В качестве такого элемента возьмём туннельный диод (рис. 50), ВАХ которого показан на рис. 9. Запишем уравнение Кирхгофа для токов в контуре
Из ВАХ (рис.9) видно, что i(uак = E) = i0. Введём новую переменную u = E — uак. При полиномиальной аппроксимации тока активного элемента получим
где a0 > 0, b0 < 0, g0 < 0. Тогда для нашей системы можно записать следующее уравнение движения: |
|
|
Рис. 50. Автоколебательная система, в которой в качестве активного элемента взят туннельный диод. |
|
(6.9) |
|
где |
||
системе при различных значениях её параметров. Если считать, что коэффициент регенерации k и коэффициенты нелинейности b и g удовлетворяют требованиям |k| << 1, |b| << 1, |g| << 1, то к такой системе применим метод ММА. Ищем решение в виде x(t) = u(t)cos(t) + v(t)sin(t), 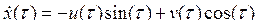 , тогда укороченные уравнения имеют вид
, тогда укороченные уравнения имеют вид
|
|
(6.10) |
где z = u2 + v2. Умножив первое из (6.10) на u, а второе на v и сложив их, получим
|
|
(6.11) |
В укороченных уравнениях (6.10) и (6.11) отсутствуют члены с коэффициентом b, откуда следует, что квадратичные члены при усреднении не влияют на процессы установления и стационарные амплитуды в таких автономных автоколебательных режимах работы.
Для этой системы существуют два стационарных решения (![]() ). Одно из них является нулевым решением и соответствует состоянию покоя u0 = v0 = z0 = 0, другое — с отличной от нуля амплитудой — имеет вид z0 = -4k/g. Так как заведомо z > 0, тогда, чтобы существовал предельный цикл, то необходимо k > 0. Проанализируем устойчивость стационарных состояний системы. Выберем некоторое отклонение x. В случае состояния покоя системы z = 0 + x, и тогда уравнение для возмущений в первом приближении имеет вид
). Одно из них является нулевым решением и соответствует состоянию покоя u0 = v0 = z0 = 0, другое — с отличной от нуля амплитудой — имеет вид z0 = -4k/g. Так как заведомо z > 0, тогда, чтобы существовал предельный цикл, то необходимо k > 0. Проанализируем устойчивость стационарных состояний системы. Выберем некоторое отклонение x. В случае состояния покоя системы z = 0 + x, и тогда уравнение для возмущений в первом приближении имеет вид ![]() . Таким образом, как видно, знак коэффициента регенерации k определяет устойчивость состояния покоя: при k > 0 (a > 2q) состояние покоя неустойчиво, происходит самовозбуждение; при k < 0 (a < 2q) состояние покоя устойчиво. В случае ненулевой стационарной амплитуды её значение при возмущении x запишется как z = -4k/g + x ; тогда уравнение для возмущения примет вид
. Таким образом, как видно, знак коэффициента регенерации k определяет устойчивость состояния покоя: при k > 0 (a > 2q) состояние покоя неустойчиво, происходит самовозбуждение; при k < 0 (a < 2q) состояние покоя устойчиво. В случае ненулевой стационарной амплитуды её значение при возмущении x запишется как z = -4k/g + x ; тогда уравнение для возмущения примет вид 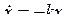 . При k > 0 (a > 2q) ненулевая стационарная амплитуда устойчива, при k < 0 (a < 2q) амплитуда неустойчива.
. При k > 0 (a > 2q) ненулевая стационарная амплитуда устойчива, при k < 0 (a < 2q) амплитуда неустойчива.
6.3. Инерциальная нелинейность, стабилизация амплитуды
|
Рис. 51. Генератор с термисторной стабилизацией амплитуды. |
Существуют элементы, параметры которых зависят не от мгновенных значений координат, а от амплитудных значений. Такие элементы называются инерционными нелинейностями, так как они принимают соответствующие значения не сразу, а через определённое время, называемое постоянной времени того или иного элемента. Примером такой нелинейности может служить обычное сопротивление, значение которого неизбежно зависит от протекающего по нему току. В силу тепловой инерции температура, а следовательно, и сопротивление такого резисторного элемента не являются мгновенной функцией протекающего по нему тока. Эти инерционные нелинейные активные элементы называются термисторами. Рефераты по физике сдают здесь
Другие статьиПохожая информацияУзнать стоимость за 15 минут
Распродажа дипломных
Подпишись на наш паблик в ВК
Нужна работа?
|
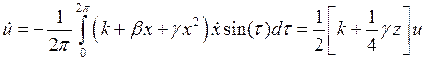 ,
,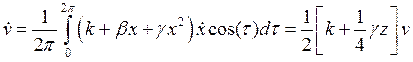
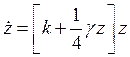 .
.