Интенсивность смещённой линии

А теперь попытаемся найти ответ на вопрос: почему интенсивность смещённой линии падает с увеличением номера химического элемента (рис. 92)?

Ответ на этот вопрос следует из рис. 86, где показан атом лития и его ядро N. Нетрудно видеть, что поверхность такого атома почти пуста и у рентгеновских фотонов имеется возможность взаимодействовать с отдельными электронами.

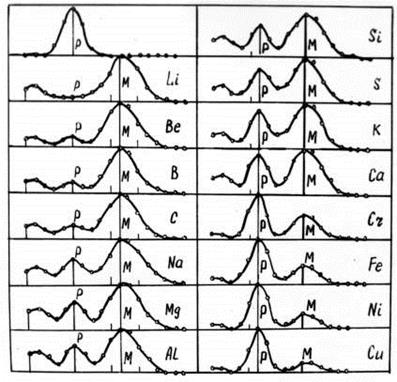
Рис. 92. Эффект Комптона на радиаторах различной Природы

При увеличении номера химического элемента увеличивается заполнение поверхностей атомов электронами, что затрудняет взаимодействие рентгеновских фотонов с отдельными электронами. В результате интенсивность смещенной линии (рис. 92) уменьшается.

Если представить атом меди, ядро которого показано на рис. 93, a, то его поверхность заполнена электронами полнее (рис. 93, b), что затрудняет взаимодействие рентгеновских фотонов с отдельными электронами и интенсивность смещенной линии уменьшается, что и наблюдается на рис. 92.

У нас есть основания представить поверхность многоэлектронного атома в виде одуванчика (рис. 93, b). Тогда поверхность такого атома, заполненная электронами, будет близка к сферической, когда он находится в невозбуждённом состоянии. Когда же один из его электронов поглощает фотон, то энергия связи такого электрона с ядром уменьшается, в результате он удаляется от ядра и от общей сферической поверхности атома. В таком состоянии он становится активным – готовым вступить в связь с аналогичным электроном другого атома. Так образуется молекула [2].

а)	b) Рис. 93. (a – модель ядра атома меди; (b) – возможная архитектоника поверхности многоэлектронного атома

Конечно, соединение произойдёт лишь с тем электроном соседнего атома, который будет удалён от его поверхности и у которого свободным будет противоположный магнитный полюс. Указанные два электрона и являются валентными электронами.

Таким образом, сравнивая поверхности атома лития (рис. 86) и атома меди (рис. 93, b), видим значительную возможность рентгеновских фотонов взаимодействовать индивидуально с электронами атома лития и меньшую — с электронами атома меди. Экспериментальные данные, представленные на рис. 92, убедительно подтверждают это.

Достоверность этого доказательства усиливается путём аналитического вывода формулы Комптона из схемы (рис. 94) взаимодействия кольцевых моделей фотонов (рис. 84, 94) и электронов (рис. 1) [2].

Импульс 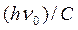падающего на электрон фотона и импульс 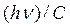отраженного от электрона фотона связаны простой зависимостью (рис. 94)

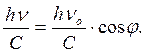(62)

После взаимодействия фотона с электроном его импульс изменится на величину

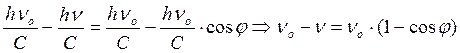. (63)

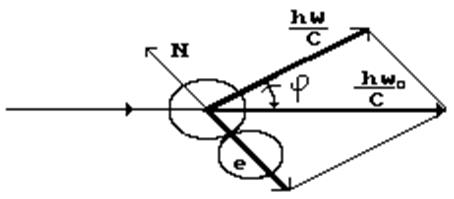
Рис. 94. Схема взаимодействия фотона с электроном в эффекте Комптона

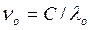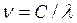Поскольку и , то

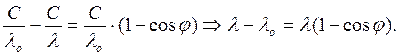
(64)

Известно, что эффект Комптона проявляется при взаимодействии между электронами и рентгеновскими фотонами. Это обусловлено тем, что они имеют близкие по величине радиусы, поэтому у нас есть основания обозначить 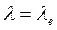. Полагая также, что , имеем [2]

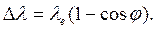(65)

Это и есть формула Комптона для расчета изменения длины волны отраженного рентгеновского фотона, которую он подобрал эмпирически в 1922 году и использовал при интерпретации результатов своего эксперимента.

Обозначая массу фотона до отражения через 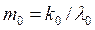, а после отражения – через 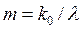и учитывая, что

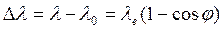, (66)

найдём

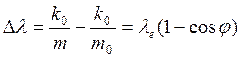, (67)

или

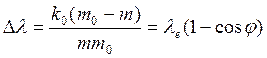. (68)

Если 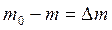, то

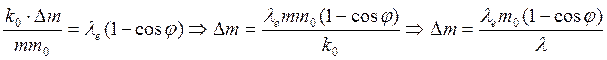. (69)

Длина волны рентгеновских фотонов, использованных в эксперименте, 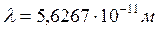. Константа локализации позволяет определить их массу

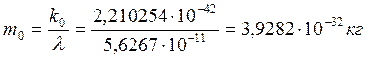. (70)

Поскольку угол может изменяться в интервале 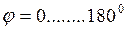, то для расчётов возьмём его среднее значение 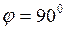. Тогда

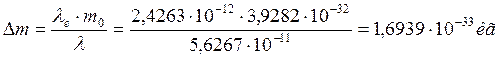. (71)

Таким образом, рентгеновский фотон, взаимодействуя с электроном под углом , потерял

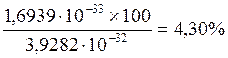(72)

своей массы. Тем не менее, если бы из потерянной массы сформировался фотон, то он имел бы радиус

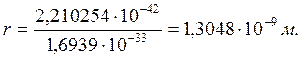(73)

Как видно, масса (71), потерянная отражённым рентгеновским фотоном, эквивалентна массе рентгеновского фотона [2].

Сразу возникает вопрос: куда девалась масса, потерянная отражённым рентгеновским фотоном, если она не сформировалась в соответствующий фотон? Конечно, если бы она сформировалась в соответствующий фотон, то приборы обязательно зарегистрировали бы его. Однако чёткой информации об этом нет, поэтому у нас появляются веские основания полагать, что масса, потерянная отражённым фотоном, не оформившись ни в какую частицу, растворилась в пространстве, приняв форму и свойства эфира. В результате закон сохранения энергии не соблюдается.