Инвариантная масса системы частиц

Задача 3. Ядро железа при переходе из возбужденного состояния в основное излучает фотоны с энергией 14.4 КэВ. Определите уменьшение частоты фотона на каждый километр высоты при его распространении снизу вверх.

Опыт по измерению изменения частоты излучения ядер железа часто называют взвешиванием фотонов.

3. Когда возможно рождение новых частиц

3.1 Инвариантная масса системы частиц

Инвариантной массой M нескольких частиц называют полную массу, измеренную в системе центра масс, т. е. в такой системе отсчета, в которой полный импульс всех частиц равен нулю. Если в какой-нибудь системе отсчета известны энергии всех частиц En и известны их импульсы — , то инвариантную массу можно найти по определению

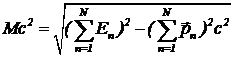. (9)

Например, инвариантная масса двух частиц равна

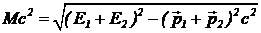. (10)

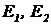и – энергии и импульсы частиц. Надо иметь в виду, что под радикалом производится векторное суммирование импульсов, поэтому при одной и той же энергии частиц могут получаться разные инвариантные массы при разных взаимных ориентациях импульсов.

Задача 4. Частицы с инвариантными массами m01 и m02 имеют энергии соответственно E1 и E2, а импульсы — и . При каких взаимных ориентациях импульсов инвариантная масса пары частиц имеет максимальное и минимальное значения? Чему равны эти значения?

При столкновении двух частиц с большой инвариантной массой пары могут рождаться новые тяжелые частицы. Рождение новых частиц не должно нарушать никакого закона сохранения (энергии, импульса, заряда и т. д.). Например, при рассеянии двух фотонов подходящей энергии друг на друге может родиться пара частиц — электрон и позитрон.

Задача 5. Определите максимальное и минимальное значения инвариантной массы пары одинаковых фотонов с одинаковой энергией E. Чему должно равняться минимальное значение энергии, чтобы могла родиться электрон-позитронная пара? Масса позитрона равна массе электрона и равна 9.1×10-31кг (=0,51 МэВ).

Задача 6. Определите инвариантные массы пары электронов с энергиями по 1 ГэВ при следующих значениях угла J между направлениями импульсов:
а) J1=0;
б) J2=;
в) J3=;
г) J4=p;

4. Домашнее задание

4.2 Решение задач

Задача 1. Вычислите электромагнитную добавку к массе протона в предположении, что его заряд равномерно распределен по сфере радиуса 10-15м.

Задача 2. Пучок ультрарелятивистских электронов с энергией 10 ГэВ пролетает вблизи Солнца. На какой угол от первоначального направления движения отклонится пучок? Завышенное или заниженное значение угла получилось бы, если бы расчет проводился в рамках ньютоновской механики?

Задача 3. Для исследования структуры элементарных частиц (например, протонов) приходится использовать налетающие частицы как можно большей энергии. Почему оказывается невыгодным проводить опыты, в которых исследуемые частицы являются неподвижными мишенями, а на них направляется поток разогнанных частиц? Почему более выгодными являются опыты на встречных пучках?

Задача 4. Какую минимальную энергию (в электронвольтах) должны иметь протоны во встречных пучках, чтобы при их столкновении могли дополнительно родиться еще один протон и один антипротон (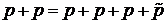)? Масса антипротона равна массе протона и равна 1.67 10-27 кг (=938 МэВ).

занятие 1.6.4

решение задач

1.Качественные задачи

1.2.1 Почему нейтральный пион легче заряженного пиона?

1.2.2 Всегда ли свет в вакууме распространяется прямолинейно?

1.2.3 Астрофизики предсказывают, что если звезда имеет массу, большую массы Солнца в 10 раз, то по мере остывания она превратится в “черную дыру”, замечательную тем, что никакими оптическими приборами ее нельзя будет обнаружить. Поясните это утверждение.

1.2.4 Почему масса ядра меньше суммарной массы составляющих его частиц?

1.2.5 Существует теория, согласно которой полная масса астрономического объекта может равняться нулю. Как такое может быть?

1.2.6 Как определяется инвариантная масса системы частиц?

1.2.7 Зависит ли инвариантная масса системы частиц от выбора системы отсчета?

1.2.8 Может ли электрон, движущийся равномерно прямолинейно с большой скоростью, излучить фотон?

1.2.9 Может ли свободный электрон поглотить фотон?

1.2.10 Может ли свободный фотон с энергией 2 МэВ распасться на электрон и позитрон, если энергия покоя электрона равна энергии покоя позитрона и равна 0,51 МэВ?

1.2.11 Можно сформулировать условие распада частицы, аналогичное закону сохранения энергии. Сформулируйте его.

2. Решение задач

2.1 Измерения масс нейтральных частиц

Информацию об инвариантных массах, о временах жизни многих заряженных частиц можно получить из расшифровки следов в трековых камерах. Для этого достаточно измерить энергию частицы (по толщине следа), импульс (по радиусу кривизны трека в магнитном поле), время жизни в лабораторной системе отсчета (по длине следа от рождения до распада). Как быть с нейтральными частицами, которые следов не оставляют? Инвариантная масса нейтральной частицы может быть определена по трекам заряженных частиц, на которые она позднее распадается. Например, нейтральный пион может распадаться на электрон и позитрон. По трекам электрона и позитрона можно определить их энергии и импульсы. А поскольку инвариантная масса сохраняется (инвариантная масса пары электрон-позитрон равна инвариантной массе того, что распалось на эти частицы), подстановка полученных значений в выражение инвариантной массы пары даст инвариантную массы нейтрального пиона.

Задача 1. В пузырьковой камере обнаружен характерный след — вилка, который можно трактовать как распад нейтральной частицы на электрон и позитрон. Угол разлета электрона и позитрона оказался равным 1200. По радиусу кривизны треков определили, что импульсы частиц одинаковы и, измеренные в единицах pc, равны 77,94 МэВ. Чему равна инвариантная масса распавшейся частицы, если энергии покоя электрона и позитрона равны по 0,51 МэВ?

Задача 2. Вскоре после открытия нейтрона было установлено, что он нестабилен. В трековых камерах после распада нейтрона оставались следы электрона и протона. Так, например, после распада покоящегося нейтрона могли возникать такие ситуации: следы электрона и протона составляют угол 900, импульс протона ppc=0,515 МэВ, импульс электрона pec=0,40 МэВ. Какие выводы следовало сделать из этих фактов?

Решение. Если распавшийся нейтрон покоился, полный импульс до и после распада равен нулю. Но сумма импульсов протона и электрона не равна нулю, значит, среди продуктов распада была еще одна, незарегистрированная частица с импульсом, равным по модулю сумме импульсов протона и электрона и противоположно направленным: 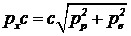= 0,652 МэВ. Энергии, уносимые протоном и электроном: 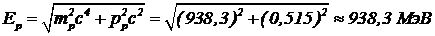; 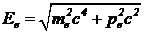= 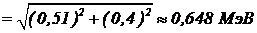. Начальная энергия нейтрона равна En=939,6 МэВ. Таким образом, на неизвестную распадную частицу приходится Ex=939,6-938,3–0,648» 0,652 Мэв. Инвариантная масса неизвестной частицы равна

История такого рода экспериментов является историей открытия новой частицы — нейтрино, которую долгое время не могли экспериментально обнаружить.