Критерий рейнольдса

Линейные потери водопроводных систем определяются так же по зависимости

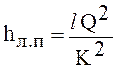, (5.7)

где l — длина расчетного участка; Q — расход по участку; К — расходная характеристика, берется из таблиц в зависимости от материала трубопровода и его диаметра.

рассмотрим особенности расчета безнапорных систем, каковыми являются каналы, лотки и т. п. устройства.

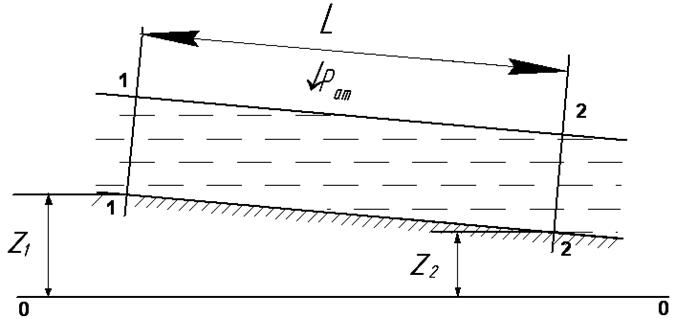
Рис.5.2

При равномерном движении жидкости в подобных системах уравнение Бернулли для потока реальной жидкости, составленное для сечений 1-1 и 2-2 (рис.5.2) имеет вид

,

т. е. разница геометрических напоров затрачивается на преодоление линейных потерь. Таким образомт движение жидкости обеспечивается наличием гидравлического уклона i, который в данном случае равен геометрическому:

.

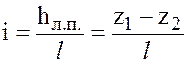Поэтому при проектировании каналов большой протяженности используют естественный уклон местности и в этом случае определяют пропускную способность канала и его размеры по формуле Шези:

, (5.8)

где — живое сечение канала; R — гидравлический радиус; С — коэффициент Шези, который зависит от гидравлического радиуса и коэффициента шероховатости.

Коэффициент Шези берется из таблиц или определяется по формулам, например, по формуле Маннинга

.

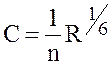При необходимости решаются и другие задачи.

Местные потери. Для их определения пользуются единственной формулой

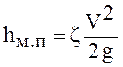, (5.9)

где — коэффициент местного сопротивления, берется из таблиц и графиков, вычисляется по специальным формулам в зависимости от вида местного сопротивления; V — скорость движения жидкости в трубопроводе, где установлено местное сопротивление.

5.4. режимы движения жидкости. критерий рейнольдса

Гидравлические потери существенным образом зависят от того, как организовано движение жидкости в потоке, т. е. от режима движения жидкости.

Из физики известно, что существует два режима движения жидкости: ламинарный и турбулентный. Эти термины в науку ввел Д. И. Менделеев.

Слово «ламинарный» — от латинского «ламина», что означает «слой», т. е. ламинарный режим это слоистое течение без перемешивания частиц и пульсации скорости.

Слово «турбулентный» — от латинского «турбулус», означает беспорядочный, хаотичный, т. е. турбулентный режим движения жидкости сопровождается интенсивным перемешиванием жидкости, пульсациями скоростей и давлений.

Более полно режимы движения жидкости исследованы английским физиком Осборном Рейнольдсом.

Визуальное наблюдение за режимами движения жидкости и их количественная оценка были выполнены на установке (рис.5.3), представляющей собой резервуар 1, из которого жидкость по прозрачной трубе 2 с краном может вытекать в мерное устройство 3. над резервуаром помещен сосуд 4 с подкрашенной жидкостью, для подачи последней по капилляру в прозрачную трубу.

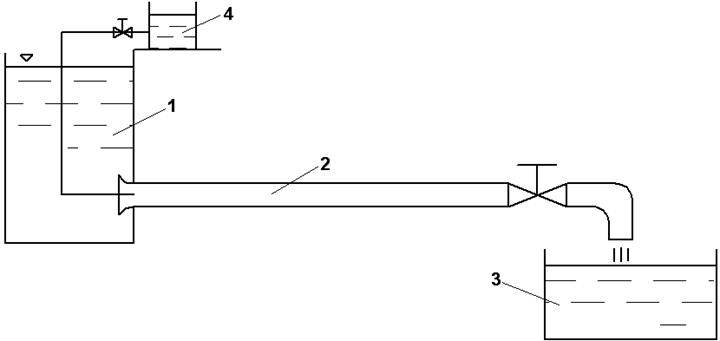
Рис.5.3

Рейнольдс установил факторы, влияющие на режим движения жидкости: скорость, диаметр трубки, плотность и вязкость жидкости, на основании чего ему удалось определить критерий (критерий Рейнольдса), по которому можно судить о режиме движения жидкости:

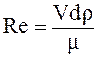или 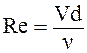. (5.10)

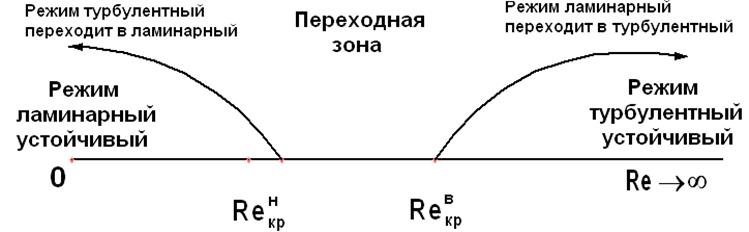
Рис.5.4

Возьмем ось чисел Рейнольдса (рис.5.4) и повторим его опыты сначала в сторону увеличения этих чисел, одновременно визуально наблюдая за режимами движения жидкости. При достижении так называемого верхнего критического числа режим ламинарный прейдет в турбулентный. В зависимости от условий эксперимента это число может лежать в довольно больших пределах: от 4·103 до (40…50)·103. После этого числа режим становится турбулентным устойчивым.

Затем повторим опыт в сторону уменьшения чисел Рейнольдса. В этом случае турбулентный режим перейдет в ламинарный при достижении так называемого нижнего критического числа . Оно окажется равным 2320. Ниже этого числа режим всегда будет ламинарный устойчивый. Нижнее критическое число принимают вообще за критическое число. в гидравлических расчетах при получении Re < 2320 режим считают ламинарным, при Re > 2320 — турбулентным.

Физический смысл этого критерия заключается в том, что он показывает отношение сил инерции к силам трения.

Этот критерий является критерием гидродинамического подобия, о чем более подробно будет изложено ниже.

Число Рейнольдса может быть подсчитано для потоков любого геометрического сечения, в том числе для круглого по гидравлическому радиусу, или по другому характерному размеру, например, по зазору в сопрягаемых деталях.

5.5. Особенности ламинарного режима движения жидкости

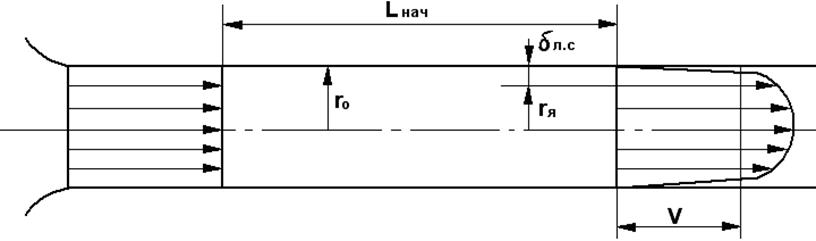
Рассмотрим формирование ламинарного потока в трубопроводе круглого сечения с плавным входом. Жидкость поступает в трубопровод с почти одинаковой скоростью по всему сечению. По мере удаления от входа толщина заторможенного слоя жидкости у стенки увеличивается. Но так как расход жидкости остается одним и тем же, то замедление слоев, расположенных ближе к стенкам, вызывает увеличение скорости слоев, расположенных ближе к оси (рис.5.5).

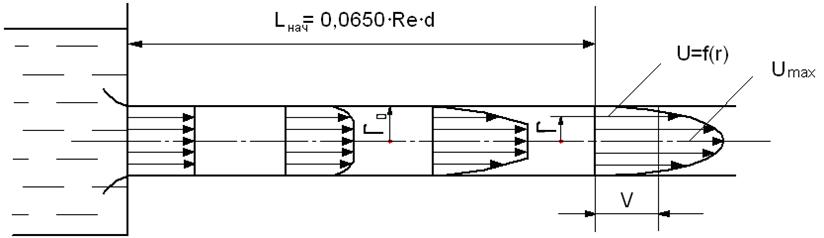
Рис.5.5

Длина входного участка, на котором заканчивается формирование потока, называется длиной начального участка. За начальным участком движение становится равномерным, поэтому все измерительные устройства следует устанавливать за начальным участком.

Эпюра скорости в сформировавшемся ламинарном движении имеет вид квадратичной параболы, у которой закон распределения скорости

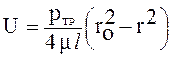, (5.11)

где ртр — потери давления по длине участка l; — динамическая вязкость.

Из выражения (5.11) следует, что максимальная скорость будет при r = 0, т. е. по оси трубопровода, а средняя .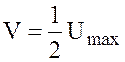

Величина линейных потерь при ламинарном режиме определяется по формуле Пуазейля

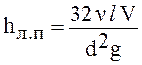. (5.12)

Следовательно, линейные потери при ламинарном режиме пропорциональны скорости в первой степени. Это имеет принципиальное значение. Но в формуле (5.5) линейные потери пропорциональны скорости в квадрате. формулы же (5.5) и (5.12) идентичны. В формуле (5.5) коэффициент гидравлического трения должен быть определен по формуле Пуазейля: λ = 64/Re. Вспомнив, что критерий Рейнольдса определяется по зависимости Re = Vd|υ, и подставив выражение 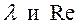в формулу (5.5), получим выражение (5.12).

Ламинарный режим имеет место при движении жидкости в капиллярах в естественных условиях почвогрунтах или в устройствах для осветления жидкости (фильтрах, сепараторах, центрифугах), т. е. в тех случаях, где перемешивание жидкостей недопустимо.

5.6. Особенности турбулентного режима движения жидкости

Рассмотрим формирование потока при турбулентном движении жидкости в трубопроводе круглого сечения радиусом rо с плавным входом (рис.5.6).