Квазистационарные явления в электрических цепях

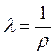. (9.2)

Запись закона Ома для однородного участка цепи имеет вид

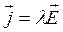, (9.3)

для неоднородного –

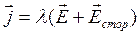, (9.4)

где – плотность тока.

Закон Джоуля-Ленца в дифференциальной форме связывает тепловую мощность, выделяемую в единице объема проводника с плотностью тока и напряженностью электрического поля –

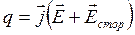. (9.5)

Темы для развернутых ответов

1.  Закон Ома в дифференциальной и интегральной формах.

2.  Закон Джоуля-Ленца в дифференциальной и интегральной формах.

Литература: [1], глава 2, §16, глава 4, §26-27; [3], глава 3, §35-38.

Основной блок задач

1.  Найти сопротивление среды току между двумя концентрическими электродами радиусами и (). Удельная проводимость среды равна .

2.  Между двумя плоскими электродами площади каждый, линейные размеры которых много больше расстояния между ними, находится проводящий материал, удельная проводимость которого изменяется линейно от до у разных поверхностей. Найдите сопротивление среды между электродами.

3.  Найдите сопротивление конического проводника кругового сечения, основания которого имеют радиусы и . Проводимость среды равна .

4.  Полусферический заземлитель погружен в землю вровень с ее поверхностью. Найти напряжение, под которым может оказаться человек, приближающийся к заземлителю (шаговое напряжение). Сила тока , протекающего через заземлитель, задана. Длина шага равна , расстояние от ближней к заземлителю ноги человека до него равно . Рассчитайте шаговое напряжение при условии, что , , , .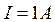

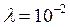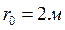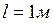Дополнительный блок задач

5.  Длинный проводник круглого сечения радиуса сделан из материала, удельное сопротивление которого зависит только от расстояния до оси проводника по закону 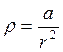. Найдите сопротивление единицы длины проводника и напряженность электрического поля, если по проводнику течет ток . Какая мощность выделяется в проводнике?

6.  Провод длиной , по которому течет ток , упал со столба на землю. Найти шаговое напряжение, если известно, что длина шага , расстояние от провода до ближайшей ноги . Найдите ответ, учитывая следующие данные: , , , .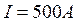

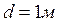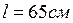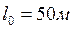Практическое занятие №12

Квазистационарные явления в электрических цепях

Краткие теоретические сведения

При изучении переменных полей и токов необходимо принимать во внимание конечность скорости распространения электромагнитных полей и наличие объемной плотности тока смещения

. ()

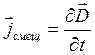При некоторых условиях этими факторами можно пренебречь. Токи и поля, удовлетворяющие этим условиям, называются квазистационарными.

Длина волны периодического процесса, распространяющегося со скоростью , равна 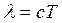. Если линейные размеры области, в которой мы рассматриваем данный процесс удовлетворяют условию , то конечностью скорости распространения процесса можем пренебречь.

Если ток смещения много меньше тока проводимост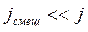и , или 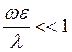, то можно считать квазистационарными переменные процессы вплоть до частот 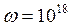с-1 (в проводниках, но не в вакууме).

В электрических цепях с ЭДС , индуктивностью и емкостью закон Ома может быть записан в следующей форме –