Лекции по динамике

Лекция 1

Введение. Динамические нагрузки, возникающие в процессе работы транспортной техники

Транспортная техника должна соответствовать выполняемым ею технологическим процессам, высоким технико-экономическим показателям. Однако повышение этих показателей, в свою очередь, вызывает увеличение скоростей движения рабочих органов, сокращение периодов их разгона и торможения. Данные факторы способствуют увеличению динамических нагрузок в элементах конструкции машин и могут препятствовать снижению веса и улучшению других показателей.

По режиму работы транспортная техника подразделяется на подъемно-транспортные, землеройно-транспортные, строительно-дорожные машины, тракторы и автомобили.

Подъемно-транспортные машины подразделяются на два основных класса: грузоподъемные, работающие в периодическом режиме и предназначенные для перемещения грузов по вертикали и передачи их из одной точки площади, обслуживаемой машиной, в другую; машины непрерывного транспорта, работающие в непрерывном режиме и предназначенные для перемещения грузов по заданной трассе и других работ.

Землеройно-транспортные машины применяются как простые, но высокоэффективные средства механизации на земляных работах в строительной, горнорудной и других отраслях промышленности. К ним относятся бульдозеры, скреперы, автогрейдеры.

Строительно-дорожные машины применяют для механизации и автоматизации погрузочно-разгрузочных, транспортных работ, дорожного строительства. Они подразделяются на погрузочно-разгрузочные, землеройные, дорожные машины. К землеройным машинам относятся одноковшовые и многоковшовые экскаваторы, шагающие драглайны.

Тракторы и автомобили предназначены, в основном, для механизации транспортных операций в строительстве и различных отраслях промышленности. Данные машины подразделяются на следующие классы: грузовые автомобили, тракторы гусеничные и колесные, пневмоколесные тягачи, специализированные транспортные средства.

Установлено, что 60% отказов современной транспортной техники, в основном, связано с динамическими нагрузками, которые приводят к повышенному изнашиванию трущихся элементов, усталостному разрушению несущих металлоконструкций и деталей механизмов, появлению недопустимых остаточных деформаций и т. п.

Для исследования динамики реальную машину заменяют физической моделью, представляющей собой несколько сосредоточенных масс (ротор двигателя, тормозной шкив, рабочие звенья), соединенных упругими безмассовыми связями (канаты, валы, ленты и др.). Под действием внешних нагрузок (моментов электродвигателей и тормозов, сопротивлений рабочей машины) упругие элементы деформируются, а сосредоточенные массы машин, кроме основного движения, совершают малые колебания.

Во многих механизмах транспортной техники динамические нагрузки имеют решающее значение. Знание действительных нагрузок позволяет создавать надежные конструкции машин с улучшенными параметрами, а при эксплуатации – достигать наибольшей производительности обоснованным использованием резервов прочности и мощности.

Основная литература [3, c.317…319]

Дополнительная литература [10, c.31…34]

Контрольные вопросы:

1. Приведите классификацию транспортной техники по режиму работы.

2. Что представляет собой физическая модель, которой заменяют реальную машину для исследований динамики?

3. Какова главная цель динамических расчетов транспортной техники?

Лекция 2

Составление расчетных динамических схем машин и механизмов. Приведение сил, масс, моментов инерции, жесткостей

Динамический расчет начинают с составления расчетной динамической схемы машины и уравнений движения масс, входящих в эту схему. От реальной машины к расчетной динамической схеме переходят, пренебрегая теми физическими факторами, которые для конкретного расчетного режима имеют несущественное значение.

Выбор той или иной расчетной схемы определяется задачей расчета. В расчетных динамических схемах реальные параметры машин (масса, коэффициенты жесткости, податливости и т. п.), а также внешние нагрузки заменяют приведенными величинами для упрощения расчетных уравнений и соот ношений. Приведение параметров и нагрузок производят на основании равенства общей энергии приведенной системы. Приведение производится либо к поступательному движению, либо к вращательному движению одной из масс механизма.

Критерием достоверности принятой расчетной схемы является опыт, сравнение теоретического расчета с результатами эксперимента.

Приведенные силы определяют из условия равенства их работы сумме работ тех сил, которые они заменяют, т. е.

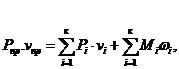
где приведенная сила; проекция действующей на i—e звено силы на направление движения центра масс этого звена; момент, действующий на i—e звено.

Из этого уравнения находим:

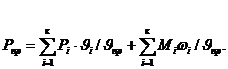(2.1)

Приведенная масса и приведенный момент инерции определяются из условия равенства кинетической энергии приведенной массы сумме кинетических энергий масс, которые она заменяет. Аналитически это правило выражается уравнениями:

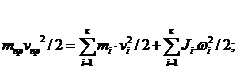
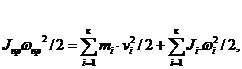
где mпр и Jпр — приведенная масса и приведенный момент инерции; и -линейная и угловая скорости звена приведения; mi u Ji — масса и момент инерции i — го звена механизма; и — линейная и угловая скорости i — го звена механизма.

Из этих уравнений находим

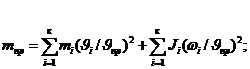(2.2)

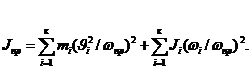(2.3)

Приведение жесткостей выполняется так, чтобы потенциальная энергия приведенной системы равнялась потенциальной энергии реальной упругой системы.

Пусть имеется система из двух валов с жесткостью C1 и С2, соединенных между собой зубчатой передачей (рис. 2.1, a), которую требуется заменить системой с одним упругим элементом, имеющим приведенную жесткость Спр (рис.2.1, b), причем, жесткости следует привести к валу 1.

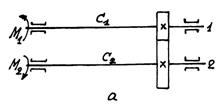
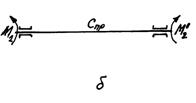
Рисунок 2.1 — Схема к приведению жесткостей двух валов с зубчатой передачей к жесткости одного вала

Если к валу 1 приложен момент M1, то момент, приложенный к валу 2, M2 = M1.U; в приведенной системе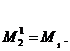

В нашем примере: потенциальная энергия реальной системы

П = М1.φ1 /2 + М2. φ 2 /2 = М1(φ 1 + φ 2.U) /2,

где φ1 , φ2.- углы закручивания валов под действием приложенных к ним моментов, причем φ1 = M1/C1; φ2 = M2/C2; U — передаточное число зубчатой передачи.

Потенциальная энергия приведенной системы

П = М1. φ пр /2,

где φ пр — угол закручивания приведенной системы.

Приравнивая два выражения потенциальной энергии, получаем

φ пр = φ 1 + φ 2.U. (2.4)

Согласно определению, приведенная жесткость

Cпр= М1/ φ пр = М1/( φ 1 + φ 2.U) .

Подставляя в это уравнение значения М1 = φ1.С1 и φ 2 = φ 1C1U/C2,

получаем 1/Cпр = 1/C1 + U2/C2 или Cпр = C1 . C2 / (С1U2 + C2). (2.5)

Основная литература [3, c. 319…325]

Дополнительная литература [10, c. 34…36]

Контрольные вопросы:

1. Сколько масс и какой способ соединения между ними должна содержать расчетная динамическая схема?

2. К какому виду движения одной из масс механизма производится приведение параметров машин и внешних нагрузок?

3. Приведите зависимости для определения приведенных сил, масс, моментов инерции и жесткостей.

Лекция 3

Общие уравнения динамики машин и механизмов

Динамические нагрузки в упругих элементах механизмов и машин определяют из дифференциальных уравнений движения масс, причем число уравнений, подлежащих совместному решению, равно числу степеней свободы системы. Дифференциальные уравнения движения системы можно составить различными методами: Даламбера, Лагранжа, Эйлера-Ньютона и другими.