принцип даламбера
Согласно принципу Даламбера, в любой момент времени имеет место равновесие сил инерции, активных внешных сил и сил реакции связей находящейся в движении системы.
В этом случае необходимым и достаточным условием равновесия является равенство нулю геометрической суммы сил и суммы моментов этих сил относительно произвольной точки A, т. е.
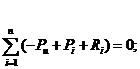 (3.1)
(3.1)
![]() (3.2)
(3.2)
где Pu = mi. ai — сила инерции; Pi — активная сила; Ri — реакция связи, приложенная к произвольной массе системы.
Недостатком принципа Даламбера является то, что для его использования требуется учет направления действия сил инерции и действующих ускорений, что не всегда возможно.
Наиболее общим и простым методом решения задач динамики для несвободных систем является метод Лагранжа, основанный на понятии обобщенных координат. Для получения дифференциальных уравнений движения методом Лагранжа необходимо составить выражение для кинетической и потенциальной энергии системы в функции выбранных обобщенных координат.
Уравнение Лагранжа для обобщенной координаты x имеет вид
![]() (3.3)
(3.3)
где ![]() обобщенная скорость:
обобщенная скорость: ![]() ; К и П — соответственно кинетическая и потенциальная энергии исследуемой системы; Px — движущая обобщенная сила.
; К и П — соответственно кинетическая и потенциальная энергии исследуемой системы; Px — движущая обобщенная сила.
Кинетическая энергия вращающихся и поступательно движущихся масс
![]()
где ![]()
![]() и
и ![]() соответственно момент инерции, угол поворота и угловая скорость любого вращающегося элемента относительно оси его вращения; m, S и
соответственно момент инерции, угол поворота и угловая скорость любого вращающегося элемента относительно оси его вращения; m, S и ![]() соответственно масса, путь и линейная скорость любого поступательно движущегося элемента рассматриваемой системы.
соответственно масса, путь и линейная скорость любого поступательно движущегося элемента рассматриваемой системы.
Потенциальная энергия системы
![]()
где C и K — угловая (при кручении) и линейная жесткости элемента x системы; ![]() и S — угол закручивания и перемещение элемента x.
и S — угол закручивания и перемещение элемента x.
С понятием обобщенной координаты x связано понятие обобщенной силы Px. Эта сила равна частному от деления элементарной работы dA, производимой всеми силами (как внутренними, так и внешними), действующими на систему, на бесконечно малое приращение обобщенной координаты dx:
Px = dA/dx.
При составлении уравнений движения системы распределенные массы заменяют сосредоточенными, а рассредоточенные – приведенными.
Основная литература [3, c. 326…330]
Дополнительная литература [10, c. 47…50]
Контрольные вопросы:
1. В чем заключается принцип Даламбера? Назовите его недостаток.
2. Напишите уравнение Лагранжа.
3. От каких параметров зависят кинетическая и потенциальная энергии системы?
Лекция 4
Динамика подъема и опускания грузов кранами при переходных режимах работы механизмов
Динамические нагрузки, возникающие в процессе подъема или опускания груза, зависят от того, как производится подъем груза – «с веса» или «с подхватом».
В первом случае нагружения предполагается, что груз уже приподнят и статическая нагрузка на подъемный канатный полиспаст равна весу груза Qст.
Во втором случае нагружения предполагается, что груз лежит на опорном основании и канатный полиспаст не нагружен. Динамическая нагрузка возникает в период, когда к подъемному полиспасту и грузозахвату, движущемуся со скоростью подъема груза ![]() , будет приложен вес груза. При этом динамическая нагрузка будет:
, будет приложен вес груза. При этом динамическая нагрузка будет:
![]()
где k — жесткость опорной конструкции.
4.1. Подъем груза «с веса» (рис. 4.1)
В данном случае систему конструкции крана можно свести к двухмассовой, заменив жесткость канатов Kп и жесткость конструкции крана Кк приведенной жесткостью
К = Кп. Кк/(Кп + Кк).
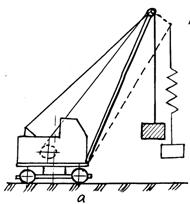
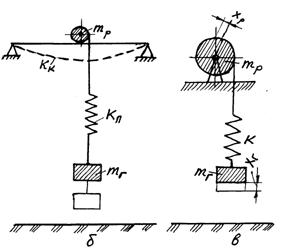
Рисунок 4.1 — Схемы динамического нагружения при подъеме груза «с веса»: а – в стреловом кране; б – в кране мостового типа; в — расчетная схема
Тогда упрощенную систему можно представить состоящей из двух масс: mр — массы ротора двигателя и приведенных к нему масс механизма подъема и mr — массы груза, связанных между собой упругим элементом с приведенной жесткостью k.
Для составления уравнений движения системы кран-груз применяем принцип Лагранжа, как наиболее универсальный. При перемещениях Xp массы mp и Xr массы mr кинетическая K и потенциальная П энергии составляют:
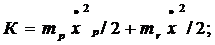
П=k(xp — xг)2/2.
Подставив данные выражения в уравнение Лагранжа, получим систему уравнений
(4.1)
где Тизб — избыточная сила двигателя.
Сделав в системе уравнений (4.1) несложные преобразования, получим уравнение в каноническом виде
(4.2)
где x = xp – xr; m = 1/mp+1/mr; p — круговая частота колебаний упругого звена.
Полное решение уравнения (4.2)
X = Qст + 2Tизб(1- cos pt) / (kmmp).
Максимальное усилие в упругом звене будет при cos pt = -1:
Pmax = k. x = Qст+ 2Tизб. mr/(mr+ mp).
4.2. Подъем груза «с подхватом» (рис.4.2)
В этом случае учитывают только жесткость конструкции крана Kk, т. е. массы крана mk и груза mr рассматривают как одну массу mк. г. (рис.4.2, в).
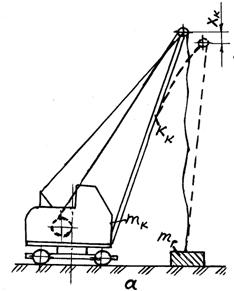
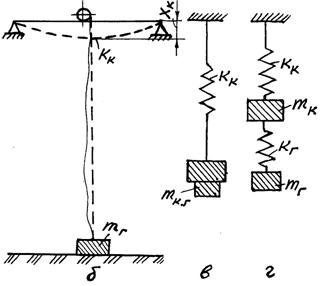
Рисунок 4.2 — Схема динамического нагружения при подъеме груза с подхватом: а — на стреловом кране; б — на кране мостового типа; в — расчетная схема одномассовой системы; г — то же, двухмассовой системы.
Применив принцип Лагранжа, получим уравнение движения
(4.3)
решение которого –![]()
где прогиб конструкции от статической нагрузки; скорость подъема груза; круговая частота свободных колебаний.
Максимальная динамическая сила, действующая на грузозахват, будет при sin pt = -1:
Основная литература [1, c. 237…245]
Дополнительная литература [10, c. 147…151]
Контрольные вопросы:
1. Как представляют упрощенную динамическую систему кран-груз при подъеме груза «с веса»?
2. Напишите выражение для максимального усилия в упругом звене при подъеме груза «с веса».
3. По какой зависимости определяют максимальную динамическую силу, действующую на грузозахват крана при подъеме груза «с подхватом»?
Лекция 5
Динамика механизмов передвижения кранов и тележек с гибким подвесом груза
Груз при работе грузоподъемной машины подвешен на канатах, поэтому наблюдается его раскачивание, которое вызывает неравномерное движение механизмов передвижения кранов или тележек, дополнительные нагрузки на элементы кранов и др. Поэтому необходимо уметь оценивать этот эффект колебаний груза при уточненных расчетах грузоподъемных машин.
Частоты маятниковых колебаний груза относительно крана (мостового, козлового и др.) существенно (в 6…10 раз) ниже частот упругих колебаний крановой металлоконструкции и трансмиссии механизма передвижения. Ввиду этого маятниковые колебания груза практически не зависят от упругих колебаний крана и их можно рассчитывать раздельно.
Для оценки гибкости подвеса груза и его влияния на динамику механизма передвижения примем в качестве расчетной схемы двухмассовую систему (рис.5.1, a)
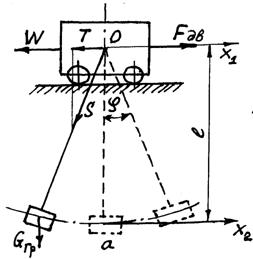
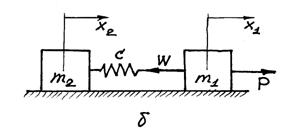
Рисунок 5.1 — Расчетные схемы механизмов передвижения с учетом гибкости подвеса груза: a — основная; b – приведенная
На рис. 5.1. обозначено:
m2 — масса груза; m1 — масса тележки или крана и механизма передвижения, приведенная к поступательному перемещению тележки или крана; x1 — горизонтальное перемещение массы m1; x2 – абсолютное горизонтальное перемещение груза; ![]() — угол отклонения подвески груза от вертикали;
— угол отклонения подвески груза от вертикали; ![]() — длина подвеса груза; W — сила сопротивления передвижению крана или тележки;
— длина подвеса груза; W — сила сопротивления передвижению крана или тележки; ![]() — движущее усилие, действующее на тележку или кран.
— движущее усилие, действующее на тележку или кран.


