Математическое выражение 2-го закона термодинамики

Энтропия изолированной ТС не изменяется только при равновесных процессах в ней и всегда возрастает при неравновесных процессах. Таким образом, 2-ой закон термодинамики – закон об энтропии и состоит из принципа существования энтропии и принципа возрастания энтропии.

Все равновесные процессы – обратимые, а неравновесные – необратимые процессы. Процесс называется необратимым, если суммарный запас энергии направленного, упорядоченного движения частиц ТС (работы) уменьшается, и обратимым, если этот запас энергии сохраняется. В необратимых процессах происходит диссипация (рассеяние) энергии упорядоченного движения материи в энергию теплового, неупорядоченного движения, которую нельзя превратить ни в какой другой вид энергии в обратном направлении. Обратимый (равновесный) процесс возможен только при бесконечно малых перепадах параметров на границе ТС и окружающей среды в любой момент процесса.

Второй закон термодинамики является обобщением опытных данных, указывает на особый характер протекания тепловых процессов и устанавливает пределы возможных превращений теплоты в работу. Этот закон позволяет определить направление и условия протекания любого термодинамического процесса. Дело в том, что тепловые процессы, удовлетворяющие первому закону термодинамики, подразделяются на самопроизвольные, протекающие без внешнего воздействия в данных условиях и на процессы, которые не могут происходить в данных условиях без внешнего воздействия.

В изолированной ТС самопроизвольные процессы протекают в направлении достижения равновесия системы. При этом работа преобразуется в теплоту (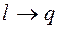), а теплота переходит лишь от тела с более высокой температурой к телу с более низкой температурой. Процессы с превращением теплоты в работу (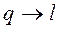) в изолированной системе самопроизвольно идти не могут. Открытие 2-го закона термодинамики было связано с анализом работы тепловых машин (Сади Карно).

Для осуществления процессов с превращением теплоты в работу надо создать из двух тел с различной температурой (Т1>Т2) неравновесную ТС, обладающую запасом энергии направленного упорядоченного движения частиц, а также осуществить с помощью термодинамического рабочего тела (ТРТ) обратимый цикл и передать результирующую работу цикла lц третьему телу – аккумулятору работы. При этом всю подведенную теплоту q1 нельзя превратить в работу lц. Часть теплоты необходимо отвести в холодильник .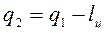

Схему превращения теплоты в работу можно представить в виде :

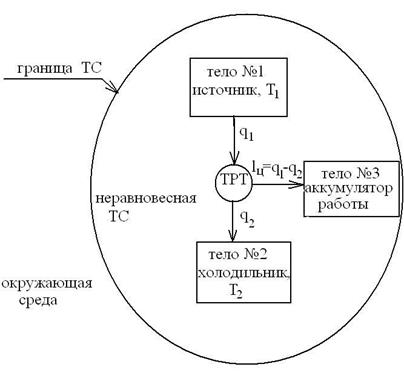
Неравноценность превращений работы в теплоту и теплоты в работу объясняется тем, что энергию направленного движения частиц (работу) можно превратить в тепловую энергию неупорядоченного, хаотического движения частиц, а обратный процесс возможен только при наличии соответствующей компенсации.

Наиболее краткой формулировкой 2-го закона термодинамики является формулировка Томсона-Кельвина: «Теплота, содержащаяся в окружающей среде, не может быть превращена в работу теплового двигателя, если температура всех окружающих тел будет одинаковой, т. е. вечный двигатель II рода неосуществим». Вечный двигатель II рода – это двигатель, который производил бы механическую работу исключительно за счет теплоты окружающей среды с одинаковой температурой во всех ее точках.

6.2. Математическое выражение 2-го закона термодинамики. Три составляющие изменения энтропии термодинамической системы

Энтропия равновесного процесса S — это функция состояния и ее дифференциал dS — полный дифференциал

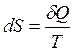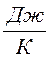, [] и , [].

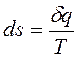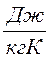Температура Т на границе ТС, где подводится теплота, есть интегрирующий делитель, превращающий неполный дифференциал – теплоту в полный дифференциал – энтропию. Для равновесного кругового процесса ∮∮ 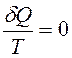— интеграл Клаузиуса.

У всякой ТС существует однозначная функция состояния – энтропия, которая при адиабатных равновесных процессах не изменяется.

Для сложной открытой ТС, которая взаимодействует с окружающей средой, изменение энтропии dS связано с подводом теплоты 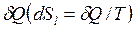, с протеканием процессов внутри ТС 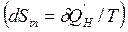и с подводом массы вещества :

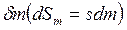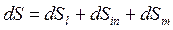, Дж/К.

Для процессов, протекающих внутри ТС, — «некомпенсируемая теплота» (Клаузиус), в которую превращается количество работы вследствие необратимости (неравновесности) процессов внутри системы.

Если границу ТС пересекают несколько веществ с массами mi , то изменение энтропии за счет ее подвода извне будет равно:

.

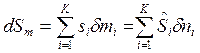Для обратимых процессов при подводе теплоты извне изменение энтропии ТС равно изменению энтропии окружающей среды с обратным знаком, т. е.

,

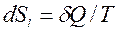а в случае необратимых процессов

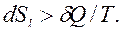
При протекании процессов внутри ТС энтропия может только расти, т. е. dSin>0.

При этом количество энергии упорядоченного движения частиц, которое диссипировало в тепловую энергию, равно: 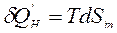. Тогда математическое выражение второго закона термодинамики для сложной открытой ТС примет вид:

,

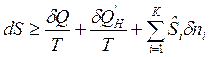где знак «=» для равновесных процессов, а знак «>» для неравновесных процессов.

Знак неравенства показывает, что изменение энтропии больше величины .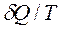

Для закрытой ТС dSm=0 и математическое выражение 2-го закона термодинамики будет иметь вид:

.

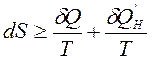Для неравновесного кругового процесса

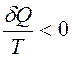∮, т. е. круговой интеграл по неравновесному пути не определяет изменение энтропии в круговом процессе (цикле), а меньше его. (Для равновесного кругового процесса ∮).

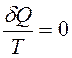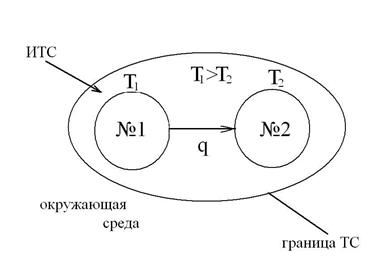
В качестве примера, характеризующего возрастание энтропии при неравновесных процессах, рассмотрим самопроизвольный переход теплоты от горячего тела №1 с температурой Т1 к холодному телу №2 с температурой Т2, приведя их в контакт и рассматривая систему из этих тел, как изолированную ТС, в соответствии со следующей схемой: